Cuadernillo de Apuntes de Matemáticas I Luis Ignacio

Cuadernillo de Apuntes de
Matemáticas I
Luis Ignacio Sandoval
Paéz
1
Índice
Números reales
1.1 Clasificación de los números reales.
1.2 Propiedades.
1.3Interpretación geométrica de los números reales.
1.4 Desigualdades lineales y cuadráticas y sus propiedades.
5
7
10
13
Funciones
2.1 Definición de función.
20
2.2 Representaciones de funciones(tablas, gráficas, formulas y palabras) 21
2.3.2 Función racional.
27
2.3.3 Función raíz.
29
2.3.4 Función exponencial.
31
2.3.5 Función logarítmica.
34
2.3.6 Función definida parte por parte.
37
2.3.7 Función inversa.
38
2.4 Clasificación de las funciones por sus propiedades:
39
2.4.1 Función creciente y decreciente
39
2.4.2 Función par e impar.
41
2.4.3 Función periódica.
42
2.5 Operaciones con funciones y composición de funciones
43
Límites y Continuidad
3.1 Definición de límite
3.2 Propiedades de los límites
3.3 Límites laterales
3.4 Asíntotas (verticales, horizontales u oblicuas)
3.5 Definición de continuidad.
3.6 Propiedades de la continuidad.
2
46
47
48
51
54
56
Derivadas
4.1 Definición de la derivada.
57
4.2 Interpretación geométrica y física de la derivada.
57
4.3 Derivada de la función constante, derivada del producto de una constante
n
por una función, derivada de la función x cuando n es un entero positivo, y
cuando n es un número real, derivada de una suma de funciones, derivada d
un producto de funciones y derivada de un cociente de funciones.
59
4.4 Derivada de las funciones exponenciales.
62
4.5 Derivada de las funciones trigonométricas.
63
4.6 Derivada de las funciones compuestas
66
(regla de la cadena).
4.7 Derivada de la función inversa.
69
4.8 Derivada de las funciones logarítmicas.
71
4.9 Derivada de las funciones trigonométricas inversas.
73
4.10 Derivada de las funciones implícitas.
79
4.11 Derivadas sucesivas.
83
4.12 Teorema del valor medio y teorema de Rolle.
86
Aplicaciones de la derivada
5.1 Recta tangente, normal e intersección de curvas.
5.2 Máximos y mínimos (criterio de la primera derivada).
5.3 Máximos y mínimos (criterio de la segunda derivada.)
5.4 Funciones crecientes y decrecientes.
5.5 Concavidades y puntos de inflexión.
5.6 Estudio general de curvas.
5.7 Derivada como razón de cambio y aplicaciones.
5.8 Regla de L`Hôpital.
3
93
95
99
101
104
110
113
115
Sucesiones y series
6.1 Definición de sucesión.
6.2 Límite de una sucesión.
6.3 Sucesiones monótonas y acotadas.
6.4 Definición de serie infinita.
6.5 Serie aritmética y geométrica.
6.6 Propiedades de las series.
6.7 Convergencia de series.
4
118
118
121
122
122
124
126
CAPÍTULO I: LOS
NÚMEROS
REALES.
NÚMEROS
REALES
1.1 Clasificación de los números reales.
En matemáticas, los números reales incluyen tanto a los números racionales
(como: 31, 37/22, 25,4) como a los números irracionales aquellos que no se
pueden expresar de manera fraccionaria y tienen infinitas cifras decimales no
periódicas, tales como:
expresión decimal.
. Números reales son aquellos que poseen una
Pueden ser descritos de varias formas, aparentemente simples, pero estas
carecen del rigor necesario para los propósitos formales de matemáticas.
Durante los siglos XVI y XVII el cálculo avanzó mucho aunque carecía de una
base rigurosa, puesto que en el momento no se consideraba necesario el
formalismo de la actualidad, usando expresiones como «pequeño», «límite»,
«se acerca» sin una definición precisa. Esto llevó finalmente a una serie de
paradojas y problemas lógicos que hicieron evidente la necesidad de crear una
base rigurosa a la nueva matemática, la cual incluyó definiciones formales y
rigurosas (aunque ciertamente técnicas) del concepto de número real.
5
Un número real puede ser un número racional o un número irracional. Los
números racionales son aquellos que pueden expresarse como el cociente de
dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los
irracionales son todos los demás. Los números racionales también pueden
describirse como aquellos cuya representación decimal es eventualmente
periódica, mientras que los irracionales tienen una expansión decimal
aperiódica:
Ejemplos
1/4 = 0,250000... Es un número racional puesto que es periódico a partir del
tercer número decimal.
5/7 = 0,7142857142857142857.... Es racional y tiene un período de longitud 6
(repite 714285).
es irracional y su expansión decimal
es aperiódica.
Otra forma de clasificar los números reales es en algebraicos y trascendentes.
Un número es algebraico si existe un polinomio que lo tiene por raíz y es
trascendente en caso contrario. Obviamente, todos los números racionales son
algebraicos: si es un número racional, con p entero y q natural, entonces es
raíz del binomio qx=p. Sin embargo, no se cumple el recíproco, no todos los
números algebraicos son racionales.
Ejemplos
El número
12x2 + 6x − 8
es algebraico puesto que es la raíz del polinomio 8x3 −
Un ejemplo de número trascendente es
Operaciones con números reales
Con números reales pueden realizarse todo tipo de operaciones básicas con
dos excepciones importantes:
1. No existen raíces de orden par (cuadradas, cuartas, sextas, etc.) de números
negativos en números reales, razón por la que existe el conjunto de los
números complejos donde estas operaciones sí están definidas.
2. No está definida la división entre cero, pues carece de sentido dividir entre
nada o entre nadie.
Estas dos restricciones tienen repercusiones importantes en ramas más
avanzadas de las matemáticas: existen asíntotas verticales en los lugares
6
donde una función se indefine, es decir, en aquellos valores de la variable en
los que se presenta una división entre cero, o no existe gráfica real en aquellos
valores de la variable en que resulten números negativos para raíces de orden
par, por mencionar un ejemplo de construcción de gráficas en geometría
analítica.
La principal característica del conjunto de los números reales es la completitud,
es decir, la existencia de límite para dada sucesión de Cauchy de números
reales.
Notación
Los números reales miden cantidades continuas que se expresan con
fracciones decimales que tienen una secuencia infinita de dígitos a la derecha
de la coma decimal, como por ejemplo 324,8232. Frecuentemente también se
subrepresentan con tres puntos consecutivos al final (324,823211247…), lo
que significaría que aún faltan más dígitos decimales, pero que se consideran
sin importancia.
Las medidas en las ciencias físicas son siempre una aproximación a un número
real. No sólo es más conciso escribirlos con forma de fracción decimal (es
decir, números racionales que pueden ser escritos como proporciones, con un
denominador exacto) sino que, en cualquier caso, cunde íntegramente el
concepto y significado del número real. En el análisis matemático los números
reales son objeto principal de estudio. Puede decirse que los números reales
son la herramienta de trabajo de las matemáticas de la continuidad, como el
cálculo y el análisis matemático, mientras que los números enteros lo son de
las matemáticas discretas, en las que está ausente la continuidad.
Los matemáticos usan el símbolo (o, de otra forma, , la letra "R" en negrita)
para representar el conjunto de todos los números reales.
La notación matemática
se refiere a un espacio de n dimensiones de los
números reales; por ejemplo, un valor
consiste de tres números reales y
determina un lugar en un espacio de tres dimensiones.
En matemática, la palabra "real" se usa como adjetivo, con el significado de
que el campo subyacente es el campo de los números reales. Por ejemplo,
matriz real, polinomio real, y Álgebra de Lie real.
1.2 Propiedades.
Cuando a este conjunto de símbolos que solemos llamar “Números reales”
les adicionamos las operaciones de suma (+) y multiplicación (*) usuales
creamos algo que se le llama CAMPO DE NÚMEROS REALES. Estas
operaciones deben cumplir y de hecho están caracterizadas con las siguientes
propiedades, las cuales mostramos en la tabla 1: donde a, b y c son números
reales cualesquiera:
7
Si a, b y c son números reales entonces:
Propiedad
Conmutativa
Propiedad
Asociativa
Operación
Suma
a+b = b+a
Multiplicación
ab = ba
Operación
Suma
Identidad
Suma
Inversos
Operación
Suma
Definición
Distributiva
Operación
Suma respecto a
8
Ejemplo
Puedes hacer
diferentes
asociaciones al
sumar o multiplicar
reales y no se
afecta el resultado.
7+(6+1)=(7+6)
+1
-2(4x7)= (2x4)7
Ejemplo
a+0=a
Todo real sumado a 0 se
queda igual; el 0 es la
identidad aditiva.
-11 + 0 = -11
a x 1= a
Todo real multiplicado
por 1 se queda igual; el 1
es la identidad
multiplicativa.
17 x 1 = 17
Definición
a + ( -a) = 0
Que dice
La suma de
opuestos es cero.
Ejemplo
15+ (-15) =
0
El producto de
recíprocos es 1.
Definición
a(b+c) = ab + ac
Multiplicación
Propiedad de los
opuestos
Que dice
Que dice
Multiplicación
Propiedad
2+8 = 8+2
5(-3) = ( -3)5
a(bc) = (ab)c
Operación
Ejemplo
El orden al sumar o
multiplicar reales no
afecta el resultado.
Definición
Multiplicación
Propiedad
Que dice
a+(b+c)=(a+b)+c
Multiplicación
Propiedad
Definición
Que dice
Que dice
El factor se
distribuye a cada
sumando.
Ejemplo
Ejemplo
2(x+8) =
2(x) + 2(8)
-( -a ) = a
El opuesto del
opuesto es el mismo
número.
-(-9)=9
(-a)( b)= a (-b)= (ab)
El producto de reales
con signos diferentes
es negativo.
( -15) (2) = 15( - 2) = - (15 x
2)
= - 30
( - a)( -b) = ab
El producto de reales
con signos iguales es
positivo.
( -34) ( - 8) = 34 x 8
-1 ( a ) = - a
El producto entre un
real y -1 es el opuesto
del número real.
-1 ( 7.6 ) = - 7.6
Propiedades del cero
Propiedad del cero
Que dice
Ejemplo
ax0=0
Todo real multiplicado
por 0 es 0.
16 x 0 = 0
a x b = 0 entonces
Si un producto es 0
entonces al menos uno
de sus factores es igual
a 0.
(a+b)(a-b) = 0
entonces
a=0ób=0
a+b=0óa–b=0
A las propiedades de ℝ enunciadas se les denomina “propiedades de
campo”, para distinguirlas de otros dos conjuntos de propiedades de este
conjunto llamadas propiedades de orden y propiedades de continuidad
Identifica la propiedad:
5 ( 4 x 1.2 ) = ( 5 x 4 ) 1.2
14 + ( -14 ) = 0
3 ( 8 + 11 ) = 3 ( 8) + 3 (11)
( 5 + 7 ) 9 = 9 (7 + 5)
9
Aplica la propiedad indicada:
5(x + 8) ; (conmutativa de suma)
(3 x 6) 2 ; (asociativa de multiplicación)
(9 + 11) + 0 ; (identidad aditiva)
12(x + y) ; (distributiva)
9(6 + 4) ; (conmutativa de multiplicación)
(x + y) + z ; (asociativa de suma)
1.3 Representación Geométrica de los Números Reales
Geométricamente podemos representar el conjunto de los números reales
mediante los puntos de una recta horizontal que llamaremos la recta real o el
eje real. Para ello, escogemos un punto de la recta para representar el número
0 y otro punto a la derecha de este para representar al número1. La longitud
del segmento determinado por los puntos marcados 0 y 1 se selecciona como
unidad de distancia. Utilizando esta unidad de distancia representamos los
números positivos a la derecha del 0 y los números negativos a la izquierda del
0. El entero positivo n se representa por el punto situado a una distancia de n
unidades a la derecha del 0 y el entero negativo –n se representa por el punto
situado a una distancia de n unidades a la izquierda del 0, como se indica en la
siguiente figura donde se representan los enteros entre -5 y 5.
En la práctica, se acostumbra a identificar un número real con el punto sobre la
recta que lo representa y, a utilizar como sinónimas las expresiones " el punto
" y " el número ".
Para representar la distancia entre dos puntos de la recta, necesitamos calcular
la diferencia entre la coordenada del punto que esta a la derecha y la
coordenada del punto que está a la izquierda. Si los puntos tienen coordenadas
y
, entonces cuando
la distancia es
y cuando
la
distancia es
, ya que la distancia es siempre positiva. Con el fin de tener
una única fórmula para calcular la distancia en todos los casos, introducimos la
noción de valor absoluto.
Definición: Si es un número real, su valor absoluto que notamos
definimos
| x| =
10
, lo
Ejemplo
, pues
, pues
, pues
, pues
De acuerdo con nuestra observación anterior, si
y
son las coordenadas de
dos puntos sobre una recta, la distancia entre ellos se define como
En particular,
.
representa la distancia del origen al punto .
La relación de orden entre números reales tiene una interpretación geométrica
muy simple:
si y sólo si el punto que representa
esta localizado a la izquierda del
punto que representa .
La representación geométrica es de gran utilidad en la resolución de problemas
y en la visualización de muchas propiedades importantes de los números
reales.
Se llama i nte r va l o al conj unto de núm e r os r e a le s comprendidos
entre otros dos dados: a y b que se llaman ex tr e m os del i nte rva l o.
Intervalo abierto
I nte r va l o a bi e r to, (a , b), es el c onjunto de todos l os núm e r os
r e a l es m a yor e s que a y m e nor e s que b.
(a , b) = { x
/ a < x < b}
Intervalo cerrado
11
I nte r va l o c e r r a do, [a , b], es el c onjunto de todos l os núm e r os
r e a l es m a yor e s o i gua l e s que a y m e nor e s o i gua l es que b.
[a , b] = { x
/ a ≤ x ≤ b}
I n t e rva lo sem ia b iert o p o r la izqu ie rd a
I n t e rva lo se m ia b iert o p o r la izqu ie rd a , (a , b ] , e s e l co nju n t o de
t o d o s lo s núm e ro s re a le s m a yo re s qu e a y m e no re s o igu a le s
qu e b.
(a , b] = { x
/ a < x≤ b}
I n t e rva lo sem ia b iert o p o r la d e re ch a
I n t e rva lo se m iab iert o p o r la d e re ch a, [ a , b ), e s e l co n ju n t o de
t o d o s lo s núm e ro s re a le s m a yo re s o igu a le s qu e a y m e no res
qu e b.
[a , b) = { x
/ a ≤ x < b}
Cu a n do qu e rem o s n o mb ra r un co n ju nt o de p u n to s f o rma d o p or
d o s o m á s d e e sto s in t e rva lo s, se u t iliza e l si gn o
(uni ón)
e n t re e llo s.
12
1.4 Desigualdades lineales y cuadráticas de los números reales.
Desigualdades o inecuaciones de primer grado con una incógnita
La expresión
a
b,
Quiere decir que "a" no es igual a "b". Según los valores particulares de "a" y
de "b", puede tenerse a > b, que se lee "a" mayor que "b", cuando la diferencia
a - b es positiva y a < b, que se lee "a" menor que "b", cuando la diferencia a - b
es negativa.
Desigualdad "es la expresión de dos cantidades tales que la una es mayor o
menor que la otra".
Lo mismo que en las igualdades, en toda desigualdad, los términos que están a
la izquierda del signo mayor o menor, forman el primer miembro de la
desigualdad, y los términos de la derecha, forman el segundo miembro. De la
definición de desigualdad, lo mismo que de la escala de los números
algebraicos, se deducen algunas consecuencias, a saber:
1º Todo número positivo es mayor que cero
2º Todo número negativo es menor que cero
3º Si dos números son negativos, es mayor el que tiene menor valor
absoluto;
Sentido de una desigualdad.
Los signos > o < determinan dos sentidos opuestos o contrarios en las
desigualdades, según que el primer miembro sea mayor o menor que el
13
segundo. Se dice que una desigualdad cambia de sentido, cuando el miembro
mayor se convierte en menor o viceversa.
Desigualdades absolutas y condicionales.
Así como hay igualdades absolutas, que son las identidades, e igualdades
condicionales, que son las ecuaciones; así también hay dos clases de
desigualdades: las absolutas y las condicionales.
Desigualdad absoluta es aquella que se verifica para cualquier valor que se
atribuya a las literales que figuran en ella
Ejemplo:
a2+ 3 > a
Desigualdades condicional es aquella que sólo se verifica para ciertos
valores de las literales:
Ejemplo:
2x - 8 > 0
que solamente satisface para x > 4. En tal caso se dice que 4 es el límite de x.
Las desigualdades condicionales se llaman inecuaciones.
Propiedades de las desigualdades.
1. Una desigualdad no cambia de sentido cuando se añade o se resta un
mismo número a cada miembro
Efectivamente si en la desigualdad a > b se designa por "c" lo que falta a "b"
para ser igual a "a", se tiene:
a=b+c
Añadiendo un mismo número, positivo o negativo a los miembros, se puede
escribir:
a+m=b+c+m
Suprimiendo "c" en el segundo miembro, resulta evidentemente
a + m > b +m
14
Ejemplos:
9>5
9+2>5+2
11 > 7
-2 > -6
-2 -3 > -6 -3
-5 > -9
Consecuencia de esta propiedad: Puede suprimirse un término en un miembro
de una desigualdad, teniendo cuidado de agregar en el otro miembro el término
simétrico del suprimido; es decir, se puede pasar un término de un miembro a
otro, cambiando su signo, porque esto equivale a sumar o restar una misma
cantidad
a
los
dos
miembros.
Ejemplo:
6x -2 > 4x + 4
6x -4x > 4 + 2
2. Una desigualdad no cambia de sentido cuando se multiplican sus dos
miembros por un mismo factor positivo, o se dividen entre un mismo divisor,
también positivo.
Sea
la
desigualdad
a
>
b,
es
decir,
a
=
b
+
c
Multiplicando ambos miembros de la desigualdad por un número positivo "m",
resulta:
am = bm + cm.
Suprimiendo el término positivo "cm", en el segundo miembro disminuye, y se
tiene:
am > bm
Si "m" es recíproco de un número positivo, queda evidenciada la segunda parte
de
esta
propiedad
Ejemplos:
12 > 7
12 * 3 > 7 * 3
36 > 21
15 > -25
15 ÷ 5 >(-25) ÷ 5
3 > -5
3. Una desigualdad cambia de sentido cuando se multiplican sus dos
miembros por un mismo factor negativo, o se dividen entre un mismo divisor,
también negativo.
Sea
la
desigualdad
a
>
b,
es
decir,
a
=
b
+
c
Multiplicando ambos miembros de la desigualdad por el factor negativo -n se
obtiene:
15
-an = -bn -cn
Suprimiendo -cn, en el segundo miembro aumenta; por tanto,
-an < -bn
Si -n es recíproco de un número negativo, queda demostrada la segunda parte
del
enunciado.
Ejemplos:
3 > -15
3(-4) < (-15)(-4)
-12 < 60
64 < 80
64 ÷ (-4) >80 ÷ (-4)
-16 > -20
Consecuencia de la propiedad anterior pueden cambiarse todos los signos de
una desigualdad, con tal que se cambie el sentido de la misma; porque esto
equivale
a
multiplicar
sus
dos
miembros
por
-1.
Ejemplo:
-7x + 130 < 9 -5x
7x - 130 > -9 + 5x
4. Si los dos miembros de una desigualdad son positivos y se elevan a la
misma potencia, la desigualdad no cambia de sentido.
Sea la desigualdad a < b, en la que "a" y "b" son positivos. Multiplicando sus
dos miembros por "b", resulta:
ab < b2
En el primer de esta desigualdad, sustituyendo "b" por "a", la desigualdad se
refuerza; por tanto:
a2 < b2
Ejemplo:
7 < 10
73 < 103
343 < 1000
5. Si los dos miembros de una desigualdad son negativos y se elevan a una
potencia de grado impar, no cambia el sentido de la desigualdad; pero hay
cambio de sentido si el grado de la potencia es par.
16
Sea la desigualdad -a < -b
a) Multiplicando sus dos miembros por b2 se obtiene:
-ab2 < -b3
En el primer miembro, reemplazando b2 por a2, la desigualdad se refuerza;
luego se puede escribir:
-a3 < -b3
b) Multiplicando los dos miembros de la primera desigualdad por -b y haciendo
análogas transformaciones, la desigualdad cambia de sentido, porque sus
términos cambian de signo, y se tiene:
a2 > b2
Ejemplos:
-3 > -6
(-3)3 > (-6)3
-27 > -216
-8 < -4
(-8)2 > (-4)2
64 > 16
6. Si se suman miembro a miembro varias desigualdades de mismo sentido,
resulta una desigualdad de mismo sentido que aquéllas.
Sean las desigualdades a > b; a' > b'; a" > b"
Se puede escribir:
a=b+c
a' = b' + c'
a" = b" + c"
Sumando miembro a miembro y suprimiendo c + c' + c", se tiene,
sucesivamente:
a + a' + a" = b + b' + b" + c + c' + c"
a + a' + a" > b + b' + b"
Ejemplo:
Dado: 2x > 10 y 7x > 26
se obtiene: 9x > 36
7. Si se restan miembro a miembro dos desigualdades de sentido contrario,
resulta una desigualdad de igual sentido que el minuendo.
Sean las desigualdades a > b y c < d
Invirtiendo la segunda desigualdad y sumándola a la primera se tiene
17
a>b
d>c
a + d > b +c
Restando d + c de cada miembro, resulta:
a - c > b -d
Ejemplo:
Dado: 7x < 12 y 5x > 16,
se obtiene: 2x < -4
Las desigualdades lineales se resuelven exactamente como las igualdades,
con una importante excepción: al multiplicar o dividir por una cantidad negativa,
el signo de desigualdad se invierte.
El conjunto solución lo escribimos así: S = ]-¥, -13/7]
Desigualdades Cuadráticas
1 Factorizables
Ejemplo 1: Hallar el conjunto solución de x2 - 6x + 8 > 0.
Solución:
Factorizando, (x - 2)(x - 4) > 0.
Gráficamente:
\ x < 2 o x > 4.
El conjunto solución es
{x Î R : x < 2 o x > 4}
18
Recta Numérica:
\ x < 2 o x > 4.
El conjunto solución es
{x Î R : x < 2 o x > 4}
Ejemplo 2: Hallar el conjunto solución de (2x - 1)(x + 2) < x(4 + x).
Solución:
2x2 + 3x - 2 < 4x + x2
x2 - x - 2 < 0
(x + 1)(x - 2) < 0
\ -1 < x < 2.
El conjunto solución es
{x Î R : -1 < x < 2}
2 No Factorizable
Ejemplo 3: Resolver x2 - 4x + 1 > 0.
Solution:
Método 1: Completando el Cuadrado
x2 - 4x + 1 = x2 - 4x + 4 - 3
= (x - 2)2 - 3
(x - 2)2 - 3 > 0
(x - 2)2 > 3
|x - 2| > Ö3
x - 2 > Ö3 o x - 2 < -Ö3
x > 2 + Ö3 o x < 2 - Ö3
19
CAPÍTULO II:
FUNCIONES.
2.1 Definición de función.
Existen diferentes tipos de expresiones algebraicas, sin embargo algunas de
las expresiones que más nos interesan dentro del cálculo son las funciones.
Una función es una regla de asociación que relaciona dos o más conjuntos
entre sí; generalmente cuando tenemos la asociación dos conjuntos las función
se define como una regla de asociación entre un conjunto llamado dominio con
uno llamado codominio, también dominio e imagen respectivamente o dominio
y rango. Esta regla de asociación no permite relacionar un mismo elemento
del dominio con dos elementos del codominio.
Definición de función que se ampara bajo una regla de asociación de elementos del dominio
con elementos del codominio, imponiendo la restricción de relacionar un elemento del dominio
con uno del codominio, sin importar si los elementos del codominio puedan estar relacionados
con dos o más del codominio.
Donde se dice que f: A → B (f es una función de A en B, o f es una función
que toma elementos del dominio A y los aplica sobre otro llamado codominio B)
Se dice que el dominio de una función son todos los valores que puede tomar
el conjunto del dominio y que encuentra correspondencia en el conjunto
llamado codominio, generalmente cuando se habla del plano, el dominio es el
intervalo de valores que están sobre el eje de las X´s y que nos generan una
asociación en el eje de las Y´s.
20
El otro conjunto que interviene en la definición es el conjunto llamado
codominio o rango de la función, en ocasiones llamado imagen, este
conjunto es la gama de valores que puede tomar la función; en el caso del
plano son todos los valores que puede tomar la función o valores en el eje de
las Y´s.
También, cuando se grafica en el plano cartesiano se tiene una relación de dos
variables, considerando como variable aquella literal que está sujeta a los
valores que puede tomar la otra.
VARIABLES DEPENDIENTES.
Son aquellas variables que como su nombre lo indica, dependen del valor que
toma las otras variables Por ejemplo: f(x)= x, y o f(x) es la variable dependiente
ya que está sujeta a los valores que se le subministre a x.
VARIABLE INDEPENDIENTE.
Es aquella variable que no depende de ninguna otra variable, en el ejemplo
anterior la x es la variable independiente ya que la y es la que depende de los
valores de x.
VARIABLE CONSTANTE.
Es aquella que no está en función de ninguna variable y siempre tiene el mismo
valor ejemplo:
Y=2, la constante gravitacional, entre otras.
2.2 Representaciones de funciones(tablas, gráficas, formulas y palabras)
La gráfica de una función solo puede ser cortada por una recta vertical en un
punto, si dicha recta corta más de una punto no lo es. Como se muestra en la
figura
Se traza una línea paralela
Y debe de cortar una solo punto,
Y si corta dos o más puntos
No es función.
21
Se llama función polinómica de grado cero o función matemática constante
a la que no depende de ninguna variable, se la representa de la forma:
Donde a es la constante.
Como se puede ver es una recta horizontal en el plano xy, en la gráfica la
hemos representado en el plano, pero, como se puede ver la función no
depende de x, si hacemos:
Tenemos:
Donde a tiene un valor constante, en la gráfica tenemos representadas:
La función constante como un polinomio en x
Si un polinomio general, se supone que tiene la forma:
Una función constante cumple esta expresión con n= 0, es un polinomio de
grado 0.
22
Que es lo mismo que:
Que corresponde al termino independiente del polinomio.
2.3 Clasificación de las funciones por su naturaleza; algebraicas y
trascendentes.
2.3.1 Función polinomial.
Una variable es un símbolo al que se le puede asignar un conjunto de valores.
En general se representan las variables con las últimas letras del alfabeto:
u,v,w,x,y,z.
Una constante es un símbolo al que se le puede asignar un solo valor.
En general se representan las constantes con las primeras letras del alfabeto:
a, b, c.
Llamaremos función lineal a una ecuación del tipo
y = mx +b
Halle las expresiones que determinan las siguientes rectas y grafique.
Una recta de pendiente dos que pasa por el punto tres, cuatro.
Una función lineal que pasa por el punto P, de coordenadas (18.1;3) y el J de
coordenadas (1.2;-3.2)
Una recta con m igual a -2/5 y término independiente igual a cinco.
Determine todos los puntos de intersección entre estas tres rectas.
Responda las siguientes cuestiones y grafique.
Si y = (3/2 )x + 3x, determine el valor de b.
Si y = 3 + (1/2 )x, determine el valor de m
Si t= 2/5 + x + 3, determine el valor de m y b
Recuerde que:
23
Son paralelas si y solo si:
son perpendiculares si y solo si:
Funcione cuadrática
Decimos que una función es cuadrática si se puede expresar de la forma
f(x)= ax2+bx+c
donde a,b y c son constantes y a # 0
La gráfica de una función cuadrática es una parábola y su dominio es el
conjunto de los números reales.
Si a>0, se dice que la parábola es positiva y, en este caso, abre hacia arriba. Si
a<0, la parábola es negativa y abre hacia abajo.
A continuación se muestran tres funciones cuadráticas con sus respectivas
gráficas y una lista de algunas de las parejas ordenadas que pertenecen a
dichas funciones cuadráticas.
f(x)= x2 - 5x + 4
24
f(x)= - x2 - 5x + 4
f(x)= - 2x2 - 5x + 4
x
f(x)
x
f(x)
x
f(x)
0
4
-6
-2
-5/2
4
1
0
-5
4
-2
6
2
-2
-1
8
-1
7
4
0
0
4
0
4
5
4
1
-2
1
3
Funciones polinomiales
Si una función f está definida por
f ( x) = a n x n + a n −1 x n −1 + a n − 2 x n − 2 + ... + a1 x + a 0
donde a 0 , a1 ,..., a n son números reales ( a n ≠ 0 ) y n es un entero no negativo,
entonces, f se llama una función polinomial de grado n. Por lo tanto,
f ( x) = 3 x 5 − x 2 + 7 x − 1 , es una función polinomial de grado 5. Una función lineal
es una función polinomial de grado 1, si el grado de una función polinomial es
2, se llama función cuadrática, y si el grado es 3 se llama función cúbica. Una
función que puede expresarse como el cociente de dos funciones polinomiales
f ( x)
se llama función racional. Una función algebraica es aquella que
Q( x) =
g ( x)
está formada por un número finito de operaciones algebraicas sobre la función
identidad y la función constante. Las funciones trascendentes son las
trigonométricas, exponenciales y logarítmicas.
Ejemplos:
1. Para la función f ( x) = x 3 − 2 x 2 − 5 x + 6 :
(a) Determine el dominio de la función
(b) Las intercepciones con los ejes
(c) Elabora una tabla para algunos valores del Df
(d) Traza la gráfica de la función
(e) Estima una aproximación del Rf (puedes comprobarlo utilizando un
software)
Solución:
(a) D f = R (el dominio de las funciones polinomiales son todos los números
reales.
(b) Intercepciones con los ejes:
Si x = 0
y=6
La curva intercepta al eje y en el punto (0, 6)
25
Si y = 0
0 = x 3 − 2 x 2 − 5x + 6
Por división sintética:
Los factores de 6 son: ± 1, ± 2, ± 3, ± 6
1
-2
-5
6
1
-1
-6
1 1 un factor
-1 de
-6 la forma
0
Por lo tanto, f tiene
x-1.
f ( x) = x 3 − 2 x 2 − 5 x + 6 = ( x − 1) ( x 2 − x − 6)
El factor x 2 − x − 6 , puede descomponerse en:
x 2 − x − 6 = ( x − 3) ( x + 2)
Finalmente:
Si y = 0
x 3 − 2 x 2 − 5x + 6 = 0
( x − 1) ( x − 3) ( x + 2) = 0
Los valores de x son:
x −1 = 0
x−3= 0
x+2=0
⇒ x =1
⇒ x=3
⇒ x = −2
La curva corta al eje x en los puntos: (-2, 0), (1, 0) y (3, 0)
(c) La siguiente tabla será de mucha utilidad para graficar:
x
-4
-3
-2
-1
0
1
2
3
4
y
-70
-24
0
8
6
0
-4
0
18
(d) La función ha sido graficada utilizando un software:
26
10
y
y = x^3-2x^2-5x+6
8
6
4
2
x
-14
-12
-10
-8
-6
-4
-2
2
4
6
8
10
12
14
-2
-4
-6
-8
-10
(e) El recorrido de la función coincide con el contradominio:
Rf = R
2.3.2 Función racional
Definición: Si P(x) y Q(x) son polinomios, la función de la forma:
P( x )
f ( x) =
Q( x )
se llama una función racional, donde Q(x) es diferente de cero.
Ejemplos:
1
x−3
f ( x) = , g( x) =
, h( x ) = 3x 2 − 1
x
x +1
El dominio de las funciones racionales es el conjunto de todos los números
reales tal que el denominador sea diferente de cero.
Teorema: Sea f una función racional definida de la forma:
P( x )
f ( x) =
Q( x )
Donde P(x) y Q(x) son polinomios. Si a es un número real que Q(a) = 0 y
P(a) es diferente de cero, entonces la recta x = a es una asíntota vertical
de la gráfica de y = f(x).
Ejemplos para discusión: Halla las asíntotas verticales para cada de las
siguientes funciones:
27
1) f ( x ) =
1
x
2
x +1
2x − 3
3)h( x ) = 2
x −4
1
4) f ( x ) =
2x − 1
2) g ( x ) =
Teorema: Sea f una función racional definida por el cociente de dos
polinomios,
a x m +...+ a1 x + a 0
f ( x) = m n
bn x +...+b1 x + b0
entonces:
1) Para m < n, la recta y = 0 (el eje x) es una asíntota horizontal.
2) Para m = n, la recta y = am/bn, es una asíntota horizontal.
3) Para m > n, no hay asíntotas horizontales.
Halla las asíntotas horizontales para cada una de las siguientes funciones:
1) f ( x ) =
1
x
2
x +1
2x − 3
3)h( x ) =
3x + 1
3x 3
4) f ( x ) = 2
x +1
2) g ( x ) =
Gráfica de funciones racionales
Ahora utilizaremos las técnicas de interceptos y asíntotas para graficar algunas
funciones racionales.
Ejemplos para discusión: Dibuja la gráfica de:
28
1) f ( x) =
1
x
1
x +1
2x
3)h( x) =
x−3
3
4) f ( x) = 2
x −1
3x + 6
5) g ( x) =
x −1
2) g ( x) =
Teorema: Si f es una función definida de la forma:
P( x )
f ( x) =
Q( x )
Donde P(x) y Q(x) son polinomios y el grado de P(x) es 1 más que el grado de
Q(x), entonces se puede expresar de la forma:
r ( x)
f ( x ) = mx + b +
Q( x )
Donde el grado de r(x) es menor que el grado de Q(x). La recta y = mx + b es
una asíntota oblicua para la gráfica de f.
2.3.3 Función raíz
Sea n un número natural no nulo. La función (potenciación) x → x n define una
biyección de hacia si ''n'' es impar, y hacia
si ''n'' es par.
Se llama enésima raíz, o raíz de orden n su función matemática recíproca, y
se puede anotar de formas:
.
Para todo n natural, a y b reales positivos, tenemos la equivalencia:
.
En él, se han dibujado las curvas de algunas raíces, así como de sus funciones
recíprocas, en el intervalo [0;1]. La diagonal de ecuación y = x es eje de
simetría entre cada curva y la curva de su recíproca.
29
Cambiando de escala:
La raíz de orden dos se llama raíz cuadrada y, por ser la más frecuente, se
escribe
sin
superíndice:
La raíz de orden tres se llama raíz cúbica.
en
vez
de
.
El cálculo efectivo de la raíz se hace mediante las funciones logaritmo y
exponencial:
.
Todos los ordenadores y calculadoras emplean este método. El problema es
que éste cálculo no funciona con los números negativos, porque el logaritmo
usual sólo está definido en (0,+∞). De ahí una tendencia, todavía minoritaria,
30
de restringir la definición de las raíces de orden impar
números positivos.
a los
Propiedades
Como se indica con la igualdad
, la radicación es en
realidad otra forma de expresar una potenciación: la raíz de un cierto orden de
un número es equivalente a elevar a dicho número a la potencia inversa.
Por esto, las propiedades de la potenciación se cumplen también con la
radicación.
2.3.4 Función exponencial
Comenzaremos observando las siguientes funciones: f(x) = x2 y g(x) = 2x.
Las funciones f y g no son iguales. La función f(x) = x2 es una función que
tiene una variable elevada a un exponente constante. Es una función
cuadrática que fue estudiada anteriormente. La función g(x) = 2x es una función
con una base constante elevada a una variable. Esta es un nuevo tipo de
función llamada función exponencial.
Definición: Una función exponencial con base b es una función de la forma
f(x) = bx , donde b y x son números reales tal que b > 0 y b es diferente de
uno.
El dominio es el conjunto de todos los números reales y el recorrido es el
conjunto de todos los números reales positivos.
1) f(x) = 2x
8
6
4
2
0
-4
x
 1
2 ) f ( x ) =   = 2 −1
 2
31
( )
x
= 2−x
-2
0
2
4
8
6
4
2
0
-4
-2
0
2
4
Propiedades de f(x) = bx, b>0, b diferente de uno:
1) Todas las gráficas intersecan en el punto (0,1).
2) Todas las gráficas son continuas, sin huecos o saltos.
3) El eje de x es la asíntota horizontal.
4) Si b > 1 (b, base), entonces bx aumenta conforme aumenta x.
5) Si 0 < b < 1, entonces bx disminuye conforme aumenta x.
6) La función f es una función uno a uno.
Propiedades de las funciones exponenciales: Para a y b positivos, donde
a y b son diferentes de uno y x, y reales:
1) Leyes de los exponentes:
a )(a x )(a y ) = a x + y
b)
ax
= a x− y
ay
( )
c) a x
y
= a xy
d )(ab) x = a x b x
x
ax
 a
e)   = x
 b
b
2) ax = ay si y sólo si x = y
3) Para x diferente de cero, entonces ax = bx si y sólo si a = b.
Usa las propiedades para hallar el valor de x en las siguientes ecuaciones:
1) 2x = 8
2) 10x = 100
3) 4 x - 3 = 8
32
4) 5 2 - x = 125
Halla el valor de x:
1) 2x = 64
2) 27 x + 1 = 9
La función exponencial de base e
Al igual que π, e es un número irracional donde e = 2.71828... La notación e
para este número fue dada por Leonhard Euler (1727).
Definición: Para un número real x, la ecuación f(x) = ex define a la función
exponencial de base e.
Las calculadoras científicas y gráficas contienen una tecla para la función f(x) =
ex.
La gráfica de f(x) = ex es:
25
20
15
10
5
0
-4
-2
0
2
4
El dominio es el conjunto de los números reales y el rango es el conjunto de
los números reales positivos.
La función f(x) = ex es una función exponencial natural. Como 2<e<3, la
gráfica de
f(x) = ex está entre f(x) = 2x y f(x) = 3x, como se ilustra a continuación:
30
25
20
15
10
5
0
-4
33
-2
0
2
4
En la simplificación de expresiones exponenciales y en las ecuaciones
exponenciales con base e usamos las mismas propiedades de las ecuaciones
exponenciales con base b.
Simplifica:
( )
1) e 2 x
4x
=
3x
2)
e
=
e 3 x −8
Halla el valor de x en e x + 1 = e 3x - 1
1) Simplifica: (e 3x + 1) (e 2x – 5)
2) Halla el valor de x en e3x – 4 = e2x
La gráfica de la función exponencial f(x) = e-x es:
25
20
15
10
5
0
-4
-2
0
2
4
2.3.5 Función logarítmica
Las inversas de las funciones exponenciales se llaman funciones
logarítmicas. Como la notación f-1 se utiliza para denotar una función inversa,
entonces se utiliza otra notación para este tipo de inversas. Si f(x) = bx, en
lugar de usar la notación f-1(x), se escribe logb (x) para la inversa de la función
con base b. Leemos la notación logb(x) como el “logaritmo de x con base b”,
y llamamos a la expresión logb(x) un logaritmo.
Definición: El logaritmo de un número y es el exponente al cual hay que
elevar la base b para obtener a y. Esto es, si b > 0 y b es diferente de
cero, entonces
logb y = x si y sólo si y = bx.
34
Nota: La notación logb y = x se lee “el logaritmo de y en la base b es x”.
Ejemplos:
1) ¿A qué exponente hay que elevar la base 5 para obtener 25? Al exponente
2, ya que 52 = 25. Decimos que “el logaritmo de 25 en la base 5 es 2”.
Simbólicamente lo expresamos de la forma log5 25 = 2. De manera que, log5
25 = 2 es equivalente a 52 = 25. (Observa que un logaritmo es un
exponente.)
2) También podemos decir que 23 = 8 es equivalente a log2 8 = 3.
Nota: El dominio de una función logaritmo es el conjunto de todos los números
reales positivos y el recorrido el conjunto de todos los números reales. De
manera que, log10 3 está definido, pero el log10 0 y log10 (-5) no lo están. Esto
es, 3 es un valor del dominio logarítmico, pero 0 y -5 no lo son.
Expresa los siguientes logaritmos en forma exponencial:
1) log 3 9 = 2
2) log 49 7 =
1
2
 1
3) log 2   = −2
 4
Ejercicios:
1) Halla el valor de x si log3 9 = x.
2) Halla el valor de b si logb 8 = 3.
3) Halla el valor de y si log2 y = 7.
Ejercicio:
1) Halla el valor de y si log3 27 = y.
2) Halla el valor de b si logb 100 = 2.
3) Halla el valor de x si log2 x = -3.
Propiedades de las funciones logarítmicas: Si b, M y N son números reales
positivos, b es diferente de uno, y p y x son números reales, entonces:
1) logb 1 = 0
2) logb b = 1
3) logb bx = x
35
4) logb MN = logb M + logb N
5) log b
M
= log b M − log b N
N
6) logb Mp = p logb M
7) logb M = logb N si y sólo si M = N
Logaritmos comunes y naturales
Los logaritmos comunes son los logaritmos de base 10. Los logaritmos
naturales son los logaritmos de base e. Si y = ex entonces x = loge y = ln.
Muchas calculadoras tienen la tecla [log] para los logaritmos comunes y la
tecla [ln] para los logaritmos naturales.
Notación:
Logaritmo común: log x = log10 x
Logaritmo natural:
ln x = loge x
El logaritmo natural tiene todas las propiedades para los logaritmos con base b.
En particular:
1) ln e = 1
2) ln 1 = 0
3) ln(uv ) = ln u + ln v
u
= ln u − ln v
v
5) ln u n = n ln u
4) ln
Usa las propiedades para expandir:
2x − 1
=
x−2
2) ln 3 x 2 y =
1) ln
Gráficas de funciones logarítmicas
Las funciones y = bx y y = logb x para b>0 y b diferente de uno son funciones
inversas. Así que la gráfica de y = logb x es una reflexión sobre la recta y = x
de la gráfica de y = bx. La gráfica de y = bx tiene como asíntota horizontal al
eje de x mientras que la gráfica de y = logb x tiene al eje de y como asíntota
vertical.
36
Ejemplo:
8
3
6
2
1
4
0
-1 0
2
-2
4
6
8
-2
0
-4
2
0
2
4
y = 2x
-3
y = log2 x
Las funciones y = 2x y y = log2 x son funciones inversas una de la otra, por
tanto, la gráfica de y = log2 x es una reflexión de la gráfica de y = 2x sobre la
recta y = x. El dominio de y = 2x es el conjunto de los números reales y el
recorrido es todos los números reales mayores que cero. El dominio de y =
log2 x es el conjunto de los números reales mayores que cero y el recorrido el
conjunto de los números reales.
2.3.6 Función definida parte por parte
Trazar la gráfica de la función f si
Solución
Si x < 0, entonces f(x) = 2x +3, y la gráfica de f coincide con la recta y = 2x + 3.
Con esto se obtiene la parte de la gráfica que está a la izquierda del eje y, que
se ve en la Fig. 3.53. El circulo pequeño indica que el punto (0, 3) no está en la
gráfica.
Si 0 £ x < 2, se usa x2 para calcular valores de f y, por consiguiente, esta parte
de la gráfica de f coincide con la parábola y = x2, como se ve en la figura.
Nótese que el punto (2, 4) no pertenece a la gráfica.
Finalmente, si x ³ 2, los valores de f siempre son 1. Así, la gráfica de f para x ³ 2
es la media recta horizontal que se ve en la figura.
37
2.3.7 Función inversa
S e llam a func i ón i nve r s a o r e c i pr oc a de f a otr a func i ón f − 1
qu e c u mp le qu e:
S i f(a ) = b, e ntonc e s f − 1 (b) = a .
P o d emo s o b se rva r qu e :
E l d om in io d e f − 1 es e l re co rrid o d e f .
E l re c o rrid o de f − 1 e s e l do m in io de f .
S i qu e re mo s h a llar e l re c o rrid o d e u n a f un ció n t en em o s qu e
h a lla r e l do m in io de su f u n ción in ve rsa .
S i d o s func i one s so n i nve r s a s su c om pos i c i ón e s la func i ón
i de nti da d .
f o f
-1
= f
-1
o f = x
L a s grá f ica s d e f y f - 1 so n simé t rica s re sp e ct o d e la
b is e ct riz d e l p rim er y t e rce r cu a d ra nte .
38
Ha y qu e d ist in gu i r e n t re la func i ón i n ve r s a, f − 1 (x), y la
i nve r s a de una func i ón,
.
Cá lc u lo d e la f u n ció n in ve rsa
S e e s c rib e la e cu ació n de la f u n ción co n x e y.
S e de s p e ja la va ria b le x e n f u n ción d e la va ria b le y.
S e in te rca mb ia n las va ria b le s.
Ca lc u la r la func i ón i nve r s a d e :
2.4 Clasificación de las funciones por sus propiedades:
2.4.1 Función creciente y decreciente
Función estrictamente creciente en un intervalo
39
Una función
es estrictamente creciente en un intervalo
dos valores cualesquiera del intervalo,
y , se cumple que:
, si para
Cuando en la gráfica de una función estrictamente creciente nos movemos
hacia la derecha también nos movemos hacia arriba:
Una función es estrictamente creciente en el punto de abscisa
si
existe algún número positivo tal que es estrictamente creciente en el
intervalo
.
De esta definición se deduce que si es derivable en
y es
estrictamente creciente en el punto de abscisa
, entonces
.
Función creciente en un intervalo
Una función
es creciente en un intervalo
cualesquiera del intervalo,
y , se cumple que:
, si para dos valores
Función estrictamente decreciente en un intervalo
Una función
es estrictamente decreciente en un intervalo
dos valores cualesquiera del intervalo,
y , se cumple que:
40
, si para
Cuando en la gráfica de una función estrictamente decreciente nos movemos
hacia la derecha también nos movemos hacia abajo:
Una función
es estrictamente decreciente en el punto de abscisa
si
existe algún número positivo
tal que
es estrictamente decreciente en el
intervalo
.
De esta definición se deduce que si es derivable en
estrictamente decreciente en el punto de abscisa
y es
, entonces
.
Función decreciente en un intervalo
Una función
es decreciente en un intervalo
cualesquiera del intervalo,
y , se cumple que:
, si para dos valores
2.4.2 Función par e impar
SIMETRÍA.
FUNCIÓN PAR. Si una función f satisface que f(-x) = f(x) para todo x en su
dominio, entonces f es una función par.
Ejemplo. Comprobar que f(x) = x2 es par.
f(-x) = (-x)2 = x2 = f(x)
Como f(-x) = f(x), entonces la función es par!
f (-x)
-x
41
f (x)
x
La gráfica de una función par es simétrica respecto al eje y.
FUNCIÓN IMPAR. Si una función f satisface que f(-x) = - f(x) para todo x en su
dominio, entonces f es una función impar.
Ejemplo. Demostrar que f(x) = x3 es una función impar.
f(-x) = (-x)3 = - x3 = - f(x)
Como f(-x) = - f(x), entonces la función es impar!
f (x)
-x
x
f (-x)
La gráfica de una función impar es simétrica respecto al origen.
Ejemplos. Determine si cada una de las siguientes funciones es par, impar o
ninguno de los dos.
f(x) = x5 + x
f(x) = 1 – x4
f(x) = 2 x – x2
2.4.3 Función periódica
Un a f u n ción f (x) e s p e rió d ica , d e p e río d o T, si p a ra t o do
n ú me ro e n t e ro z, se ve rif ica :
f(x ) = f(x + zT)
L a f u n ció n f (x) = se n x e s p e riód ica d e p e riod o 2 π, ya qu e
c u m p le qu e :
se n (x + 2 π) = se n x
42
L a f un ció n f (x) = t g x e s p e rió d ica πd, eyapequ
rioed o
c u m p le qu e :
tg (x + π ) = tg x
2.5 Operaciones con funciones y composición de funciones
S i t e n em o s d o s f un cio n e s: f (x) y g( x), d e m o do qu e e l d o m in io
d e la 2 ª e st é in cluid o e n e l re co rrid o d e la 1 ª, se p u e de d ef in ir
u n a nu e va f u n ción qu e a so cie a ca da e le me n to d e l dom in io de
f (x) e l va lo r d e g[ f (x)] .
(g o f) (x ) = g [f(x )] = g (2 x ) = 3 (2 x ) +1 = 6 x + 1
(g o f ) (1 ) = 6 · 1 + 1 = 7
Do m in io :
D (g
o f)
= {x
D f / f(x )
Dg}
P r opi e da des
A s o c ia t iva :
f o (g o h) = (f o g ) o h
43
No e s c on mu t at iva .
f o g≠ g o f
E l e lem e n to ne u t ro e s la func i ón i denti da d, i (x ) = x.
f o i = i o f = f
S e a n la s f u n cion es:
44
45
CAPÍTULO III:
LÍMITES Y
CONTINUIDAD.
3.1 Definición de límite
Definición de límite
Sea f una función definida en una vecindad del punto (b,0).
Definición:
Se dice que
, si para cada número positivo , por pequeño que este
sea, es posible determinar un número positivo , tal que para todos los valores
de
, diferentes de , que satisfacen la desigualdad
desigualdad
Luego,
.
si y solo si para cada
entonces
tal que si
.
En forma gráfica se tiene:
46
, se verificará la
para cada
existe
tal que si
entonces
,
También el
desigualdad
puede interpretarse de la forma siguiente: como la
se deduce que
, entonces todos los puntos en
, que corresponden a los puntos
la gráfica de la función con ecuación
que se localizan a una distancia no mayor que del punto , se encontrarán
dentro de una franja de ancho
,limitada por las rectas
como se muestra en la siguiente figura:
,
Puede decirse entonces que la definición de límite dada anteriormente ,
establece que los valores de la función
se aproximan a un límite ,
conforme se aproxima a un número , sí el valor absoluto de la diferencia
entre
se puede hacer tan pequeña como se quiera tomando
suficientemente cercana a "b", pero no igual a "b".
3.2 Propiedades de los límites
Para resolver alguno limites es necesario tener en cuenta alguna de las
siguientes propiedades, a continuación iniciaremos con las más sencillas e irán
aumentando de dificultad, pero muchas veces teniendo en cuenta a anteriores
(1)
47
(2)
(donde c es una constante o numero cualquiera)
(3)
(e igual cuando es resta)
(4)
(5)
mientras que
En este ejemplo vamos a usar propiedades de los limites y algunos trucos para
romper la indeterminación de un límite, teniendo en cuenta que solo puedo
multiplicar y dividir por 1, usar la factorización o alguno otro procedimiento
matemático que no afecte al límite.
3.3 Límites laterales
Definición de límites laterales o unilaterales
Definición de límite por la derecha
Se dice que
si y solo si para cada
entonces
existe
es el límite por la derecha de
Observe que no hay barras de valor absoluto alrededor de
mayor que cero ya que
48
.
tal que si
en "a".
, pues
es
Definición de límite por la izquierda
Se dice que
entonces
Note que la expresión
si y solo si para cada
existe
tal que si
es el límite por la izquierda de
es mayor que cero, pues
en "a".
por lo que
.
En adelante determinaremos los límites laterales a partir de la representación
gráfica de una función cuya ecuación se da.
Ejemplo:
Determinar los límites, en los puntos de discontinuidad, de la función
por:
definida
Primero hagamos la gráfica de la función:
El punto de discontinuidad se presenta cuando
Luego:
y
Observe que el límite por la derecha (3), es diferente al límite por la izquierda
(2).
Ejercicio:
49
Represente la función definida por
y determine los límites laterales en el punto de discontinuidad.
Es posible demostrar que para que exista
los límites laterales existan y sean iguales.
Es decir,
si y solo si
Por consiguiente, si
existe.
es necesario y suficiente que
y
es diferente de
se dice que
Ejemplo:
Representemos gráficamente la función definida por:
Como
y
, entonces
Como
y
, entonces
no existe.
Ejercicio:
Considere la representación gráfica de la función definida por:
50
no
3.4 Asíntotas (verticales, horizontales u oblicuas)
Las asíntotas son rectas a las cuales la función se va aproximando
indefinidamente, cuando por lo menos una de las variables (x o y) tienden al
infinito.
Una definición más formal es:
Si un punto (x,y) se desplaza continuamente por una función y=f(x) de tal forma
que, por lo menos, una de sus coordenadas tienda al infinito, mientras que la
distancia entre ese punto y una recta determinada tiende a cero, esta recta
recibe el nombre de asíntota de la función.
Las asíntotas se clasifican en:
Asíntotas verticales (paralelas al eje OY)
Si existe un número “a” tal, que :
La recta “x = a” es la asíntota vertical.
Ejemplo:
es la asíntota vertical.
51
Asíntotas horizontales (paralelas al eje OX)
Si existe el límite: :
La recta “y = b” es la asíntota horizontal.
Ejemplo:
es la asíntota horizontal.
52
Asíntotas oblicuas (inclinadas)
Si existen los límites: :
La recta “y = mx+n” es la asíntota oblicua.
Ejemplo:
es la asíntota oblicua.
Las asíntotas horizontales y oblicuas son excluyentes, es decir la existencia de
unas, implica la no existencia de las otras.
En el cálculo de los límites se entiende la posibilidad de calcular los límites
laterales (derecho, izquierdo), pudiendo dar lugar a la existencia de asíntotas
por la derecha y por la izquierda diferentes o solo una de las dos.
Posición relativa de la función con respecto a la asíntota
Para estudiar la posición relativa de la función con respecto a la asíntota,
primero calcularemos los puntos de corte de ambas resolviendo el sistema:
53
Estos puntos determinan los cambios de posición de la función respecto de la
asíntota. Estos cambios quedarán perfectamente establecidos estudiando el
SIGNO [f(x)-Asíntota].
Ejemplo:
La función tiene por asíntota oblicua la recta
Calculamos los puntos de intersección de ambas:
El punto de corte de las dos funciones es P(2/3, 8/3).
Ahora estudiamos el signo de FUNCIÓN-ASÍNTOTA.
Esto nos indica que en el intervalo la función está por encima de la asíntota y
en el intervalo la función está por debajo de la asíntota.
3.5 Definición de continuidad
Definición de continuidad
54
Se dice que una función f es continua en c si y solo si se cumplen las tres
condiciones siguientes:
1.
está definida, (o sea, c pertenece al dominio de f)
2.
existe
3.
La función f será discontinua en c si por lo menos una de las condiciones
anteriores no se cumple.
Ejemplo
Determinar si la función
Primero
definida por
por
lo
es continua en
que
f
está
definida
en
2
Calculemos
(de aquí
Como
entonces f es continua en
Note que f no está definida ni en
esos puntos.
Ejemplo
Determine si la función definida por
es o no continua en
55
existe)
, ni en
por lo que f es discontinua en
Se tiene que
(es decir, 4 pertenece al dominio de )
Además
Pero
por lo que es discontinua en
.
La representación gráfica de la función es la siguiente:
3.6 Propiedades de la continuidad
Propiedades de continuidad
Si b es un número real y f, g son continuas en x = c, entonces:
1) bf es continua en c
(múltiplo escalar)
2) f ± g es continua en x = c
( suma o diferencia)
3) fg es continua en x = c
( producto)
4)
f
es continua en x = c
g
si g(c) ≠ 0 ( cociente)
Teorema-Función compuesta
Si g es continua en c y f es continua en g(c) , entonces ( f o g )(x) =
f(g(x)) es continua en x = c.
56
CAPÍTULO IV:
LA DERIVADA.
4.1 Definición de la derivada.
La derivada es uno de los conceptos más importante en matemáticas. La
derivada es el resultado de un límite y representa la pendiente de la recta
tangente a la gráfica de la función en un punto. Pero vayamos por partes.
La definición de derivada es la siguiente:
4.2 Interpretación geométrica y física de la derivada.
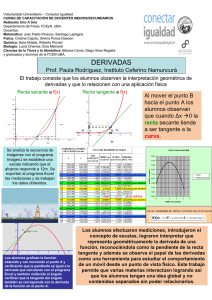
Cu a n do h t ien d e a 0 , e l pu n to Q t ie n de a co nf u nd irse co n e l P.
E n t on ce s la re ct a se ca n t e t ien d e a se r la re ct a t a n ge n t e a la
f u n c ión f (x) e n P , y p o r t a n t o e l ánαgulo
t ien d e a se r β.
57
L a pe n d ie n te d e la t a n ge n te a la cu rva e n u n p u nt o e s igu a l
a la de riva d a d e la f u n ción en e se pun t o .
m t = f '(a )
Da d a la pa rá b o la f (x) = x 2 , h a lla r lo s p un t o s e n lo s qu e la
re c t a t an ge n t e es p a ra le la a la b ise ct riz d e l p rim e r
c u a d ran t e .
L a b ise ct riz d e l p rim e r cu a d ran t e t iene com o e cua ció n y = x,
p o r t an t o su pe nd ie n t e e s m = 1 .
Co m o la s d o s re ct a s
p e nd ie n te , a sí qu e:
son
pa ra lela s
t e nd rá n
la
m isma
f'(a) = 1.
P o rqu e la p en d ient e d e la ta n ge nt e a la cu rva e s igu a l a la
d e riva d a e n e l pu nt o x = a .
58
4.3 Derivada de la función constante, derivada del producto de una
constante por una función, derivada de la función xn cuando n es un
entero positivo, y cuando n es un número real, derivada de una
suma de funciones, derivada de un producto de funciones y
derivada de un cociente de funciones.
Derivada de una función constante
Sea una función constante f(x) = C.
Su gráfica es, como se sabe, una recta paralela al eje de abscisas. Puesto que
para cualquier valor de la abscisa su ordenada correspondiente es,
constantemente, igual a C, si a es un punto cualquiera del campo de definición
de f(x), f(a + h) - f(a) = C - C = 0, por lo que
Luego la derivada de una constante es siempre cero.
59
Derivada de la función xn
Una función de carácter exponencial, cuyo exponente es un entero se
representa por f(x) = xn y se puede demostrar que su derivada es f'(x) = nxn − 1
por ejemplo tomemos la función:
f(x) = x3
Lo primero que se debe hacer es "bajar" el exponente de tal forma que éste
multiplique a la variable con respecto a cual estamos derivando, luego al mismo
exponente se le resta la unidad formando uno nuevo, así:
f'(x) = 3x3 − 1
Quedando finalmente:
f'(x) = 3x2
En algunas funciones donde la variable ya está siendo multiplicada, como: f(x)
= 7x4 se aplica la siguiente regla.
Derivada de una constante por una función
Cuando una función esté representada por medio de f(x) = cxn, su derivada
equivale a f'(x) = n(cx(n − 1)) de la siguiente manera:
Consideremos la siguiente función: f(x) = 8x4, lo primero a hacer es "bajar" al
exponente a multiplicar por la variable y el coeficiente que la acompaña, y de
nuevo se halla un nuevo exponente de la misma manera explicada
anteriormente:
f'(x) = 4(8x4 − 1)
Para obtener
f'(x) = 32x3
Cuando una constante acompaña a una variable cuyo exponente es 1 su
derivada será el valor de la constante:
f(x) = 7x
Entonces su derivada con respecto a esta variable será:
f'(x) = 7
Puesto que x0 = 1
60
Derivada de una suma
Se puede demostrar a partir de la definición de derivada, que la derivada de
una suma es la suma de la derivada de cada término por aparte. Es decir, (f +
g)' = f' + g'. Como ejemplo consideremos la función f(x) = 3x5 + x3, para
determinar su derivada se trabaja la derivada de cada termino por aparte y la
expresión de estos será la derivada de la función suma:
f'(x) = 15x4 + 3x2
Derivada de un producto
La derivada se expresa literalmente de la siguiente forma:
"La derivada de un producto de dos funciones es equivalente a suma entre el
producto de la primera función sin derivar y la derivada de la segunda función y
el producto de la derivada de la primera función por la segunda función"
Y matemáticamente expresado por la relación
Consideremos la siguiente función como ejemplo:
.
h(x) = (4x + 2)(3x7 + 2)
Identificamos a f(x) = (4x + 2) y g(x) = (3x7 + 2), utilizando las reglas
anteriormente expuestas, vemos que:
f'(x) = 4 y que g'(x) = 21x6
Por lo tanto
Simplificando y organizando el producto obtenido nos queda
h'(x) = 84x7 + 12x7 + 42x6 + 8
Sumamos términos semejantes y finalmente obtenemos la derivada:
h'(x) = 96x7 + 42x6 + 8
Derivada de un cociente
La derivada de un cociente se determina por la siguiente relación:
Es decir:
61
"La derivada de un cociente de dos funciones es la función ubicada en el
denominador por la derivada del numerador menos la derivada de la función en
el denominador por la función del numerador sin derivar, todo sobre la función
del denominador al cuadrado"
Este caso se relaciona mucho con la regla de derivada de un producto, pero
hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando
lo dicho anteriormente consideremos como ejemplo la siguiente función:
Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el
denominador que en este caso es g(x) = 2x y se multiplique por la derivada del
numerador que sería f'(x) = 3; luego la segunda parte dice que tomemos la
función del numerador (f(x)) sin derivar y lo multipliquemos por la derivada de
g(x) = 2x, que sería g'(x) = 2, todo esto lo dividimos entre el denominador al
cuadrado, así:
Ahora todo es cuestión de simplificar:
4.4 Derivada de las funciones exponenciales.
30
25
La función f(x) = ex
es una función
exponencial natural. Como 2<e<3, la
gráfica de f(x) = ex está entre f(x) = 2x y f(x)
= 3x, como se ilustra a la izquierda.
20
15
10
5
0
-5
0
5
Como e > 1, la función f(x) = ex es una función creciente. El dominio es el
conjunto de los números reales y el recorrido es el conjunto de los números
reales positivos.
Las calculadoras científicas contienen una tecla para la función f(x) = ex.
Geométricamente la pendiente de la gráfica de f(x) = ex en cualquier punto
(x,ex) es igual a la coordenada y de ese punto. Por ejemplo, en la gráfica de
f(x) = ex en el punto (0,1) la pendiente es 1.
62
Reglas para la derivación de funciones exponenciales:
Halla la derivada de:
1) y = e 2x - 1
3) y = x3ex
Ejercicios: Deriva cada una de las siguientes funciones:
1)
f(x) = e2x
2) y = e −2 x + x
3)
4)
5)
6)
7)
8)
9)
2
y=e x
g(x) = (e –x + e x)3
y = x2 e-x
y = x2 ex – 2x ex + 2 ex
f(x) = 4x
g(x) = 5 x – 2
h(x) = 2e x + 1
4.5 Derivada de las funciones trigonométricas.
Derivada de la función seno
A partir de la definición de la derivada de una función f(x):
63
Por tanto si f(x) = sen(x)
A partir de la identidad trigonométrica sin(A + B) = (sin(A)cos(B) + cos(A)sin(B),
se puede escribir
Agrupando los términos cos(x) y sin(x), la derivada pasa a ser
Reordenando los términos y el límite se obtiene
Ahora, como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del
límite para obtener
El valor de los límites
Son 1 y 0 respectivamente por Teorema del sándwich. Por tanto, si f(x) = sin(x),
Derivada de la función coseno
Si f(x) = cos(x)
A partir de la identidad trigonométrica cos(A + B) = cos(A)cos(B) − sin(A)sin(B),
se puede escribir
64
Operando se obtiene
Como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para
obtener
El valor de los límites
Son 1 y 0 respectivamente. Por tanto, si f(x) = cos(x),
Derivada de la función tangente
A partir de la regla del cociente, según la cual si la función que se quiere
derivar, f(x), se puede escribir como
y h(x) ≠ 0, entonces la regla dice que la derivada de g(x) / h(x) es igual a:
A partir de la identidad trigonométrica
haciendo
g(x) = sin(x) g'(x) = cos(x)
h(x) = cos(x) h'(x) = − sin(x)
65
sustituyendo resulta
operando
y aplicando las identidades trigonométricas
cos2(x) + sin2(x) = 1
resulta
f'(x) = sec2(x)
4.6 Derivada de las funciones compuestas (regla de la cadena).
En cálculo, la regla de la cadena es una fórmula para la derivada de la
composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de
derivadas cuando existe composición de funciones. Descripción de la regla: En
términos intuitivos, si una variable y, depende de una segunda variable u, que a
la vez depende de una tercera variable x; entonces, la razón de cambio de y
con respecto a x puede ser computado como el producto de la razón de cambio
de y con respecto a u multiplicado por la razón de cambio de u con respecto a
x.
En términos algebraicos, la regla de la cadena (para funciones de una
variable) afirma que si es diferenciable en y es una función diferenciable en
, entonces la función compuesta
en y
es diferenciable
Alternativamente, en la notación de Leibniz, la regla de la cadena puede
expresarse como:
66
Donde
indica que g depende de f como si ésta fuera una variable.
Ejemplos de aplicación
Supóngase que se está escalando una montaña a una razón de 0,5 kilómetros
por hora. La razón a la cual la temperatura decrece es 6 °F por kilómetro (la
temperatura es menor a elevaciones mayores). Al multiplicar 6 °F por kilómetro
y 0,5 kilómetros por hora, se obtiene 3 °F por hora, es decir, la razón de cambio
de temperatura con respecto al tiempo transcurrido.
Este cálculo es una aplicación típica de la regla de la cadena.
Por ejemplo si y = f(u) es una función derivable de u y si además u = g(x) es
una función derivable de x entonces y = f(g(x)) es una función derivable con:
o también
Ejemplo
y queremos calcular:
Por un lado tenemos:
y
si:
67
Entonces:
Si definimos como función de función:
Resulta que:
Con el mismo resultado.
Ejemplo
Tenemos
la cual se puede definir como
función compuesta. Si desglosamos la función compuesta quedaría:
,
cuyas
serían:
Con la regla de la cadena, esto sería:
Los cuales corresponden a las derivadas anteriormente extraídas.
68
derivadas
Se reemplazan las letras b y c pos sus valores NO derivados, no confundir.
Y luego se obtiene la derivada.
Derivadas de orden superior
Las fórmulas de Faà di Bruno generalizan la regla de la cadena a derivadas de
orden superior. algunas de ellas son:
4.7 Derivada de la función inversa.
Previo al estudio de las funciones trigonométricas inversas, es necesario
determinar la derivada de la función inversa de una función dada. Para ello
consideremos el siguiente teorema.
Teorema
Sea una función estrictamente creciente y continua en un intervalo
función inversa de .
69
la
Si
existe y es diferente de cero para
, entonces la función derivada
también existe y no es nula en el correspondiente "y" donde
Además se tiene que
.
Note que si
,y
entonces
.
Ejemplos:
1. Consideremos la función definida por:
Esta función posee función inversa definida por:
Se tiene que
Como
Note que:
2. Sea
la ecuación de una función definida en
.
Se tiene que
Así:
70
entonces
tal que
El teorema anterior será de gran utilidad cuando determinemos las derivadas
de las funciones trigonométricas inversas.
4.8 Derivada de las funciones logarítmicas
Vamos a estudiar la derivada de la función
definida por
, donde
tal que
Teorema
, entonces la función
Si
es
derivable sobre su dominio
Ejemplos:
1.
2.
Teorema
Sea
conjunto
, si la función
, entonces la función
derivable sobre
es derivable y
definida por
y
Ejemplos:
1.
2.
3.
( x 2 + 3) ⋅1 − ( x + 1)( 2 x )
1
=
log 5 e ⋅
2
x +1
( x 2 + 3)
2
x +3
71
sobre un
, es
.
En particular si la base de los logaritmos es " " entonces el
, y:
1.
2. Si
Ejemplos:
1.
2.
3.
4.
5.
6.
72
se denota por
, es decir
es
una
función
derivable
con
entonces:
4.9 Derivada de las funciones trigonométricas inversas.
Conviene recordar que:
a. Si una función es continua y estrictamente creciente (decreciente) en un
intervalo, entonces posee función inversa la cual también es continua y
estrictamente creciente (decreciente).
b. Las funciones trigonométricas son periódicas por lo que la correspondencia
entre la variable independiente y la dependiente no es "uno a uno".
De aquí se tiene que la inversa de una función trigonométrica no es una
función,
es
una
relación.
Sin embargo, si se restringe el dominio de una función trigonométrica se
establece una relación biunívoca y la inversa de la función trigonométrica sí es
una función.
Función seno inverso
Al considerar la gráfica de la función seno:
Se observa que en varios intervalos, por ejemplo:
, etc, la función seno es continua y estrictamente
creciente, por lo que podría escogerse alguno de ellos para definir la función
inversa de la función seno. Usualmente se toma el intervalo
define la función seno como:
La función
. Luego, se
así definida es continua y estrictamente creciente en el intervalo
, por lo que existe una única función, definida en el intervalo
,
llamada función seno inverso. Esta función, denotada arcsen, se define como
sigue:
73
Se tiene entonces que
Luego,
.
es el único número
para el cual
.
Ejemplos:
a.
b.
c.
d.
La representación gráfica de la función seno y de la función arcoseno es la
siguiente:
Derivada de la función seno inverso
Como
de la derivada de una función inversa se tiene que:
74
, aplicando el teorema
Como
,
pues
y
entonces
.
Luego:
En general
Ejemplos:
1.
2.
3.
Ejercicio:
Determine
si:
a.
b.
Función coseno inverso
Como en la función seno, la función coseno es continua y estrictamente
decreciente en varios intervalos, por lo cual debe restringirse su dominio de tal
forma que posea función inversa.
Sea entonces la función
La función
tal que:
así definida es continua y estrictamente decreciente en el intervalo
, por lo que posee función inversa. Esta recibe el nombre de arco coseno,
(o función coseno inverso), y se denota
.
Se define de la siguiente forma:
75
Se tiene que
Luego,
es el único número
con
para el que
Ejemplos:
a.
b.
c.
d.
La representación gráfica de la función coseno y la de la función arco coseno
es la siguiente:
Derivada de la función coseno inverso
Como
derivada de la función inversa se tiene que:
76
, aplicando el teorema de la
Como
,
pues
y
entonces
.
Luego:
En general
Ejemplos:
1.
2.
3.
Ejercicio:
Determine
si:
a.
b.
Función tangente inversa
Igual que en los dos casos anteriores, vamos a restringir el dominio de la
función tangente al intervalo
, en el que es continua y estrictamente
creciente, por lo que posee función inversa.
Luego se define la función tangente como:
Se define la función tangente inversa, también llamada arco tangente, y
denotada
, como:
77
Se tiene que
Luego,
,
es el único número
con
para el que
Ejemplos:
a.
b.
c.
Además:
La representación gráfica de la función tangente y la de la función arcotangente
es la siguiente:
78
Derivada de la función arcotangente
Como
derivada de la función inversa se tiene que:
Como
,
y
entonces
, aplicando el teorema de la
por
lo
que:
En general
Ejemplos:
1.
2.
3.
Ejercicio:
Determine
si:
a.
b.
c.
4.10 Derivada de las funciones implícitas.
Al considerar la función con ecuación
, es posible determinar
con los teoremas enunciados anteriormente, ya que es una función dada
implícitamente en términos de la variable independiente .
79
Sin embargo, existen funciones que no están definidas en forma explícita,
ejemplos de las cuales son las siguientes:
Estas ecuaciones no pueden ser resueltas explícitamente para "y" en términos
de "x". Se dice que la función f está definida implícitamente por las
ecuaciones:
respectivamente.
Note que ambas expresiones son de la forma general
.
Interesa ahora determinar la derivada de una función dada en forma implícita.
Consideremos cada una de las ecuaciones anteriores:
a.
Observe que
involucra un producto de funciones y que para derivar
se debe utilizar la regla de la cadena.
Se tiene entonces derivando:
Despejando
se tiene que:
Sustituyendo "y" por
80
se obtiene:
b.
derivando
de donde
y sustituyendo
se tiene:
El proceso realizado en estos dos ejemplos recibe el nombre de derivación
implícita, y puede ser utilizado únicamente bajo el supuesto de que la ecuación
dada especifica una función. En caso de que no sea así, aunque se realicen las
operaciones, el resultado carece de sentido.
Ejemplos:
1. Suponiendo que existe una función derivable
implícitamente por la ecuación
tal que
está definida
, calcular
Solución:
Derivando implícitamente se obtiene:
Note que hemos trabajado como si
.
2. En cada caso determinar una ecuación para la recta tangente y una
ecuación para la recta normal a la gráfica de la ecuación dada en el
punto . Graficar la curva, la recta tangente y la recta normal.
81
a.
b.
Solución:
a.
Primero obtenemos
que nos da la pendiente de la recta tangente:
de donde
Evaluando
Luego
se tiene que
. Sustituyendo
se obtiene que
por lo que la
ecuación de la recta tangente es
La pendiente de la recta normal es
recta es:
de donde la ecuación de esta
; sustituyendo nuevamente en
se obtiene que
La ecuación de la recta normal es:
La
ecuación
puede
escribirse
como
que representa la ecuación de una circunferencia
con centro en
y radio .
La representación gráfica de la curva y las rectas es la siguiente:
82
b.
Dada la ecuación
Evaluando en
obtenemos
. como
entonces
se tiene que
Luego, la pendiente de la recta tangente es
. Sustituyendo
y la ecuación es
en esta ecuación se obtiene que
que finalmente la ecuación de la recta tangente es
La pendiente de la recta normal es
. Sustituyendo
.
y la respectiva ecuación es:
se obtiene que
ecuación de la recta normal es
por lo
por lo que la
.
La representación gráfica de la curva, las recta tangente y de la recta
normal es la siguiente:
4.11 Derivadas sucesivas.
Si es una función diferenciable, es posible considerar su función derivada
como:
para en el dominio
Si para algunos valores
de .
existe el
segunda derivada de la función que se denota por
83
se dice que existe la
o
, que equivale
a
. O sea, la segunda derivada de la función se obtiene derivando la
primera derivada de la función.
Ejemplos:
1. Si
entonces:
y
2. Si
entonces:
y derivando nuevamente
Por tanto
Similarmente podemos decir que la derivada de
tercera derivada de respecto a "x" que se denota
respecto a "x" es la
o
La derivada de la tercera derivada es la cuarta derivada
continuar sucesivamente hasta la enésima derivada de
.
y así podríamos
que se denota por
o
. Generalmente se habla del orden de la derivada; así la primera
derivada es la derivada de primer orden, la segunda es la de segundo orden, la
enésima derivada es la derivada de orden n.
Ejemplos:
1. Determinar
Solución:
84
, donde
Obtenemos primero
Luego:
y se tiene que:
2. Determinar
Solución:
Se tiene que:
2 −32 8 −53
f ´( x) = x − x + 1
3
5
=
f ´( x)
−4 −35 24 −58
x + x
9
25
Por último:
f=
´´´( x)
20 −38 192 −513
x −
x
27
125
Una aplicación de la segunda derivada
Anteriormente hemos estudiado que si
partícula al origen en un tiempo , entonces
nos indica la distancia de una
es la velocidad en el tiempo
Al calcular la derivada de la velocidad respecto al tiempo, es decir, al calcular
se obtiene la aceleración instantánea en el tiempo . Si denotamos esta
aceleración por
se tiene que
, es decir, la aceleración es la
segunda derivada de la distancia respecto al tiempo.
85
Ejemplo:
Sea
, la ecuación que determina la distancia en el tiempo (en
segundos) de una partícula al origen en un movimiento rectilíneo. Determinar el
tiempo, la distancia, y la velocidad en cada instante en que la aceleración es
nula.
Solución:
Si
entonces la velocidad, está dada por:
Averigüemos el tiempo en que la aceleración se hace cero.
Luego, la distancia recorrida cuando
es
es
metros y la velocidad en
.
4.12 Teorema del valor medio y teorema de Rolle.
Teorema del valor medio para derivadas (Teorema de Lagrange)
Sea una función que cumple las propiedades siguientes:
1. Es continua sobre un intervalo cerrado
2. Es derivable sobre un intervalo abierto
Entonces existe por lo menos un número
tal que
y
Este teorema se utiliza para demostrar varios teoremas tanto del cálculo
diferencial como del cálculo integral.
Interpretación geométrica
El teorema del valor medio puede interpretarse geométricamente como sigue:
Consideremos la representación gráfica de una curva continua :
86
La recta secante que une los puntos
tiene como pendiente
. Según el teorema del valor medio, debe existir algún punto
sobre la curva, localizado entre P y Q, en el que la recta tangente sea paralela
a la recta secante que pasa por P y Q; es decir, existe algún número
tal
que
Ejemplos:
Para cada función cuya ecuación se da, verificar que se cumplen las
condiciones del teorema del valor medio en el intervalo dado, y determinar un
valor adecuado "c" que satisfaga la conclusión de este teorema:
1.
2.
Solución:
1. Por ser
una función polinomial, es derivable para toda
debe existir por lo menos un número
Además
Como
87
tal que:
por lo que
entonces
por lo que
por lo que
Luego en
y en
la recta tangente
es paralela a la recta secante que pasa por los puntos
2. Como
es continua en el intervalo
y
.
y derivable en el intervalo
cumplirá ambas condiciones en el intervalo
Luego debe existir por lo menos un número
tal que
,
Como
entonces
por lo que
Resolviendo la ecuación se obtiene que
Aunque ambos valores de
o
pertenecen al intervalo
,se tiene que
únicamente cuando
Luego en
la recta tangente es paralela a la recta secante que
pasa por los puntos
Gráficamente se tiene:
88
.
Teorema de Rolle (o teorema sobre las
raíces de la derivada)
Sea una función que cumple las condiciones
siguientes:
1.
es continua sobre un intervalo cerrado
2.
es derivable sobre un intervalo abierto
3.
Entonces existe por lo menos un número real
tal que
O sea
.
para cierto
.
Interpretación geométrica
Este teorema puede interpretarse geométricamente de la manera siguiente:
Si una curva continua interseca al eje
en
y tiene una recta
tangente en cada uno de los puntos del intervalo
, entonces existe por lo
menos un punto de la curva en el que la recta tangente es paralela al eje .
Gráficamente se tiene:
El teorema también es válido para una función derivable que aunque en los
extremos del intervalo
"a" y "b", es decir,
89
no interseque al eje
.
, sí tome valores iguales para
Es necesario que la función posea derivada en todos los puntos del intervalo,
ya que aunque la función sea continua en el intervalo, si no es derivable en
algún punto, puede suceder que no exista ningún valor "c" para el que
igual a cero.
Por ejemplo, la función
con ecuación
y además se cumple que
está definida para
intervalo dado.
es continua en el intervalo
, pero la derivada de
, y se tiene que
La representación gráfica de esta función en el intervalo
Ejemplos:
90
sea
no
no se hace cero en el
es la siguiente:
Para cada una de las funciones cuyas ecuaciones se dan a continuación,
verificar que se cumplen las condiciones del teorema de Rolle en el intervalo
indicado, y determinar un valor adecuado "c" que satisfaga la conclusión de
este teorema:
1.
2.
Solución:
1. Por ser una función polinomial es derivable y por lo tanto continua para
todo
. se cumplen entonces las dos primeras condiciones en el
intervalo
por lo que la curva interseca al eje
Además
cumple la tercera condición.
Luego, debe existir por lo menos un número
si y solo si
Como
Luego en el punto
2. De nuevo,
tal que
entonces puede tomarse
la recta tangente es paralela al eje
es una función polinomial y por tanto es derivable, y
continua para toda
. En particular, en el intervalo
las dos primeras condiciones.
Además
91
y se
se cumplen
verificándose la tercera condición.
Luego, el teorema es válido en el intervalo
.
Como
entonces
y existe
si
tal que
y
solo
si
. Note que ambos valores pertenecen al intervalo
.
Luego, en los puntos
, la
recta tangente tiene pendiente cero y por tanto dicha recta es paralela al
eje .
92
CAPÍTULO V:
APLICACIONES DE
LA DERIVADA.
5.1 Recta tangente, normal e intersección de curvas.
Recta tangente
La recta tangente en un punto de una circunferencia es aquella recta que
intercepta a la circunferencia en un solo punto, pero lo cierto es que tal
definición no es suficiente para una curva en general porque en otros casos la
recta tangente puede llegar a interceptar a la curva en uno o más puntos,
además de ser inclinada, horizontal o vertical.
y = x3+1
y = sen x
Ejemplo 1
Ejemplo 2
Ejemplo 3
Para obtener una definición adecuada de la recta tangente a la gráfica de una
función en un punto se emplea el concepto de límite
Ecuación de la recta tangente
Sea f una función continua en xo. La ecuación de la recta tangente a la curva
en xo es:
Sea f una función continua en xo. La ecuación de la recta tangente a la curva
en xo es:
i) y = f '(xo) . x + b, si la función es derivable en x0.
93
ii) x=xo, si la derivada, cuando x tiende a xo por la izquierda y por la derecha, es
más infinito (o menos infinito).
1. Cálculo de la ecuación de la recta tangente a f(x)=x3+1 en xo=0.5.
Derivamos la función f '(x)=3x2.
Evaluamos la derivada en 0,5, f '(0.5)=mt=0.75.
Calculamos la ordenada de xo=0.5 que es yo=f(xo)=1.13.
Sustituimos los valores dados en la ecuación de la recta tangente a la
curva, es decir en yo=mt xo + b, para obtener b=0.75.
5. Escribimos la ecuación de la recta tangente: y = 0,75 x + 0,75
1.
2.
3.
4.
2. Cálculo de la ecuación de la recta tangente a y= sen x en xo=pi/2.
1.
2.
3.
4.
5.
Derivamos la función y' = cos x.
Evaluamos la derivada en pi/2 para obtener mt= 0
Calculamos la ordenada de xo=pi/2, que es yo=1.
Calculamos la ordenada en el origen de la recta tangente, b=1.
Escribimos la ecuación de la recta tangente: y=1
3. Cálculo de la ecuación de la recta tangente a la siguiente curva en el punto
de abscisa cero.
1. La derivada
2. Se observa que el dominio de la función es D=R, pero que la primera
derivada no está definida en cero.
3. Analizando la derivada cuando x tiende a 0 por la izquierda y derecha se
sabe que y' es más infinito en ambos casos, entonces la ecuación de la
recta tangente es vertical y su ecuación: x=0
4. Cálculo de la ecuación de la recta tangente a la circunferencia x2 + y2 = 5 en
xo= -2.
1. La derivada es y' = -(x/y) (Obtenerla derivando
implícitamente).
2. La ordenada para xo= - 2 es yo= -1.
3. La derivada evaluada en (-2,1) es mt= - 2.
4. La ordenada en el origen de la recta tangente b= - 5.
5. La ecuación de la recta tangente: y = - 2x- 5
94
la
función
5.2 Máximos y mínimos (criterio de la primera derivada).
Extremos Absolutos
Las palabras máximas y mínimas, pertenecen a un lenguaje habitual y
los usamos generalmente cuando deseamos expresar, lo más grande o lo más
pequeño de la cantidad comparada. Este es el mismo significado que toma en
el cálculo. “Para cada función es posible establecer comparaciones entre las
imágenes, en un intervalo dado, y de acuerdo a la medida conocer la mayor
imagen y desde luego, al menor. Estos serán llamados extremos de la función,
o de manera más específica, máximo absoluto y mínimo absoluto
respectivamente”.
Precisaremos aun más:
Definición:
Máximo y mínimo absolutos: Sea f una función continua definida en [a, b].
Sea c y d dos números del intervalo, tales que:
f (c) ≥ f (x) para todo x ∈ [a, b]
y
f (d) ≤ f (x) para todo x ∈ [a, b]
Llamamos a f(c) el máximo absoluto de f en [a, b] y a f(d) el mínimo absoluto
de f en [a, b]
Es conveniente hacer algunas reflexiones sobre la definición anterior.
Primeramente, es evidente en la Figura que:
Máximo absoluto = f (b)
y
Mínimo absoluto = f (a)
f (b)
f (a)
x
a
b
Sin embargo, ¿Cuál es el máximo absoluto y el mínimo absoluto en la función
constante que aparece en la Figura?
95
Con esto deseamos enfatizar lo siguiente: el máximo o el mínimo son números
que resultan de la comparación de los valores que toma la función en su
dominio. No representa la imagen de algún argumento en particular,
independientemente de que ésta los tome. Así, este número llamado máximo
(o mínimo) absoluto, puede corresponder al valor de la función para uno o más
argumentos del dominio.
Otro aspecto importante es el hecho de que los extremos absolutos
pueden o no coincidir con los límites del intervalo que da el dominio, como se
verá en el ejemplo 1:
Ejemplo 1.- Dada f (x) = x2 –2x, calcular los extremos absolutos en el
intervalo
[0, 3].
SOLUCIÓN:
Como
observa, su vértice
encuentra en x = 1, y
él se encuentra
mínimo absoluto.
y
0
3
Si x = 0
x
se
se
en
el
Resulta también
evidente que el máximo
absoluto corresponde a
la imagen en x = 3.
Si x = 2
f (x) = (0)2 –2 (0) = 0
f (x) = (2)2 –2 (2) = 4 – 4 =
0
Si x = 1
Si x = 3
F (x) = (1)2 –2 (1) = 1 – 2 = -1
f (x) = (3)2 –2 (3) = 9 – 6 = 3
∴ Máximo absoluto = 3
para x = 3
Mínimo absoluto = -1 para x = 1
Extremos Relativos
Definición:
Máximos y mínimos relativos: Sea f una función derivable en [a, b]. Sea c ∈
(a, b), tal que f'(c) = 0. Decimos que f(c) es un extremo relativo (o extremo
96
local), si es posible encontrar un subintervalo de [a, b] que contenga a c en
donde f (c) sea un extremo absoluto.
y
Por ejemplo, en la Figura 53,
f ‘ (c) = 0
los extremos absolutos son:
Máximo absoluto = f (b)
Mínimo absoluto = f (a)
f '(d) = 0
a
c
d
b
x
Figura
Sin embargo existen otros casos en donde si se restringe el dominio, los
números anteriores se comportan como extremos. Por ejemplo, la función de la
Figura 53 tiene un máximo en x = c, dentro del intervalo [a, d], y un mínimo en x
= d, dentro del intervalo [c, d]. Así, de acuerdo a la definición:
Máximo relativo = f (c)
Mínimo relativo = f (d)
Los extremos relativos podrán localizarse al resolver la ecuación f '(x) = 0, ya
que entre sus raíces se encuentran las abscisas de estas; sin embargo, no
todas las raíces corresponderán necesariamente a un extremo. Podría tratarse
también de un punto como el que se ilustra en la Figura.
y
En donde, a pesar
de que la derivada se
anula en x = c, no se puede
hallar en [a, b] ningún
f '(c) = 0
subintervalo en donde f(c)
sea, ya un máximo o un
mínimo.
x
a
97
c
b
“Llamaremos número crítico a cualquier argumento c del dominio de la función
f, tal que f '(c) = 0. Así, los máximos y mínimos locales tendrán siempre como
abscisa un número crítico. Por otra parte, si c es un número crítico para f,
entonces el punto (c, f(c)) será llamado punto crítico de f”.
Ejemplo 1.- Cuales son los números críticos de la función f (x) = x3 + 3x2 –9x +
3 y cuales son sus puntos críticos.
Números Críticos
f(x) = x3 + 3x2 –9x + 3
Puntos críticos
f'(x) = 3x2 + 6x –9
Si x = -3
f'(x) = 0
f(-3) = (-3)3+3(-3)2–9(-3)+3
3x2 + 6x –9 = 0
x2 + 2x – 3 = 0
=-27+27+27+3=30
(-
3, 30)
Si x = 1
f(1) = (1) + 3(1) –9(1) + 3 = 1 + 3 –9 +3 =-2
(1, -2)
Criterio de la Primera Derivada para Extremos Relativos
Sea f una función continua en un intervalo I; sean a, b, c puntos de I, tales que
a < c < b y c un punto crítico de f (f ’(c) = 0 o f ‘ ( c) no existe).
Entonces:
i.
Si
para todo x en (a, c) y
para todo x en (c, b),
entonces, f(c) es un máximo relativo. (fig. 9.13. (a), fig. 9.13. (b)).
ii.
Si
para todo x en (a, c) y
para todo x en (c, b),
entonces, f(c) es un mínimo relativo. (fig. 9.13. (d), fig. 9.13. (e)).
iii.
Si
para todo x en (a, c) y
para todo x en (c, b),
entonces, f(c) no es un extremo relativo. (fig. 9.13. (c)).
iv.
Si
para todo x en (a, c) y
Para todo x en (c, b), entonces, f(c) no es un extremo relativo.
98
5.3 Máximos y mínimos (criterio de la segunda derivada.)
Criterio de la segunda derivada para establecer los valores máximos y
los valores mínimos de una función
Además de proporcionar información sobre la concavidad de la gráfica de una
función, la segunda derivada permite establecer si un punto crítico es un valor
máximo o un valor mínimo.
El siguiente teorema se refiere a este segundo aspecto.
Teorema
Sea f una función con dominio D.
Si
está definida para
donde
y si
con
entonces:
a.
es un valor máximo relativo de f si se cumple
que
es un valor mínimo relativo de f si se cumple
b.
que
Ejemplos:
Utilizando el teorema anterior vamos a determinar los valores máximos y los
valores mínimos de las funciones cuyas ecuaciones son:
1.
,
Note que la función f no está definida en
La derivada de f está dada por
Los valores críticos de f se obtienen cuando
99
,
. En este caso,
si y
solo si
,ó
.
Ahora, la segunda derivada de f es
Vamos a evaluar
a.
b.
en
; como
relativo de f.
y en
entonces
; como
máximo relativo de f.
es un valor mínimo
entonces
es un valor
Gráficamente se tiene en el intervalo
5
3
2. g ( x) = ( x − 9)( x − 1) 3
8
Se tiene que
La primera derivada de g está dada por
2
g ′( x) =
( x − 6)( x − 1) 3
Como
cuando
y cuando
entonces estos son los valores
críticos de g.
La segunda derivada de g es
100
Evaluando
en
que es mayor que cero, por lo que
se tiene que
g ′′(6) = 3 35
es un valor mínimo relativo de g.
Observe que no puede evaluarse en
pues hace cero el denominador por
lo que para este valor crítico debe utilizarse el criterio de la primera derivada.
Analizando
se obtiene que
para
y
para
por lo que al no existir cambio de signo resulta que
máximo ni mínimo. El gráfico de g se muestra a continuación.
no es ni
5.4 Funciones crecientes y decrecientes.
Funciones crecientes y decrecientes y su relación con la derivada
Sea f una función continua con ecuación
, definida en un intervalo
La siguiente es la representación gráfica de f en el intervalo
.
En la representación gráfica anterior puede observarse que la función f es:
101
.
1. Creciente en los intervalos
,
2. Decreciente en los intervalos
,
También se tiene que cuando la pendiente de la recta tangente es positiva, la
función f crece; y cuando la pendiente de la recta tangente es negativa, la
función decrece.
,
y
la recta tangente
Note además que en los puntos
es horizontal, por lo que su pendiente es cero, es decir, la primera derivada de
la función se anula en cada uno de esos puntos.
En los siguientes teoremas se formalizan las apreciaciones anteriores.
Teorema 1
Sea f una función continua en un intervalo cerrado
el intervalo abierto
1. Si
2. Si
.
para toda x en
creciente en
, entonces la función f es
.
para toda x en
decreciente en
y derivable en
, entonces la función f es
.
Ejemplos:
1. Determinemos los intervalos en que crece o decrece la función con
ecuación
.
Para ello calculemos la primera derivada de
Como
.
, o sea si
, entonces f es creciente para
, o sea si
, entonces f es decreciente para
.
Como
.
102
En la representación gráfica de la función puede observarse lo obtenido
anteriormente.
2. Determine en cuáles intervalos crece o decrece la función con ecuación
con
.
que puede escribirse como
La derivada de f está dada por
Como
es positivo para toda x en
entonces:
y
Para resolver estas desigualdades recurrimos a la siguiente tabla.
103
Luego:
si
por lo que la función f crece en el
.
intervalo
Además:
si
intervalo
de donde la función f decrece en el
.
La representación gráfica de la función es la siguiente:
3.
5.5 Concavidades y puntos de inflexión.
Definición de concavidad
Se dice que la gráfica de una función f es cóncava hacia arriba en un
intervalo A,
, si
es creciente sobre A. Si
sobre A entonces se dice que la gráfica de f es cóncava
es decreciente
Note que es la función derivada la que debe ser creciente o decreciente en el
intervalo
A.
En la siguiente representación gráfica, una función f es cóncava hacia arriba en
el intervalo
104
y cóncava hacia abajo en el intervalo
Teorema
cuando
Si f es una función tal que
cóncava hacia arriba sobre
, entonces la gráfica de f es
.
Demostración:
Si
y como
, entonces se tiene que
es creciente sobre
por lo que de acuerdo con la definición de concavidad de una función, se
obtiene que f es cóncava hacia arriba sobre
.
Teorema
Si f es una función tal que
cóncava hacia abajo sobre
cuando
, entonces la gráfica de f es
.
Demostración:
De la hipótesis:
, y como
decreciente sobre
, se obtiene que
es
por lo que según la definición dada sobre concavidad, la
gráfica de la función f es cóncava hacia abajo sobre
.
Ejemplifiquemos los dos teoremas anteriores utilizando la función f con
ecuación
Si
105
entonces
, y,
Luego,
si
y,
Como
pues en ellos
pues en el
, entonces
si
.
es creciente en los intervalos
es positiva. Además
,
es decreciente en el intervalo
es negativa.
Luego, f es cóncava hacia arriba en el intervalo
abajo en el intervalo
y cóncava hacia
.
La representación gráfica de la función
es la siguiente:
Representación gráfica de la función
Observe que
es creciente en
y
y decreciente en
.
Representación gráfica de la función f:
Representación gráfica de la función f
Note que f es cóncava hacia arriba en los intervalos
hacia abajo en el intervalo
106
.
y cóncava
Damos ahora la definición de punto de inflexión
Definición
Se dice que
existe un intervalo
sobre
es un punto de inflexión de la gráfica de una función f, si
tal que
, y la gráfica de f es cóncava hacia arriba
, y cóncava hacia abajo sobre
, o viceversa.
Podemos representar lo anterior en forma gráfica como sigue:
Ejemplos:
1.
El punto
es un punto de inflexión de la curva con ecuación
, pues
es positiva si
donde f es cóncava hacia arriba para
.
Gráficamente se tiene:
107
, y negativa si
, de
, y cóncava hacia abajo para
2.
Determinemos los puntos de inflexión de la función f con ecuación
Se tiene que
por lo que
Resolvamos las desigualdades
Como
si
hacia arriba en esos intervalos.
entonces la gráfica de f es cóncava
La gráfica de f es cóncava hacia abajo en el intervalo
pues en él
.
Luego los puntos
y
son puntos en los que cambia la
concavidad y por tanto son puntos de inflexión.
108
La gráfica de la función f es la siguiente:
Puede decirse que un punto de inflexión separa una parte de la curva
que es cóncava hacia arriba de otra sección de la misma que es
cóncava hacia abajo.
En un punto de inflexión, la tangente a la curva recibe el nombre de
tangente de inflexión. Gráficamente:
Observe que una parte de la curva queda sobre la tangente de inflexión,
y otra parte bajo ella.
109
5.6 Estudio general de curvas.
Trazo de curvas
La teoría estudiada hasta ahora sobre máximos y mínimos de una función, será
aplicada tanto en la resolución de problemas como en el trazo de la gráfica de
una curva. Para este último aspecto nos hace falta estudiar las asíntotas de
una curva, tema que veremos a continuación para pasar luego al trazo de
curvas
y
por
último
a
la
resolución
de
problemas.
Asíntotas
es necesario estudiar la variación de la
Dada una curva con ecuación
función cuando la abscisa y la ordenada de un punto cualquiera de la curva
tiende al infinito.
Definición
Cuando el punto
de una curva se desplaza a lo largo de ella, de tal forma
que su distancia al origen tienda a infinito, puede suceder que la distancia de
P a una recta fija, tienda a cero. Esta recta recibe el nombre de asíntota de la
curva.
Gráficamente:
Asíntota horizontal:
Sea la función con ecuación
Si
ó
, entonces la recta con ecuación
asíntota horizontal de la gráfica de f.
Ejemplo: Sea
110
la ecuación de una curva.
es una
Como:
entonces la recta con ecuación
Entonces la recta con ecuación
Gráficamente se tiene:
es una asíntota horizontal de la curva.
es una asíntota horizontal de la curva.
Asíntota vertical:
La recta con ecuación
con ecuación
es una asíntota vertical de la gráfica de una función
, si se cumple alguna de las siguientes condiciones.
i.
iii.
ii.
iv.
es una asíntota vertical de la gráfica de una
Si la recta con ecuación
función f, entonces f es discontinua en "a".
Ejemplo:
Sea
111
la ecuación de una curva.
Observe que el dominio es el conjunto:
Como
y
entonces la recta con ecuación
curva.
es una asíntota vertical de la gráfica de la
Gráficamente:
Note que la recta con ecuación
, (eje x), es asíntota horizontal de la curva.
Asíntota oblicua
Especificaremos ahora los pasos a seguir para hacer el análisis y la gráfica de
una función f cuya ecuación se da.
1. Calcular el dominio de f.
2. Averiguar las intersecciones con los ejes coordenados.
Si
es la ecuación de la curva, los puntos de intersección con el
eje x se determinan resolviendo la ecuación
, los puntos de
intersección con el eje Y se calculan dándole a x el valor cero.
3. Sentido de variación
Se hace el estudio de la primera derivada.
a.
b.
Se calcula
Para determinar los valores críticos se resuelve
c. Para determinar los intervalos en que f crece y en los que
112
decrece se resuelven las desigualdades
, y,
4. Estudio de la segunda derivada de f.
a.
Se calcula
b.
Se determinan los puntos de inflexión resolviendo
c. Para determinar los intervalos en que f es cóncava hacia arriba y en
los que es cóncava hacia abajo, se resuelven las desigualdades
y
Los puntos máximos y los puntos mínimos se pueden establecer ya sea
utilizando el criterio de la primera derivada o el de la segunda derivada.
5.7 Derivada como razón de cambio y aplicaciones.
Puede interpretarse el concepto de la velocidad en el movimiento rectilíneo,
estudiada en la sección 4.2, como el concepto más general de la razón de
cambio instantáneo. Es esta una razón de cambio de la distancia respecto al
tiempo, y si s = f (t ) describe un movimiento rectilíneo, está razón de cambio
en cualquier instante t, está representada por f ′ ( t0 ) . De modo semejante a
menudo nos interesamos en una razón de cambio de una cantidad respecto a
otra. Existen muchas aplicaciones del concepto de razón instantáneo y razón
promedio tanto en Ingeniería, Economía, Física, Química, así como también en
Matemáticas. Son ejemplos, la razón de cambio del área de un círculo respecto
a su diámetro, la razón de cambio de la longitud de una varilla de metal
respecto a su temperatura, la razón de la solución de un compuesto químico en
un solvente respecto al tiempo así como por ejemplo, la cantidad de agua Q(lts)
que hay en un recipiente es función del tiempo t. Si el agua entra y sale, Q
cambia en una cantidad ∆Q de un tiempo t a un tiempo t + ∆t . Entonces la
razón de cambio media o promedio de Q con respecto a t es:
dQ
∆Q
∆Q
= lim
( lt / min ) y la razón instantánea:
(1t / min )
∆t
dt ∆t →0 ∆t
Es decir, con frecuencia tales problemas pueden analizarse de una manera
completamente igual a la empleada para los problemas de la tangente y de la
velocidad. Así, si se da y en términos de x por una fórmula y = f ( x) podemos
discutir la razón de cambio de y respecto a x.
113
Por razón de cambio de media de y respecto a x, desde x = x0 hasta x = x , se
entiende la relación:
f ( x) − f ( x0 ) cambio de ordenadas
=
x − x0
cambio de abscisas
Si el cociente diferencial tiene un límite cuando x → x0 , este límite está acorde
con nuestro concepto intuitivo de razón de cambio instantáneo de y con
respecto a x.
Definición: La razón de cambio instantáneo de f ( x) respecto a x en x1 es la
derivada f ′ ( x1 ) siempre que la derivada exista.
Ejemplos:
1).
Hallar la razón de cambio del área de un cuadrado respecto a un lado
cuando el lado mide 5 pulgadas.
Solución:
Sea
=
A f=
(a ) a 2 , el área del cuadrado como función de su lado. Entonces:
2
′(a ) D=
=
Da A f=
2a
a a
pu lg 2 / pu lg
a = 5 pu lg
⇒
10 pu lg 2 / pu lg.
Da A =
Todas las cantidades que se encuentran en la vida diaria cambian con el
tiempo. Esto es cierto especialmente en las investigaciones científicas. Por
ejemplo, un químico puede estar interesado en la cantidad de cierta substancia
que se disuelve en el agua por unidad de tiempo. Un ingeniero eléctrico puede
querer saber qué tanto cambia la corriente en alguna parte de un circuito
eléctrico por unidad de tiempo. Un biólogo puede estudiar el aumento (o la
disminución), por unidad de tiempo, del número de bacterias de algún cultivo.
Pueden citarse muchos otros ejemplos, incluyendo algunos en campos fuera
de las ciencias naturales. Consideremos la siguiente situación que puede
aplicarse a cualquiera de los ejemplos anteriores.
Supongamos que una variable w es función del tiempo de manera que al
tiempo t , w está dada por w = g ( t ) , donde g es una función derivable. La
diferencia entre el valor inicial y el valor final de w en el intervalo de tiempo
[t , t + h] está dada por g ( t + h ) − g (t ) . Análogamente a lo que hicimos
tratamiento del concepto de velocidad, formulamos la siguiente definición.
114
DEFINICIÒN
La razón media de cambio de w = g (t ) en el intervalo [t , t + h ] es
g (t + h) − g (t )
h
La razón de cambio de w = g (t ) con respecto a t es
dw
g (t + h) − g (t )
′(t ) lim
= g=
h →0
dt
h
Las unidades que deben usarse en al definición dependen de la naturaleza de
la cantidad representada por w . A veces dw / dt se llama la razón de cambio
instantáneo de w con respecto a t .
El límite de este cociente cuando h tiende a 0 (es decir, dy / dx ) se llama la
razón de cambio de y con respecto a x. Así, si la variable x cambia, entonces
y cambia a razón de dy / dx unidades por unidad de cambio de x. Por ejemplo,
supongamos que cierta cantidad de gas está encerrada en un globo. Si el gas
se calienta o se enfría mientras la presión permanece constante, el globo se
dilata o se contrae y su volumen V es una función de la temperatura t. La
derivada dV / dT nos da la razón de cambio del volumen con respecto a la
temperatura.
5.8 Regla de L`Hôpital.
Teorema: Regla de L'Hôpital
Sean
funciones que satisfacen las condiciones del teorema de Cauchy en
cierto intervalo
Entonces, si
También, si
y tales que
.
existe , también existirá
y además
entonces
Ejemplos:
Calculemos el
115
utilizando el teorema anterior.
Observe que
Luego:
Nota: Si
,
por lo que se tiene la forma
y las derivadas
satisfacen las
condiciones que se especificaron para las funciones y , según la hipótesis
de el teorema de la Regla de L'Hôpital, entonces puede aplicarse de nuevo la
Regla de L'Hôpital, obteniéndose que:
Puede operarse así sucesivamente siempre que se presente la forma
Ejemplos:
.
Calculemos los límites siguientes:
1.
Note que
aplicarse el teorema.
; se presenta la forma
y puede
Luego:
, aquí se presenta de nuevo la forma
que es posible aplicar otra vez el teorema.
Entonces:
116
por lo
2.
forma:
forma:
3.
117
forma:
Unidad VI
Sucesiones y
Series
6.1 Definición de sucesión.
Sucesión:
Se denomina sucesión a una función cuyo dominio es el conjunto de los
números naturales.
Para denotar el n-ésimo elemento de la sucesión se escribe an en lugar de f(n).
Ejemplo:
an = 1/n
a1 = 1, a2 = 1/2, a3 = 1/3, a4 = 1/4, ...
6.2 Límite de una sucesión.
El lím it e d e u na suce sió n es el núm e ro al cual se van aproximando los
términos de una sucesión.
a1= 1
a2= 0.5
a1000= 0.001
a1000 000 = 0.000001
El lím it e es 0 .
118
a 1 = 0.5
a 2 = 0 . 66 6 6. . . .
a 1 0 0 0 = 0 . 9 99 0 00 999 0 01
a 1000
000
= 0 .9 9 99 99 0 00 0 01
E l l í m i te e s 1 .
a1= 5
a2= 7
a 1 0 0 0 = 2 0 03
a 1000
000
= 2 0 0 0 00 3
Nin gú n n ú me ro sería e l l ím it e d e e sta su ce sión , e l l í m i te es
∞.
Lí m i te fi ni to de una s uce s i ón
Un a s u ce sió n a n t ie n e p o r l í m i te L si y só lo si p a ra cu alqu ie ra
n ú me ro p o sit ivo ε qu e t om em o s, e xist e un té rm in o a k , a pa rt ir
d e l c u a l t o do s lo s t é rm ino s d e a n , sigu ie n t e s a a k cu mp le n que
| a n −L| < ε.
L a su ce sió n a n = 1/ n t ien e p o r lím it e 0 .
S e p ue de d et e rm ina r a p a rt ir d e que té rm in o d e la su ce sió n , su
d is t a n c ia a 0 e s m e n o r qu e u n n ú me
ε ), rop opr o sit ivo (
p e qu e ño qu e é st e se a .
119
Co m o k >1 0 a p a rt ir d e l a 1 1 se cum p lirá qu e su d ista n cia a 0 e s
m e no r qu e 0. 1 .
V a mo s a d et e rm ina r a pa rt ir d e qu e t é rm ino la d ist a n cia a 0 es
m e no r qu e 0. 0 01 .
A p a rt ir d e l a 1 0 0 1 se cum p lirá qu e su d ista n cia a 0 es m en or
qu e 0 . 00 1 .
T am b ié n p o dem o s d ef in ir e l lím it e d e u n a su ce sió n m e d ia nte
e n t o rno s:
Un a s u ce sión a n t ie n e p o r l í m i te L si y só lo si p a ra cu a lqu ie r
e ntor no de L qu e t o mem o s, p o r pequ e ñ o qu e se a su ra d io ε,
e xis t e u n t é rm ino de la su ce sión , a pa rt ir d e l cu a l, lo s
s igu ie n t e s t é rm in os p e rt en e cen a d ich o en t o rno .
Lí m i te i nfi ni to de una s uc es i ón
Un a s u ce sión a n t ie n e po r l í m i te ∞+
cu a n d o p a ra tod a M>0
e xis t e u n t é rm in o a k , a p a rt ir d e l cu al t o d o s lo s t é rm in os d e a n ,
s igu ie n t e s a a k cum p len qu e a n > M.
E l lím it e d e la su ce s ió n a n = n 2 e s +∞.
1 , 4 , 9 , 1 6 , 2 5, 36 , 4 9 , . . .
120
S i M e s igu a l a 10 0 00 , su ra íz cu a d ra d a e s 1 0 0, po r t a n to a
p a rt ir d e a 1 0 1 sup era rá a 10 00 0 .
a 1 0 1 = 1 0 1 2 = 1 0 201
Un a s u ce sió n a n t ie n e p o r lím it e −∞ cu a n do p a ra tod a N >0
e xis t e u n t é rm in o a k , a p a rt ir d e l cu al t o d o s lo s t é rm in os d e a n ,
s igu ie n t e s a a k cum p len qu e a n < −N .
V a mo s a com p ro ba r qu e e l l í m i te d e la su ce sió n a n = −n
−∞.
2
es
−1 , −4 , −9 , −16 , −2 5 , −36 , −4 9, . . .
S i N = 1 0 00 0, su ra íz cu a d ra d a e s 1 0 0 , po r t an t o a pa rt ir de
a 1 0 1 s upe r ar á −1
a 0 00 0 .
a 1 0 1 = −1 0 1 2 = −1 0 2 0 1
6.3 Sucesiones monótonas y acotadas
Sucesión monótona creciente
Una sucesión es monótona creciente si se cumple que para todo n natural a n
<= a n+1 (a 1 <= a 2 <= a 3 <= ... <= a n ).
Ejemplo:
an = n es monótona creciente.
a1 = 1, a2 = 2, a3 = 3, a4 = 4, ...
121
Definición
Sucesión monótona decreciente
Una sucesión es monótona decreciente si se cumple que para todo n natural a n
>= a n+1 (a 1 >= a 2 >= a 3 >= ... >= a n ).
Ejemplo:
an = 1/n es monótona decreciente.
a1 = 1, a2 = 1/2, a3 = 1/3, a4 = 1/4, ...
6.4 Definición de serie infinita.
Límite infinito
lim a n = +inf <=> para todo K>0 existe N natural / para todo n > N a n > K.
Para cualquier número positivo K (tan grande como se quiera), podemos
encontrar un natural N, tal que aN y todos los términos siguientes son mayores
que K. Esto quiere decir que an puede hacerse mayor que cualquier cota, con
tal de que n sea lo suficientemente grande.
Del mismo modo se define lim a n = -inf <=> para todo K<0 existe N natural /
para todo n > N a n < K.
6.5 Serie aritmética y geométrica.
Serie aritmética
Suma indicada de todos los términos de una serie aritmética. Un ejemplo es el
siguiente:
1 + 2 + 3 + . . . + 100
La fórmula general para una serie aritmética es:
122
Sn = a1 + a2 + a3 + . . . + an
= a1 + (a1 + d) + (a1 + 2d) + . . . + [a1+(n-1)d]
= n(a1 + an)/2
= n[2a1 +(n-1)d]/2
En el ejemplo, el primer término, a1, es 1, y el último término, a100, es 100.
Utilizando la fórmula, la suma = 100(1+100)/2 = 5050.
Serie geométrica
Aquella cuyos términos forman una progresión geométrica. (Cada término es
igual al anterior multiplicado por una constante).
Si llamamos a al primer término y k a la constante,
Sn = a + ak + ak2 + ak3 + ... + akn-1 = Σ akn-1
Multipliquemos ambos miembros por k:
kSn = ak +ak2 + ak3 + ak4 + ... + akn = Σ akn
Restamos ambas ecuaciones:
Sn - kSn = a - akn
(a-akn)
Sn = ------(1-k)
a
akn
Sn = --- - --1-k 1-k
Para |k| < 1 lim Sn = a/(1-k) pues kn -> 0, la serie geométrica converge.
Para |k| > 1 la serie diverge pues kn -> inf.
Para |k| = 1 la serie diverge pues Sn = na.
Para |k| = -1 la serie es oscilante.
123
6.6 Propiedades de las series.
Unicidad del límite
Si
una
sucesión
H)
tiene
lim
límite
es
an
único.
=
b
T) b es único
Límite de la sucesión comprendida
Si una sucesión está comprendida entre otras dos que tienen igual límite,
entonces
H)
tiene
lim
Para
el
an
todo
n
=
>
mismo
lim
n0
límite.
bn
an
<=
=
cn
p
<=
bn
T) lim c n = p
Operaciones con límites
El límite de la suma, producto y cociente de sucesiones se determina por las
mismas
reglas
que
para
las
funciones
de
variable
continua.
Las
demostraciones son iguales, basta sustituir f(x) por an y considerar que la
tendencia siempre es hacia +infinito. Aquí sólo demostraremos el límite de una
suma. Para ver las demás reglas visitar la página sobre operaciones con
límites.
Límite de la suma
Si dos sucesiones tienen límite finito, entonces su suma tiene límite finito y es
igual
124
a
la
suma
de
esos
límites.
H)
lim
an
=
a,
lim
bn
=
b
T) lim a n + b n = a + b
Definición
Sucesiones equivalentes
Dos sucesiones se dicen equivalentes cuando el límite de su cociente es 1.
Definición
Sucesión acotada
M es cota superior de la sucesión a n si a n < M para todo n.
m es cota inferior de la sucesión a n
si a n
> m para todo n.
Una sucesión es acotada si tiene tanto cota superior como inferior.
Teorema
Toda
sucesión
monótona
H)
y
acotada
an
Existen
m
y
M
/
m
converge.
monótona
<
an
<
M
para
todo
n.
T) lim a n = b
Teorema
Toda
H)
T) a n acotada
125
sucesión
convergente
an
es
acotada.
convergente
6.7 Convergencia de series y divergencia.
Definición
Convergencia y divergencia
Cuando una sucesión tiene límite finito a se dice que es convergente y
converge
Una
sucesión
a
que
tiene
límite
infinito
a.
se
llama
divergente.
Una sucesión que carece de límite se llama oscilante.
La sucesión an = 1/n converge a 0.
La sucesión an = n2 es divergente.
La sucesión an = sen n es oscilante, pues sus valores varían entre 1 y -1.
FUENTES DE INFORMACIÓN
1. James – Stewart Cálculo de una variable. Edit. Thomson Editores.
2. Swokowski Earl W. Cálculo con Geometría Analítica. Grupo Editorial
Iberoamérica.
3. Roland E. Hostetler Robert P. Cálculo y Geometría Analítica Edit. McGrawHill.
4. Zill Dennis G. Cálculo con Geometría Analítica. Grupo Editorial Iberoamérica
5. Edwards Jr. C. H. y Penney David E. Cálculo y Geometría Analítica. Edit.
Prentice-Hall.
6. Fraleigh John B. Cálculo con Geometría Analítica. Edit. Addison- Wesley.
7. Anton Howard. Cálculo con Geometría Analítica Edit. Wiley.
8. The Calculus problem solver. Edit. R.E.A.
9. Leithold Louis. El Cálculo. Edit. OXFORD. University Press.
10. Swokowski Earl W. Álgebra y trigonometría con Geometría Analítica. Grupo
Editorial Iberoamérica
11. Granville William A. Cálculo Diferencial e Integral. Edit. Noriega – LIMUSA.
12. Thomas Jr- George / Finney Ross. CÁLCULO una variable. Edit, Pearson
Educativa.
126