UNIDAD II: TEMPERATURA Y GASES IDEALES

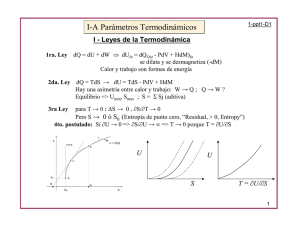
FISICA II 2010
TEMA IV
JUAN J CORACE
UNIDAD IV: PRIMER PRINCIPIO DE LA TERMODINÁMICA
Introducción. Trabajo y Calor. Conservación de la Energía. Interpretación molecular de los cambios energéticos.
Cantidades que pueden ser medidas. Expresión del primer principio para un sistema circulante. Propiedades de
la función Entalpía. La capacidad calorífica y la trayectoria. Relación de Mayer entre los calores molares de un
gas perfecto. Entalpía de los gases perfectos. Generalización del primer principio de la termodinámica aplicado a
sistemas abiertos. Consecuencias del Primer Principio de la Termodinámica
INTRODUCCIÓN
El primer principio de la Termodinámica expresa
principio general de conservación de la
energía. Este principio, es universalmente admitido y está en la base de todas las teorías
físicas. Puede enunciarse afirmando que la energía ni se crea ni se destruye, solamente se
transforma y se transmite.
Existen numerosas evidencias experimentales de la validez de este principio, que se
remontan a los inicios de la física. Desde un punto de vista termodinámico, debe mencionarse
el descubrimiento por Thomson de que el trabajo puede transformarse en calor, idea que fue
posteriormente cuantificada por Mayer y Joule.
Evidentemente, el principio de conservación se aplica indistintamente a todas las formas de
energía imaginables (energía eléctrica, química, etc.), pero nosotros, consideraremos
únicamente las energías almacenadas y en tránsito.
La Primera Ley de la Termodinámica es entonces el principio de conservación de la energía
aplicada a los sistemas. El sistema posee una energía intrínseca denominada energía
interna, que es una función de estado. Esta energía interna puede verse modificada por la
energía transferida como calor y/o trabajo con el medio.
Hay una analogía entre los
sistemas termodinámicos y los sistemas mecánicos conservativos, para los cuales se
cumple la ley de conservación de la energía (mecánica).
En un sistema mecánico conservativo se distinguen dos tipos de energía: cinética y
potencial, que se definen en términos de las velocidades y las posiciones de las partículas
que integran el sistema. La energía mecánica es la suma de ambas, y se mantiene
constante en ausencia de fuerzas exteriores que realicen trabajo sobre el sistema. Si hay
fuerzas externas, el incremento de la energía mecánica es igual al trabajo realizado sobre el
sistema por dichas fuerzas. La analogía consiste en imaginar que los sistemas
termodinámicos reales son sistemas mecánicos conservativos cuyas partes (átomos,
moléculas, etc.) son demasiado pequeñas como para ser percibidas. Se supone que si se
toman en cuenta los movimientos a escala microscópica, la ley de conservación de la
energía sigue valiendo, pero que las energías cinética y potencial asociadas con los
movimientos puramente microscópicos se manifiestan en la escala macroscópica del
experimento como calor. Luego, el calor es una forma de energía, y la energía (total) se
conserva.
I
FISICA II 2010
TEMA IV
JUAN J CORACE
TRABAJO Y CALOR
Ya hemos visto, en el tema I, que para que un sistema se encuentre en equilibrio
termodinámico, deben satisfacerse las siguientes condiciones:
•
Equilibrio mecánico: la fuerza ejercida por el sistema es uniforme y está equilibrada
por las fuerzas exteriores.
•
Equilibrio térmico: la temperatura del sistema es uniforme e igual a la del ambiente
•
Equilibrio químico: la estructura interna y la composición permanecen constantes
Una vez alcanzado el equilibrio termodinámico, y si el ambiente permanece invariable, no se
realizará ningún trabajo.
Si desde el ambiente se ejerce una fuerza sobre el sistema, ya no se cumple la condición de
equilibrio, lo que puede dar lugar a los siguientes fenómenos:
•
Las fuerzas dentro del sistema ya no serán uniformes y pueden producirse
turbulencias
•
Como resultado de estas turbulencias puede originarse una distribución no uniforme
de temperaturas, de manera que el sistema, globalmente, posea una temperatura
diferente a la del ambiente
•
El cambio en la distribución de fuerzas y de temperatura puede producir un estado
que no corresponde al equilibrio químico, y dar lugar a una reacción química.
TRABAJO
Desde el punto de vista mecánico, el trabajo W se define como el producto de la fuerza
aplicada (F) y el desplazamiento realizado (x):
W = F.x
En forma diferencial, un pequeño trabajo produce un pequeño desplazamiento:
ΔW = F. dx
El trabajo puede ser realizado por el sistema sobre el ambiente o por el ambiente sobre el
sistema; en ambos casos el trabajo fluye a través de la frontera. Por convención, cuando el
trabajo lo realiza el ambiente sobre el sistema, es positivo. Esto implica que un trabajo
positivo significa un flujo de energía hacia el sistema.
Supongamos que se tiene un gas encerrado en un cilindro, sobre el cual se tiene un pistón
que puede moverse libremente (sin rozamiento). Sobre este pistón se ejerce una fuerza
constante F, que producirá un desplazamiento del pistón una distancia dx, comprimiendo el
gas. En este caso, los alrededores están realizando un trabajo (trabajo de compresión)
sobre el gas.
II
FISICA II 2010
TEMA IV
JUAN J CORACE
Si A es el área de la sección transversal del cilindro y P la presión ejercida por el sistema
sobre el pistón, la fuerza sobre el pistón será P.A. Si como resultado de la presión ejercida,
el pistón se desplaza una distancia dx, el trabajo infinitesimal que realiza el sistema será:
ΔW = P.A.dx
Consideremos ahora el cambio de volumen del gas cuando el pistón lo comprime. Este
cambio en el volumen es -dV = A.dx, por lo que:
δW = -Pext.dV
Como dV es una cantidad negativa, dW > 0, y en la compresión de un gas fluye un trabajo
desde los alrededores hacia el sistema.
El trabajo en termodinámica se puede definir como la energía transferida entre un sistema y
su entorno por métodos que no dependen de la temperatura. La energía se transfiere en
este caso mediante fuerzas que ejerce el sistema sobre el entorno y viceversa.
CALOR
La forma más sencilla de definir el calor es por su habilidad de producir un cambio de
temperatura. Consideremos un sistema que absorbe calor de los alrededores. La cantidad
de calor absorbido, δQ, producirá un aumento de temperatura proporcional, que expresamos
como dT:
δQ = Cξ.dT
donde Cξ., la constante de proporcionalidad, es una característica del sistema llamada
capacidad calorífica.
Nótese que δQ > 0 cuando el sistema absorbe calor, es decir, se produce un aumento de la
temperatura del mismo. Es decir, todo flujo de energía hacia el sistema, ya sea como calor
o como trabajo, es positivo por convención.
Entonces Calor es la energía transferida entre un sistema y el entorno debido a la diferencia
de temperatura.
LA RELACIÓN ENTRE EL CALOR Y EL TRABAJO
III
FISICA II 2010
TEMA IV
JUAN J CORACE
El trabajo en termodinámica se puede definir como una interacción entre un sistema y su
ambiente con una transmisión de energía mecánica, sin variación de la temperatura. Si
existe variación de temperatura la interacción consiste en un flujo de calor.
Todo sistema posee asociado una energía que se denomina energía interna (U). El hecho
que distintas formas de energía puedan cruzar la frontera desde o hacia el sistema, indica
que el sistema varía su energía interna antes y después de llevar a cabo cierto proceso.
El aporte de energía al sistema producirá un aumento en su energía interna desde Ui hasta
Uf, tal que Uf > Ui. Si por el contrario el sistema cede energía al ambiente, la energía interna
del sistema disminuye, de manera que Uf < Ui. Como ya hemos visto, las formas en que
puede transferirse la energía entre el sistema y el ambiente es a través del pasaje de calor o
trabajo por la frontera.
Si bien la forma en que es transferida la energía depende de la trayectoria, la energía
interna no. La variación en la energía interna del sistema sólo depende de su valor en los
estados inicial y final, por lo tanto puede representarse matemáticamente por medio de una
función de estado. Puede, entonces, considerarse un sistema con una energía interna Ui
que cambia su valor por la transferencia de calor y/o trabajo. Toda forma de energía que
conduzca a una ganancia de energía por el sistema se considera, por convención, positiva.
De esta forma, la energía interna final del sistema, Uf, puede calcularse como:
Uf = Ui + Q + W
[4.1]
CONSERVACION DE LA ENERGIA.
FORMULACIÓN MATEMÁTICA DE LA PRIMERA LEY
Pasamos a considerar la formulación matemática del principio de conservación de la energía,
que es en definitiva el primer principio de la termodinámica. Para ello, distinguiremos entre
sistemas cerrados y sistemas abiertos. En cualquier caso, se trata de realizar un balance de
energías en el sistema considerado, de manera que la variación en la energía del sistema se
explica por la diferencia entre la energía que recibe y la energía que entrega. A este respecto,
es claro que, puesto que la energía ni se crea ni se destruye, no es posible que la energía
entregada por un sistema sea mayor que la energía que tenía inicialmente más la energía que
ha recibido. A un sistema así se le llama móvil perpetuo de primera especie, porque viola el
Primer Principio.
IV
FISICA II 2010
TEMA IV
JUAN J CORACE
Dado que la energía interna es una propiedad del sistema, es conveniente definir su
variación, más que su valor en un estado dado, de manera de tener presente que su valor
varía por los procesos que sufra el sistema. Definiendo la variación en la energía interna,
ΔU = Uf – Ui, la ecuación [4.1] puede expresarse como:
ΔU = Q + W
la expresión [4.2]
[4.2]
constituye la formulación matemática de la Primera Ley de la
Termodinámica. Considerando cambios muy pequeños (infinitesimales), el Primer Principio
se expresa como:
dU = δQ + δW
[4.3]
donde el símbolo δ da cuenta que se trata de una diferencial inexacta. Sin embargo, la
energía interna es una función de estado, y por lo tanto un cambio infinitesimal de la energía
interna es una diferencial exacta.
Por lo tanto, para poder pasar de un estado inicial a otro final, se producirán transferencias
de calor y de trabajo entre el sistema y el ambiente que dependen de la trayectoria, pero la
función U sólo depende de los estados inicial y final.
Durante el proceso de interacción, el sistema puede recibir calor o cederlo al ambiente.
Lo mismo ocurre con el trabajo. Para distinguir estas dos posibilidades se utiliza el siguiente
criterio de signos:
Concepto básico: La
transferencia térmica
neta es igual al
trabajo neto realizado
para un sistema que
experimenta un ciclo
PROPIEDADES DE LA ENERGÍA INTERNA
Partiendo de la expresión [4.3]
dU = δQ + δW
V
FISICA II 2010
TEMA IV
JUAN J CORACE
si V = CTE δW = 0
que nuestra expresión reducida a: δQ = dU
la energía interna es función de la temperatura y el volumen,
U = f(T;V)
⎛ ∂U ⎞
⎛ ∂U ⎞
dU = ⎜
⎟ dV ; Como V = CTE el segundo término del segundo miembro es
⎟ dT + ⎜
⎝ ∂T ⎠ T
⎝ ∂V ⎠V
igual a cero, por lo tanto:
⎛ ∂U ⎞
⎛ ∂U ⎞
dU = ⎜
⎟ dT ; igualando con la expresión reducida δQV = ⎜
⎟ dT
⎝ ∂V ⎠V
⎝ ∂V ⎠V
Por lo tanto
δQV
⎛ ∂U ⎞
=⎜
⎟
dT ⎝ ∂V ⎠V
⎛ ∂U ⎞
CV = ⎜
⎟
⎝ ∂V ⎠V
[4.4]
ANALOGÍA DEL PRIMER PRINCIPIO CON LA ECONOMÍA
Una analogía propuesta por Eisenberg y Crothers permite un entendimiento del Primer
Principio de la Termodinámica.
Supongamos que tenemos una cierta cantidad de fondos
que llamaremos energía, en el Banco que llamaremos
sistema. Estos fondos lo
emplearemos para pagar (transferencia de energía desde el sistema al ambiente) a
nuestros acreedores (ambiente). La forma de pago, podrá ser en efectivo (trabajo) o con
cheques (calor).
A su vez, cada uno de los pagos lo podremos hacer en una sola entrega o en cuotas, por lo
que la forma de pago dependerá del número de cuotas (trayectoria reversible o
irreversible). Sin embargo, el balance monetario de nuestra cuenta (ΔU) nos dirá la
diferencia antes y después de realizar los pagos, independientemente de la forma en que lo
hemos hecho.
INTERPRETACIÓN MOLECULAR DE LOS CAMBIOS ENERGÉTICOS
VI
FISICA II 2010
TEMA IV
JUAN J CORACE
La formulación del Primer Principio de la Termodinámica no requiere del conocimiento de la
forma en que es almacenada la energía. Los Principios de la Termodinámica realizan una
descripción
macroscópica
del
Universo,
prescindiendo
del
conocimiento
a
nivel
microscópico. Sin embargo, es útil tener un conocimiento mínimo de las formas en que la
energía es almacenada en los sistemas, de manera de poder razonar los efectos que los
diferentes cambios energéticos tendrán en un sistema.
El Primer Principio de la Termodinámica nos dice que la cantidad de calor y de trabajo que
se transfiere al sistema aumentará su energía interna. La forma en que esa energía es
almacenada por el sistema requiere de la consideración de la naturaleza molecular del
sistema. La energía transferida se almacena como energía cinética (Ec) en las moléculas, y
produce un aumento de la energía potencial (Ep) que surge de la interacción entre ellas.
La Energía cinética es responsable del movimiento de las moléculas. Para el caso de un
gas perfecto monoatómico, se considera que el sistema está formado por átomos puntuales
que no interactúan entre ellos, y que obedecen a la ecuación del gas perfecto. Cuando a
este tipo de sistema se le transfiere energía, la misma es almacenada como energía cinética
en su totalidad, no existiendo interacción entre los átomos. Esta energía cinética puede
calcularse como:
EC =
3
nRT
2
Esta ecuación predice que al aumentar la temperatura de un gas perfecto monoatómico,
aumentará la energía cinética debido al mayor movimiento de las partículas. También
predice que para el cero absoluto (T = 0 K), las partículas no se moverán pues la energía
cinética de las mismas es nula. Finalmente, toda la energía transferida a este tipo de gas,
ya sea como calor o como trabajo, producirá un aumento de la temperatura.
Las sustancias reales interaccionan entre sí, y por lo tanto existe una cierta energía
potencial asociada a esa interacción. Supongamos que se quiere fundir un sólido. Para ello
sabemos que debemos aumentar la temperatura. Este aumento de la temperatura producirá
un aumento de la energía cinética de las partículas. Sin embargo, este aumento es muy
pequeño debido a que los átomos en las fases condensadas se mueven a una velocidad
similar. Por lo tanto, la energía transferida (en este caso como calor) se utiliza para separar
las moléculas entre sí aumentando la energía potencial que las mantiene unidas, debilitando
las fuerzas que las unen, y produciendo el cambio de fase.
CANTIDADES QUE PUEDEN SER MEDIDAS EN TERMODINÁMICA
VII
FISICA II 2010
TEMA IV
JUAN J CORACE
Antes de aplicar el Primer Principio de la Termodinámica a sistemas precisos, veremos qué
cantidades pueden ser medidas para poder aplicarlo. Las cantidades que debiéramos poder
medir para aplicar este Principio serían la variación de la energía interna (ΔU), el trabajo (W)
o el calor (Q). Sin embargo, como ya hemos visto, el calor y el trabajo son cantidades que
dependen de la trayectoria, es decir, de cómo son transferidos a través de la frontera. En
otras palabras, se puede lograr el mismo efecto (un determinado valor para la variación en la
energía interna) transfiriendo calor y trabajo por infinitas trayectorias. Por lo tanto, la medida
de la energía interna sólo puede realizarse fijando las trayectorias por las que la energía es
transferida.
PRIMERA LEY APLICADA A UN CICLO
Una vez estudiados los conceptos de trabajo y calor, estamos listos para presentar la
primera ley de la termodinámica. Históricamente la primera ley se expresó para un ciclo: la
transferencia térmica neta es igual al trabajo neto realizado para un sistema que
experimenta un ciclo. Esto se expresa en forma de ecuación:
∑W = ∑ Q
donde el símbolo
∫
o
∫ δW = ∫ δQ
implica una integración alrededor de un ciclo completo.
¿Pero que es un ciclo? Un ciclo resulta cuando un sistema experimenta dos o más procesos
y regresa al estado inicial. Esto se puede ilustrar de la siguiente manera:
Supongamos un peso unido a un montaje de polea y rueda de paletas, supongamos que el
peso G baja cierta distancia, con lo que realiza trabajo sobre el sistema contenido en el
tanque que ilustra la figura, este trabajo es igual al peso por la distancia que baja. La
temperatura del sistema (fluido en el tanque) subirá de inmediato una cantidad ΔТ. Ahora,
el sistema regresa a su estado inicial (para completar el ciclo) al transferir calor al entorno.
Esto reduce la temperatura del sistema a su temperatura inicial. La primera ley expresa que
esta transferencia térmica será exactamente igual al trabajo que fue realizado por el peso
que baja.
PRIMERA LEY APLICADA A UN PROCESO
VIII
FISICA II 2010
TEMA IV
JUAN J CORACE
La primera ley de la termodinámica se aplica con frecuencia a un proceso cuando el sistema
cambia de un estado a otro Podríamos considerar un ciclo compuesto de los dos procesos
representados por A y B en la siguiente figura:
Si se aplica la primera ley a este ciclo:
2
1
2
1
1
2
1
2
2
2
2
2
1
1
1
1
∫ δQ A + ∫ δQB = ∫ δW A + ∫ δWB
∫ δQ A − ∫ δQB = ∫ δW A − ∫ δWB
2
2
1
1
∫ δ (Q A − W A ) = ∫ δ (QB − WB )
Esto es, el cambio en la cantidad Q – W del estado 1 al estado 2 es igual a lo largo de la
trayectoria A, que a lo largo de la trayectoria B, como este cambio lo expresamos:
δQ - δW = dU
TRANSFERENCIA DE TRABAJO A PRESIÓN CONSTANTE
Consideremos la expansión de un gas contra una presión constante. Este proceso se
esquematiza en el siguiente diagrama P-V, donde se dibujan dos isotermas, T1 y T2. El gas
se encuentra inicialmente a una presión Pext, constante, ocupando un volumen V1 a una
temperatura T1.
IX
FISICA II 2010
TEMA IV
JUAN J CORACE
Cuando el gas se expande contra la misma presión (Pext) hasta un volumen final V2, el
mismo se calienta, alcanzando la temperatura T2. En primer lugar, analizaremos la forma de
cálculo del trabajo. De acuerdo con la definición de trabajo:
δW = -Pext.dV
Expresión que podremos integrar una vez que fijemos la trayectoria para el proceso. En
nuestro caso, se trata de una expansión a presión constante, por lo cual:
V2
W = − Pext ∫ dV
[4.5]
V1
donde la Pext queda fuera de la integral por tener un valor constante constante. La expresión
final para el trabajo es:
W = − Pext (V2 − V1 ) = − Pext ΔV
[4.6]
En primer lugar notaremos que como V2 > V1, ΔV > 0, por lo que el trabajo realizado
durante la expansión a presión constante es negativo. Esto tiene sentido, pues el trabajo fue
realizado contra el medio, lo que implicó que el sistema empleara parte de su energía
interna para realizarlo.
Por último, cabría preguntarse por qué aumenta la temperatura del sistema. Como el mismo
debe aumentar su volumen manteniendo la presión constante, las partículas que lo forman
deberán aumentar su movimiento de manera de mantener el número de choques por unidad
de superficie (presión). Como lo hemos mostrado en el Tema 2, el aumento de movimiento
de las partículas se encuentra asociado a una mayor temperatura.
TRANSFERENCIA REVERSIBLE DE TRABAJO A TEMPERATURA CONSTANTE
Consideremos ahora la misma expansión de un gas desde V1 hasta V2, pero a través de una
trayectoria reversible. Esto implica que la presión externa diferirá infinitesimalmente de la
presión interna del gas. Por otra parte, si esta trayectoria se lleva a cabo a temperatura
constante, el sistema se estará moviendo a lo largo de una isoterma en el diagrama P – V.
De acuerdo con lo que se desprende de la inspección de este diagrama, la expansión
reversible e isotérmica de un gas producirá una disminución de la presión.
A continuación calcularemos el trabajo. Nuevamente, partiendo de la definición:
δW = -Pext.dV
[4.7]
impondremos la trayectoria para poder integrarla. Puesto que en todo momento, la presión
externa y la presión del gas difieren infinitesimalmente, se puede considerar que Pgas ≅ Pext
X
FISICA II 2010
por lo que
TEMA IV
δW = -Pgas.dV
JUAN J CORACE
[4.8]
Por último, falta expresar la presión del gas en función de las propiedades del mismo, esto
es, sustituir su valor por una ecuación de estado. Consideraremos como admitido el modelo
del gas perfecto, por lo que la presión del gas queda expresada como:
como:
P=
nRT
V
[4.9]
y sustituyendo en [4.8] e integrando:
V2
nRT
dV
V
V1
W = −∫
Si el proceso se lleva a cabo isotérmicamente:
V2
dV
V
V1
W = − nRT ∫
W = − nRT ln
V2
V1
[4.10]
Resumiendo, establecimos una forma de cálculo para el trabajo de expansión que realiza el
sistema sobre el ambiente para las siguientes condiciones experimentales:
1) gas considerado como un gas perfecto,
2) temperatura constante y
3) trayectoria reversible.
La trayectoria reversible nos ha permitido considerar que la presión exterior varía de la
misma forma que la presión del gas, y la ecuación de estado derivada para el gas perfecto
nos ha dado la relación necesaria entre las propiedades del sistema.
XI
FISICA II 2010
TEMA IV
JUAN J CORACE
Al igual que con el cálculo para el trabajo realizado contra una presión constante,
verificamos que el trabajo de expansión es negativo, lo que de acuerdo con la convención
de signos implica que el sistema ha perdido parte de su energía interna.
Por último cabe considerar una situación especial. ¿Cuál es la magnitud del trabajo que se
realiza siguiendo una trayectoria de volumen constante? De acuerdo con la definición de
trabajo, es fácil deducir que un cambio en el estado del sistema que no implique un cambio
de volumen no tiene involucrado ningún trabajo, es decir, que para que el sistema transfiera
trabajo, ya sea que lo ceda o que lo reciba, debe cambiar su volumen.
EL TRABAJO NO ES UNA FUNCION DE ESTADO
Podemos observar que existen diferentes caminos o trayectorias para acceder a un punto
determinado; por ejemplo si partimos de un estado inicial “i” con coordenadas (Pi:Vi) y
pretendemos llegar a otro estado final “f” de coordenadas (Pf:Vf); podemos hacerlo por el
camino A, es decir a volumen constante (isócora) hasta el punto A, y luego a partir de este
punto a presión constante (isobara) hasta el estado final, el área sombreada representa el
trabajo realizado desde “i” hasta “f”. O bien hacerlo por los caminos B o C
f
W A = − Pf ( v f − v i )
W B = − Pi (v f − vi )
WC = − ∫ Pdv
i
W A ≠ WB ≠ WC
TRANSFERENCIA DE CALOR A VOLUMEN CONSTANTE
Supongamos que tenemos un recipiente con un gas, sistema A, al cual le transferimos calor
mediante una resistencia eléctrica. Además de aumentar su temperatura, el gas se expande,
realizando un trabajo en contra del ambiente. Podemos impedir que se realice este trabajo si
mantenemos constante el volumen.
XII
FISICA II 2010
TEMA IV
JUAN J CORACE
De acuerdo con el Primer Principio de la Termodinámica, el calor
transferido se utilizará totalmente en variar la energía interna del
sistema, pues al impedir el aumento de volumen del gas, el término
que toma en cuenta al trabajo, δW, vale 0. De esta manera, la
expresión para el Primer Principio de la Termodinámica, cuando se
transfiere calor a volumen constante, toma la forma:
[4.11]
dU = dQv
donde Qv indica que el calor fue transferido a volumen constante. Obsérvese que el símbolo
δ para la diferencial se ha sustituido por d, indicando que cuando se fija la trayectoria para la
transferencia de calor, la diferencial dQv es una diferencial exacta, y por lo tanto el calor en
estas condiciones es una función de estado.
Una vez establecido que el calor transferido a volumen constante es una función de estado,
podemos considerar un cambio finito:
[4.12]
ΔU = Qv
La ecuación [4.12] nos indica una forma experimental para obtener el cambio en la energía
interna de un sistema, esto es, midiendo el calor transferido a volumen constante.
TRANSFERENCIA DE CALOR A PRESIÓN CONSTANTE
Retornemos a nuestro ejemplo del recipiente con el gas que hemos calentado, pero no
vamos a impedir que se realice el trabajo contra el ambiente, es decir, permitiremos que el
gas se expanda libremente debido al aumento de la temperatura. En este caso ya no es
válida la ecuación [4.12]; pues el sistema aumenta su energía debido al calor absorbido,
pero pierde parte de esta energía adquirida en realizar trabajo sobre el ambiente. Aplicando
el Primer Principio de la Termodinámica, la variación en la energía interna será:
dU= δQ + δW
[4.13]
Para poder llevar a cabo esta conjetura, debemos imponer una trayectoria. Si la expansión
del gas de nuestro ejemplo se lleva a cabo contra la atmósfera, la presión es constante e
igual a la Pext; entonces:
δW = dW = - Pext dV
y la variación del calor transferido a presión constante será:
dQP = dU +PextdV
[4.14]
donde QP indica que el calor ha sido transferido a presión constante. Obsérvese que
nuevamente sustituimos el símbolo δ para la diferencial por d, indicando que cuando el
calor es transferido a presión constante, es una función de estado. Esto se debe a que QP
XIII
FISICA II 2010
TEMA IV
JUAN J CORACE
resulta ser la suma de dos funciones de estado, y por lo tanto se trata de una función de
estado también.
Aplicando el Primer Principio de la Termodinámica a un sistema sobre el que se lleva a cabo
un proceso a presión constante, hemos obtenido entonces una función de estado para el
calor, que toma en cuenta tanto la variación en la energía interna del sistema como el
trabajo realizado. Puesto que QP es una función de estado, se trata de una propiedad del
sistema, y por lo tanto vale la pena definir esta nueva propiedad. A esta nueva propiedad se
le denomina entalpía, H, y corresponde al calor transferido a presión constante:
H = U + PV
La razón por la que vale la pena definir esta nueva propiedad es que puede ser medida
experimentalmente: basta con medir el calor transferido a presión constante.
Y teniendo en cuenta que la entalpía es una función de estado, la expresión para la entalpía
para un cambio finito es:
ΔH = ΔU +PΔV
[4.15]
EXPRESION DEL PRIMER PRINCIPIO PARA UN SISTEMA CIRCULANTE
Si tenemos un sistema como el de la figura, donde en la sección 1-1 de entrada ingresa un
caudal o gasto G , tal que al egresar por la sección 2-2 sea el mismo; G1 = G2= G; es decir
a régimen permanente, y sean p1, c1, z1 y u1, la presión , velocidad, la altura y la energía
interna respectivamente en la entrada; y p2,c2, z2 y u2, en la salida
podemos es escribir; (que expresamos directamente en términos de magnitudes específicas):
Q = E2 – E1 + W + WC
Donde
E1= u1 + ½ c12+g z1
W = W1 – W 2
con W1 = - p1v1
[4.16]
E2= u2 + ½ c22+g z2
y
y W2 = p2v2
Reemplazamos en la expresión [4.16]
Q = u2 + ½ c22+g z2 – (u1 + ½ c12+g z1 ) - p1v1 + p2v2 + WC
XIV
FISICA II 2010
TEMA IV
JUAN J CORACE
Agrupando a ambos lados subíndices iguales:
Q + u1 + ½ c12+g z1 + p1v1 = u2 + ½ c22+g z2 + p2v2 + WC
Donde el término de la izquierda representa la energía entrante, y el término de la derecha
la energía saliente. Si ordenamos convenientemente cada término:
u1 +p1v1+ ½ c12+ g z1 + Q = u2 + p2v2 + ½ c22+g z2 + WC
Como h = u +pv; quedará la expresión:
h1 + ½ c12+ g z1 + Q = h2 + ½ c22+g z2 + WC
Haciendo Q = (h2 – h1) + ½
(c22
-
c12)
[4.17]
+g(z2 – z1) + WC
En el caso particular que ΔEC = 0 y ΔEP = 0
Q = (h2 – h1) + WC
δQ = dh + δWC
Si h = u +pv
[4.18]
dh = du +pdv + vdp
du +pdv = δQ entonces dh = δQ + vdp o bien δQ = dh – vdp
Concepto básico:
La
entalpía
es
simplemente
una
combinación
de
propiedades
Reemplazo esta última expresión en [4.17]
dh – vdp = dh + δWC y nos queda:
δWC = – vdp; integrando esta última expresión
2
WC = ∫ − vdp
[4.19]
1
PROPIEDADES DE LA FUNCION ENTALPIA
Hemos obtenido la expresión:
Q = H2 - H1 + WC
Si Q= 0
WC = H2 – H1
Para el caso de un sistema cerrado,
δW = pdv y δQ = du +pdv
Como H = U +PV; dH = dU +PdV +VdP
Por lo que dH = δQ +VdP
En el caso que dP sea igual a cero, es decir a P= CTE; dHP = δQP;
e integrando obtenemos
QP = H2 – H1
XV
FISICA II 2010
TEMA IV
JUAN J CORACE
δQP = CPdT; → CP =dT /dQP
como H= f(P;T)
⎛ ∂H ⎞
⎛ ∂H ⎞
dH = ⎜
⎟ dP + ⎜
⎟ dT ; Como P = CTE
⎝ ∂P ⎠ T
⎝ ∂T ⎠ P
⎛ ∂H ⎞
dH = ⎜
⎟ dT ; y dH P = ∂QP
⎝ ∂T ⎠ P
Nos queda
∂QP ⎛ ∂H ⎞
⎛ ∂H ⎞
=⎜
⎟
⎟ es decir C P = ⎜
dT
⎝ ∂T ⎠ P
⎝ ∂T ⎠ P
LA CAPACIDAD CALORÍFICA Y LA TRAYECTORIA
Hemos visto que cuando se fijan las trayectorias, el calor transferido es una propiedad del
sistema. La definición de calor varía de acuerdo con la trayectoria en que se realiza el
proceso, y tendremos entonces:
dQV = CVdT
[4.20]
dQP = CPdT
[4.21]
y
donde las capacidades caloríficas son diferentes, y los subíndices indican las condiciones
(trayectorias) en las que se realiza el proceso de transferencia de calor.
De acuerdo con las anteriores ecuaciones, podemos dar una definición específica para las
capacidades caloríficas a presión constante y a volumen constante:
CV =
dQV ⎛ ∂U ⎞
=⎜
⎟
dT
⎝ ∂T ⎠V
[4.22]
CV =
dQ P ⎛ ∂H ⎞
=⎜
⎟
dT
⎝ ∂T ⎠ P
[4.23]
y
Las capacidades caloríficas CV y CP expresan la cantidad de calor requerida para aumentar
la temperatura de una cierta cantidad de sustancia en 1 grado en procesos llevados a cabo
a volumen o presión constante, respectivamente. La cantidad de sustancia puede ser
expresada en gramos (calor específico) o en moles (capacidad calorífica molar). Para una
misma sustancia, las capacidades caloríficas CP y CV son diferentes, pues a presión
constante, parte del calor es utilizado en realizar trabajo.
XVI
FISICA II 2010
TEMA IV
JUAN J CORACE
RELACIÓN DE MAYER ENTRE LOS CALORES MOLARES DE UN GAS PERFECTO
Supongamos un mol de un gas perfecto contenido en un cuerpo de bomba cuyo émbolo se
deja libre, no se quitan ni añaden pesas. La presión permanece constante. El calor
suministrado al gas en estas condiciones se emplea en aumentar el volumen y la
temperatura.
PV = RT ⇒ PdV = RdT
⇒ dU = CVdT (ley de Joule)
δWexp = - PdV = - RdT
⇒ Si P = cte ⇒ CP= (δQ/dT)P ⇒δQ = CP.dT
Aplicamos el primer principio:
dU = δQ + δW
dU = CV dT
δQ= CP dT
δW= - R dT
CV dT = CP dT - R dT
R = CP - CV
[4.24]
Expresión esta que recibe el nombre de relación de Mayer, si generalizamos para un gas
ideal:
n R = CP - CV
ENTALPIAS DE LOS GASES PERFECTOS
Sea un sistema formado por un conducto en el cual se intercala un medio o tapón poroso
poroso, tal que quedan definidas dos secciones caracterizadas por sus propiedades:
XVII
FISICA II 2010
TEMA IV
JUAN J CORACE
Partiendo de la expresión [4.17]
h1 + ½ c12+ g z1 + Q = h2 + ½ c22+g z2 + WC
si Q = 0 considerando el sistema aislado y siendo WC = 0 porque no se transfiere Energía
Mecánica y considerando z = 0 (conducto horizontal); la expresión [4.17] queda reducida a:
h1 + ½ c12 = h2 + ½ c22 ; en el caso que c1 = c2
por ser ambas secciones iguales,
h = f(T)
dHP = CPdT integrando entre T1 y T2
T2
h2 − h1 = ∫ C P dT
[4.25]
T1
Si el gas es «real»; T1 ≠ T2 el efecto del tapón poroso sería frigorífico si T2 < T1; o calorífico
si T2 > T1; dependiendo de los valores de la presión.
GENERALIZACION DEL PRIMER PRINCIPIO APLICADO A SISTEMAS ABIERTOS
Estos sistemas denominados “abiertos” intercambian energía no sólo en forma de calor y trabajo,
sino también en forma de trabajo de flujo o de circulación (necesario para que entre y salga
masa del sistema), y pueden en principio almacenar energía en cualquiera de las formas que
vimos. Al hacer el balance energético del sistema debemos de tener en cuenta, además de los
términos ya considerados para sistemas cerrados (energía interna, calor y trabajo) los siguientes
(que expresamos directamente en términos de magnitudes específicas):
• Trabajo de flujo: wf = Δ(pv)
• Incremento de energía cinética: ΔEC= Δ(1/2 c2)
• Incremento de energía potencial ΔEP= Δ(gz)
De esta manera, para un proceso finito, tendremos el siguiente balance:
Δ(u +1/2 c2 +gz)= q-w s -w f
donde hemos agrupado en el miembro izquierdo todos los términos de almacenamiento de
energía, mientras que en el miembro derecho hemos agrupado los términos de energía en
tránsito, desdoblando el trabajo total en el trabajo útil ws y el trabajo de flujo wf
w = ws + w f
Teniendo en cuenta la expresión del trabajo de flujo, puede cambiarse de miembro e introducirlo
bajo el signo incremental, obteniéndose
Δ(u +pv +1/2 c2 +gz)= q-w s
y recordando la definición de entalpía, h = u + pv, se obtiene finalmente:
Δ( h +1/2 c2 +gz)= q-w s
[4.26]
expresión válida del Primer Principio para sistemas abiertos en un proceso finito.
XVIII
FISICA II 2010
TEMA IV
JUAN J CORACE
En el caso de un proceso elemental tendremos:
dh +1/2 dc2 +d(gz)= δ q- δ w s
Consideremos el caso de un proceso cuasiestático, en que δw = pdv. Entonces, como δw =
δws + δwf sustituyendo:
pdv = pdv + vdp + δ ws
y por tanto la expresión del trabajo útil es
δ ws = - vdp
[4.27]
PRIMERA LEY APLICADA A VOLÚMENES DE CONTROL
Consideremos un volumen de control fijo como el de la figura donde,
Q – W = ΔΕsist
La primera ley puede escribirse de la siguiente manera:
Q – W = ΔΕc + ΔΕp + ΔH
Si m = ρΑc;
y Δm =m1 - m2; masa entrante y
saliente, respectivamente.
El
flujo
se
considera
uniforme,
velocidad, la presión y
cuando la
la densidad son
constantes en el área de la sección transversal.
El flujo se considera estacionario, cuando
las
variables de flujo no cambian con el tiempo.
la ecuación de la energía en el caso de flujo estacionario (las variables de flujo no cambian
en el tiempo), que es el caso de la mayor parte de problemas de volumen de control:
1 2
⎡
2 ⎤
Q& − W& S = m& .⎢h2 − h1 + g ( z 2 − z1 ) + (c2 − c1 )⎥
2
⎣
⎦
[4.28]
& representan:
Donde Q& , W& S y m
Q
Q& =
Δτ
W
W& S = S
Δτ
y
m& =
m
Δτ
Cuando los cambios de energía cinética y energía potencial son insignificantes:
Q& − W& S = m& .(h2 − h1 )
[4.29]
NOTA: El punto indicado sobre la variable indica una cantidad por unidad de tiempo, flujo o gasto.
XIX
FISICA II 2010
TEMA IV
JUAN J CORACE
CONSECUENCIAS DEL PRIMER PRINCIPIO
Durante los años 1840-1878, J.P. Joule llevó a cabo una serie de cuidadosos experimentos
sobre la naturaleza del calor y el trabajo, que fueron fundamentales para entender la primera
ley de la Termodinámica y el concepto de energía Para ello colocó cantidades medidas de
agua en un contenedor aislado y la agitó mediante un agitador rotativo; la cantidad de trabajo
transmitida al agua por el agitador se midió con toda precisión y se anotaron cuidadosamente
los cambios de temperatura experimentados por el agua, descubriendo que se requería una
cantidad fija de trabajo por unidad de masa de agua, porcada grado que aumentaba su
temperatura a causa de la agitación, y que la temperatura original del agua se podía restaurar
por transferencia de calor mediante el simple contacto con un objeto más frío, demostrando la
existencia de una relación cuantitativa entre el trabajo y el calor y, por lo tanto, que el calor era
una forma de energía. En experimentos semejantes se aplicó energía al agua en forma de
trabajo, pero se extrajo de ésta en forma de calor; la energía una vez aplicada al agua como
trabajo y antes de extraerla como calor, quedó almacenada en el agua en otra forma, ni calor
ni trabajo, a la que se definió como energía interna U.
La energía interna de una sustancia no incluye las energías potencial y cinética asociadas a
una sustancia como resultado de las interacciones entre sus campos de fuerza y su posición
espacial (energía potenciado de su movimiento macroscópico (energía cinética), que son
formas extremas de energía; la energía interna se refiere a la energía de las moléculas
constitutivas de la sustancia, que se encuentran en movimiento continuo y poseen energía
cinética de traslación y (a excepción de las moléculas monoatómicas) energía cinética de
rotación y vibración interna. La aplicación de calor a una sustancia incrementa esta actividad
molecular por lo que origina un aumento en su energía interna; el trabajo realizado sobre una
sustancia puede tener el mismo efecto, como demostró Joule.
El Primer Principio de la Termodinámica no puede demostrarse teóricamente, pero sí
experimentalmente, como hemos visto; el axioma fundamental que sirve para establecerlo,
dice:
LA ENERGÍA INTERNA ES UNA PROPIEDAD TÉRMICA DE LA MATERIA, por lo que siempre que
un sistema incremente su energía, aparece en otro sistema la correspondiente
disminución de la misma, es decir, se establece una conservación de la energía que
constituye la esencia del postulado del Primer Principio de la Termodinámica.
LA ENERGÍA NI SE CREA NI SE DESTRUYE, SOLO SE TRANSFORMA, que también se puede
expresar como, La cantidad de energía en el Universo sólo puede modificarse por un cambio
equivalente en la cantidad de materia, según la expresión:
ΔE = Δm c2
siendo c la velocidad de la luz.
XX
FISICA II 2010
TEMA IV
JUAN J CORACE
Este Principio establece la imposibilidad de la existencia del móvil perpetuo de primera especie,
es decir, ninguna máquina puede producir un trabajo sin el correspondiente consumo de energía.
Para que se cumpla este Principio en todas las transformaciones, reales o ideales,
perfectas o imperfectas, tiene que existir un balance de energía entre el sistema y el medio
exterior:
ΔEmedio exterior + ΔEsistema = 0
[4.30]
El Primer Principio no proporciona ninguna idea sobre si una transformación se ha
realizado o no completamente; la variación de la energía ΔEsistema puede ser debida a
cambios en su energía interna, en sus energías cinética y potencial globales o en partes
finitas de dicho sistema.
El intercambio de energía con los alrededores ΔEmedio exterior puede ser debido al aumento o
disminución de varias formas de energía, cuyas variaciones pueden estar motivadas por
tres causas:
a) Transferencia de masa, b) Transferencia de calor, c) Transferencia de trabajo
Cuando la energía se transmite en forma de calor o de trabajo, generalmente no se
suele medir, debido a dificultades inherentes a los aparatos de medida. Desde el punto de
vista del balance de energía en el sistema cerrado, se presenta el inconveniente de que
sólo se pueden evaluar satisfactoriamente aquellos procesos que se efectúan muy
lentamente, por lo que el estudio del sistema cerrado se reduce muy a menudo al de un
sistema en equilibrio; por el contrario, la definición de sistema abierto amplía el campo
termodinámico, de forma que pueden medirse perfectamente aquellas transformaciones
en las que existen flujos de materia.
EL PRIMER PRINCIPIO Y LOS SISTEMAS CERRADOS
El balance de energía dado por el Primer Principio constituye únicamente un paso en el
desarrollo de expresiones matemáticas entre las propiedades de equilibrio de la materia en
reposo en régimen estacionario.
Energía de un sistema cerrado - En un sistema cerrado como el indicado en la Fig. V.l, un
elemento de masa Δm posee una energía interna específica u y puede tener también una
energía potencial específica z y una energía cinética específica c2/2g. La energía
específica total e en un punto M del sistema, y en un instante t determinado, viene dada
por:
e=u+
c2
+z
2g
[4.31]
Como la energía que posee un elemento puede ser distinta de la que posean los
elementos que le rodean, especialmente cuando se está realizando una transformación,
XXI
FISICA II 2010
TEMA IV
JUAN J CORACE
en un momento determinado t la energía total del sistema viene dada por la integral de
volumen:
∫ edm = ∫ eρdV
vol
vol
en la que hay que hacer notar que tanto e como el producto (ρe) pueden ser función del
tiempo y de la posición, mientras que Etotalsistema es únicamente función del tiempo.
Cuando e varía con la posición de un modo desordenado, en los sistemas que no han
alcanzado el equilibrio, (transformaciones dinámicas), no se puede utilizar la ecuación
energética anterior para calcular la energía del sistema Esistema, pero si el sistema está en
equilibrio termodinámico, o en una posición próxima a él, (al comienzo y al final de la
transformación), o si se utilizan valores medios de ρ, u, c y z, se puede integrar la ecuación
energética anterior, obteniéndose:
Etotalsistema = U + m
c2
+ mz
2g
[4.32]
que representa la energía del sistema en un momento determinado, mientras que ΔEsistema
indica la variación exacta que experimenta la energía en el intervalo de tiempo comprendido
entre t1 y t2,
BALANCE DE ENERGÍA DE UN SISTEMA ESTACIONARIO
El balance de energía entre un sistema y el medio que le rodea se expresa en la forma:
ΔEmedioexterior + AEsistema = 0
;
ΔEmedioexterior = - ΔEsistema = 0
en la que intervienen únicamente propiedades del sistema; sustituyendo el valor del
incremento de energía del medio exterior por los conceptos de calor y trabajo
intercambiadas con el medio exterior Q (t) y T (t), obtenidas por integración en toda la
superficie del sistema, entre los tiempo t1 y t2, el balance exacto de energía se puede
poner en la forma:
t1 → t 2
t1 → t 2
t1 → t 2
− ΔE medioexterior = ΔQ Superficie
− ΔW Superficie
= ΔE Sistema
XXII
FISICA II 2010
TEMA IV
JUAN J CORACE
que se realiza únicamente sobre el sistema y es la ecuación general de la energía para un
sistema cerrado. Como el tiempo es la variable independiente, dividiendo la anterior por Δt :
ΔQ Δ W Δ E
y en el límite para Δt→0
=
−
Δt
Δt
Δt
dQ dW dE
=
−
dt
Δt
Δt
Multiplicando por Δt; se obtiene:
dQ
dW
dE
Δt −
Δt =
Δt
dt
Δt
Δt
Que es por definición, la diferencial de una variable dependiente:
dQ - dW = dE
[4.33]
que se puede poner también en la forma:
dW = dQ − (dU + d (m
c2
) + zdm
2g
en donde todo el trabajo desarrollado por el sistema cerrado no tiene por qué ser trabajo útil
o disponible; si una fracción del mismo se utiliza en vencer la resistencia del medio exterior,
que se supone ejerce una presión constante Po, resulta:
neto
W sistema
. cerrado = Q − Δ E − P0 (V 2 − V1 )
y aunque existan modificaciones de volumen durante la transformación, resulta que la suma
de los valores de todos los términos (P0ΔV) se anulan.
Las transformaciones de un sistema cerrado, sin energía potencial o cinética, obedecen
a la ecuación:
Q – W = ΔU
y como ΔU
sistema cerrado
sistema cerrado
representa cualquier forma de energía interna, es perfectamente
válida independientemente de que en la transformación existan reacciones químicas o
nucleares.
El concepto de sistema se refiere únicamente a la sustancia que evoluciona, considerando a
la envoltura que la rodea como parte del medio exterior; sin embargo, en las experiencias de
laboratorio se considera la envoltura (o frontera) como un recipiente que contiene al sistema
y que forma parte de él.
ECUACIONES ENERGÉTICAS DE UN SISTEMA
Partiendo de la función Energía Interna:
U = U (v; T)
efectuamos la diferencial dU
⎛ ∂U ⎞
⎛ ∂U ⎞
dU = ⎜
⎟ dv + ⎜
⎟ dT
⎝ ∂v ⎠ T
⎝ ∂T ⎠ v
XXIII
FISICA II 2010
TEMA IV
JUAN J CORACE
Como u, v y T son todas ellas propiedades, la derivada parcial también es una propiedad, y
a la derivada de U respecto de T a v constante, se denomina calor específico a volumen
constante cV
⎛ ∂U ⎞
cV = ⎜
⎟
⎝ ∂T ⎠ v
Concepto básico:
La energía interna
de un gas es solo
función
de
la
temperatura
La expresión dQ = dU + dW, se puede poner en otra forma recordando que W = P.dv
⎛ ∂U ⎞
⎛ ∂U ⎞
dQ = ⎜
⎟ dT + Pdv O bien
⎟ dv + ⎜
⎝ ∂T ⎠ v
⎝ ∂v ⎠ T
⎡⎛ ∂U ⎞
⎤
⎛ ∂U ⎞
dQ = ⎢⎜
⎟ + P ⎥ dv + ⎜
⎟ dT
⎝ ∂T ⎠ v
⎣⎝ ∂v ⎠ T
⎦
Dando lugar a los siguientes casos particulares:
a) Procesos a v = constante, dv =0 → Q = ΔU
⎛ ∂U ⎞
dQ = ⎜
⎟ dT = cv dT
⎝ ∂T ⎠ v
[4.34]
Donde cV que es la expresión del calor específico a volumen constante, medible por el método
calorimétrico.
b) Procesos a P = constante, dp=0 → Q = ΔΗ
con H= U+PV o (h=u+Pv)
⎛ ∂U ⎞
⎛ ∂U ⎞
dQ = ⎜
⎟ dT
⎟ dv + Pdv + ⎜
⎝ ∂T ⎠V
⎝ ∂v ⎠ T
⎡⎛ ∂U ⎞
⎤
⎡⎛ ∂U ⎞
⎤
dQ = c P dT = ⎢⎜
⎟ + P ⎥ dv + cv dT ⇒ c P dT − cV dT = ⎢⎜
⎟ + p ⎥ dv
⎣⎝ ∂v ⎠ T
⎦
⎣⎝ ∂v ⎠ T
⎦
⎡⎛ ∂U ⎞
⎤⎛ ∂v ⎞
c p −cv = ⎢⎜
⎟ + p ⎥⎜
⎟
⎣⎝ ∂v ⎠ T
⎦⎝ ∂T ⎠ P
[4.35]
que es la ecuación de Mayer generalizada. Para un gas perfecto: cp - cv = R
⎡⎛ ∂U ⎞
⎤ ⎛ ∂v ⎞
⎛ ∂p ⎞ ⎛ ∂ v ⎞
c p −cv = ⎢⎜
⎟
⎟ ⎜
⎟ + p ⎥⎜
⎟ = T⎜
⎝ ∂T ⎠V ⎝ ∂T ⎠ P
⎣⎝ ∂v ⎠T
⎦ ⎝ ∂T ⎠ P
teniendo en cuenta que α es el coeficiente de dilatación volumétrico
1 ⎛ ∂v ⎞
⎛ ∂v ⎞
⎟ = α .v
⎟ ⇒⎜
v ⎝ ∂T ⎠ p
⎝ ∂T ⎠ P
α= ⎜
XXIV
FISICA II 2010
TEMA IV
JUAN J CORACE
se obtiene la ecuación de Mayer en función del coeficiente de dilatación:
⎛ ∂P ⎞
c p −cv = α .T .v⎜ ⎟
⎝ ∂T ⎠ v
c) Procesos a: T = Constante; dT = 0
[4.36]
→ Q = W por ser ΔU = 0
⎡⎛ ∂U ⎞
⎤
⎛ ∂P ⎞
dQ = ⎢⎜
⎟ + P ⎥ dv = T ⎜
⎟ dv
⎝ ∂T ⎠ v
⎣⎝ ∂v ⎠ T
⎦
d)Procesos a: Q = Constante; dQ= 0 → -dW = dU
⎡⎛ ∂U ⎞
⎤⎛ dv ⎞
⎡⎛ ∂U ⎞
⎤
⎛ ∂P ⎞ ⎛ dv ⎞
⎛ ∂U ⎞
0 = ⎢⎜
⎟
⎟ ⎜
⎟ = −T ⎜
⎟ + p ⎥⎜
⎟ + P ⎥ dv + ⎜
⎟ dT ⇒ cv = − ⎢⎜
⎝ ∂T ⎠ v ⎝ dT ⎠ γ
⎝ ∂T ⎠ v
⎣⎝ ∂v ⎠ T
⎦⎝ dT ⎠ γ
⎣⎝ ∂v ⎠ T
⎦
que es la expresión matemática del calor específico a volumen constante en un proceso
adiabático.
PROCESO ADIABATICO
dQ = cV .dT + Pdv = 0 esto equivale a decir -dW = dU
cV .dT = - Pdv = 0
cV dT +
como P =
RT
v
RT
dv = 0
v
cV dT
dv
=−
RT
v
cV dT
dv
.
= − ; Como cV es constante, integramos:
R T
v
cV T2
v
ln = − ln 2
R T1
v1
Esto lo puedo expresar mejor como:
T2 ⎛ v 2
=⎜
T1 ⎜⎝ v1
⎞
⎟⎟
⎠
R
cV
Como R = cP - cV; y a la relación de los calores específicos cP/cV se la denomina γ ,
podemos expresar esta última igualdad así:
T2 ⎛ v 2 ⎞
=⎜ ⎟
T1 ⎜⎝ v1 ⎟⎠
Aplicando el concepto de gas ideal:
XXV
γ −1
FISICA II 2010
TEMA IV
T2 ⎛ P2 ⎞
=⎜ ⎟
T1 ⎜⎝ P1 ⎟⎠
γ −1
JUAN J CORACE
P2 ⎛ v1 ⎞
=⎜ ⎟
P1 ⎜⎝ v 2 ⎟⎠
γ
γ
Generalizamos para un proceso politrópico:
Pvn = constante
El trabajo se calcula: W =
v2
v2
∫ Pdv = P .v ∫ v
1
v1
n
1
−n
dv →
v1
P1 .v1n 1− n
P v − P1v1
W=
(
v 2 − v11− n ) = 2 2
1− n
1− n
Si n es igual a 1, estaremos en un caso isotérmico y la expresión del trabajo será:
v2
v2
v
p
dv
= mRT ln 2 = mRT ln 1
v
v1
p2
v1
W = ∫ Pdv = P ∫
v1
Cada proceso casi en equilibrio de un gas ideal está asociado con un valor particular de “n”:
Si n=1 estamos en el caso de un proceso isotérmico
Si n=∞ estamos en el caso de un proceso isométrico o V=CTE
Si n=0 es el caso de un proceso isobárico o P=CTE
Si n=γ es el caso de un proceso adiabático o sea con cP = CTE
ANALISIS DEL EXPONENTE “n”
Partiendo de la expresión general diferencial del calor: dQ = c dT
E igualando a la de un gas perfecto, por ejemplo dQ = cV dT + Pdv
cdT = cV dT + Pdv ;
(cV
(cV
RT
dv = 0 ;
v
− c )dT +
− c )dT + Pdv = 0
Para un gas perfecto P=RT/v
dT
R dv
+
= 0;
(cv − c ) v
T
R
Tv
cV − c
ln T +
= ln cte
Esta es la expresión de las politrópicas en el plano (v,T).
Partiendo de la ecuación:
XXVI
R
ln v = ln cte ;
(cv − c )
FISICA II 2010
TEMA IV
dQ =
1
(γPdv + vdp );
γ −1
dT =
Pdv + vdP
;
R
c
R
γ −1
c(Pdv + vdP ) =
→
c(Pdv + vdP ) = cv (γPdv + vdp );
Pdv(c −
Pv=RT; Pdv+vdP =RdT
[4.37]
Pdv + vdP
1
(γPdv + vdp );
=
R
γ −1
Como γ=c P /c V
1
(γPdv + vdp );
γ −1
cdT =
cV =
JUAN J CORACE
R
(γPdv + vdp );
γ −1
Pdv(c − γcV ) = vdP(cV − c)
→
queda:
cP
cV ) = vdP(cV − c)
cV
Dividiendo todo por c V – c;
Pdv
n=
Resulta nPdv + vdP = 0 ;
(c
p
(c
p
(c P − c )
+ vdP = 0
(cv − c )
− c)
(cv − c )
p
dP
= −n ;
dv
v
;
y llamando “n” a la relación
[4.38]
con n>0 →dP/dv <0
Concepto básico:
Los valores de cp y
cv de sustancias
incompresibles son
idénticos
y
se
denotan con c
n ln v + ln P = ln cte; pv n = cte
Y al integrar será
Ahora bien n =
Pdv(c P − c) + vdP(cV − c) = 0
→
− c)
(cv − c )
; entonces trabajando la expresión hallamos c =
(γ − n )
(1 − n )
cv
El calor puesto en juego en una transformación politrópica es:
dQ = c dT =
(γ − n ) dT
(1 − n )
dQ =
o bien
(γ − n ) .c dT ;
(1 − n ) V
integramos
cV
Q1− 2 =
(γ − n ) .c (T − T )
(1 − n ) V 2 1
[4.39]
Y el trabajo politrópico de circulación se define en la forma:
v2
P2 2
v1
P1
Wcirc = − ∫ vdP = − γ
∫
⎡⎛ P
n
dP
⎢⎜ 2
=
−
RT
;
resuelta
esta
integral
queda
W
1 ⎜
circ
1/ n
n −1
⎢⎝ P1
p
⎣
⎞
⎟⎟
⎠
n −1
n
⎤
− 1⎥
⎥
⎦
En el caso de una transformación a volumen constante el calor transferido puede ser
obtenido partiendo de la expresión:
XXVII
FISICA II 2010
dQ =
TEMA IV
1
(γPdv + vdp );
γ −1
como v=CTE
JUAN J CORACE
dQ =
1
(vdp );
γ −1
Q=
1
vdP
γ −1 ∫
En el caso de una transformación a presión constante, el trabajo viene dado por
la expresión: W exp = P(v 2 – v 1 ) = R(T 2 – T 1 )
Y el calor disipado viene dado por: dQ = cdT = cV dT + Pdv
Integrando esta expresión entre 1 – 2
Q1− 2 =
γ
γ −1 ∫
Pdv
[4.40]
Y aquí conviene recordar el concepto de entalpía, muy asociado a estos
procesos:
ΔQ a P= cte será;
= ΔQ P =cte = (u 2 − u1 ) + ΔT1− 2 = (u 2 + P2 v 2 ) − (u1 + P1v1 ) = h2 − h1
Entonces en un proceso a presión constante Q= h2 − h1
La entalpía es una función de estado y técnicamente se la puede considerar como la función
termodinámica más importante, por su amplísima utilización en equipos, máquinas y
motores térmicos.
Finalmente si
h= u + Pdv; dh = du +Pdv+vdP = (dQ – P dv) +Pdv + vdP
entonces
h= dQ+ vdP
[4.41]
En los sólidos el término vdP es insignificante por lo que ΔH = ΔU ≅cprom.ΔΤ; para líquido
comúnmente se encuentran dos casos especiales:
a) procesos a presión constante: como en los calentadores, ΔΡ=0, ΔΗ= ΔU ≅cprom.ΔΤ
b) procesos a temperatura constante: como las bombas ΔT=0, ΔH = vdP
para un proceso que ocurre entre dos estado 1-2 esta última relación se puede expresar
como:
h2 − h1 = v( P1 − P2 )
XXVIII
FISICA II 2010
TEMA IV
JUAN J CORACE
APENDICE
CONCEPTOS BASICOS
Una Ley es un enunciado basado en observaciones de múltiples experimentos
El calor latente es la energía que debe ser transferida en forma de calor a una sustancia
mantenida a presión constante para que ocurra un cambio de fase.
El calor de fusión y el de sublimación son insensibles a los cambios de temperatura yo
presión
La energía interna de un gas solo es función de la temperatura.
La entalpía solo es función de T para un gas ideal.
La diferencia entre cp y cv para un gas ideal es siempre constante
Con frecuencia es aceptable tratar a cp y cv como constantes.
Una vez encontrado el valor de cp se puede calcular cv como R – cp
Para líquidos la diferencia entre cp y cv es muy pequeña e ignorada.
La velocidad es aproximadamente uniforme para flujo turbulento en tubos.
Trabajo de flujo es el trabajo debido a la presión necesaria para mover el fluido
Trabajo de eje es el trabajo que resulta de un eje que está girando
PROPIEDADES TÉRMICAS DEL AGUA.
Es interesante estudiar las propiedades térmicas del agua, que se diferencia de la de los
demás líquidos, dada la importancia que tiene el agua para la vida y la ingeniería misma
Esta particularidad que tiene el agua es debida a su estructura. El agua líquida consiste en
moléculas unidas entre sí unidas por puentes de hidrógeno.
Estas uniones son débiles, pero se encuentran en un gran número, lo que muestra que es
necesario un mayor aporte de energía para romperlas. Esto se refleja en el valor de la
energía para producir la vaporización del agua (entalpía de vaporización), que es
característicamente más alto que la de otros líquidos. Por ejemplo, los valores de entalpía
-1
de vaporización a la temperatura de ebullición normal, para el agua son de 540 cal g , y
-1
para el etanol es de 204 cal g . La entalpía de vaporización está relacionada con la energía
necesaria para producir un cambio de fase (líquido a vapor). Para el caso del agua, es
entonces necesaria una mayor cantidad de energía para vaporizar el agua que el que
necesitaría el etanol.
Supongamos que una persona de 60 kg ingiere 2500 kcal diarias. Si esta energía fuera
transformada completamente en calor, las consecuencias sobre esa persona serían
XXIX
FISICA II 2010
TEMA IV
JUAN J CORACE
altamente indeseables. Si la persona constituyera un sistema adiabático, no podría perder
ese calor hacia el ambiente, y la temperatura del cuerpo aumentaría. Considerando que el
cuerpo humano está constituido en un 80% de agua, el aumento de temperatura sería:
ΔT =
ΔH
2.5 x10 6 cal
=
= 52 º C
C P (1cal .g −1 º C −1 )(0.8 x 60 x10 3 g )
lo cual, obviamente provocará la muerte de la persona por el solo hecho de comer
normalmente. Todos sabemos que esto no es lo que sucede, y el calor generado puede
eliminarse porque nuestro cuerpo no se comporta como un sistema adiabático. El calor
generado se utiliza entonces para vaporizar el agua a la temperatura corporal. Por lo tanto a
37°C, la entalpía de vaporización del agua es de 574 cal g-1, y la cantidad de agua que se
evaporaría resulta ser:
m=
QP
2.5 x10 6 cal
=
= 4400 g ≈ 4,4 L
ΔH VAP (574cal .g −1 )
Por lo tanto, el cuerpo debiera transpirar 4.4 L de agua si toda la energía aportada por la
ingesta fuera transformada en calor, de manera de mantener la temperatura corporal
constante. Nótese que el ejemplo analizado se trata de una situación límite, pues la energía
obtenida por la ingesta es utilizada también para realizar trabajo. Aunque no es ajeno a
todos el hecho que cuando ingerimos alimentos con alto contenido energético, nuestro
cuerpo transpira, como mecanismo homeotérmico.
El valor de la capacidad calorífica del agua también cumple un papel muy importante a la
hora de explicar las ventajas del agua como sustento de la vida. Nuevamente comparado
-1
-1
con el etanol, los calores específicos valen 1 y 0.6 cal g °C para el agua y para el etanol,
respectivamente. Esto quiere decir que, para una misma cantidad de calor absorbido, el
aumento de la temperatura será menor para el agua que para otros líquidos. El valor para
los calores específicos da cuenta de la capacidad que tiene el agua para disipar el calor
absorbido, lo que lo convierte en un excelente refrigerante
BIBLIOGRAFIA PARA ESTA UNIDAD
CENGEL y BOLES – TERMODINAMICA 5TA EDICIÓN. EDITORIAL MC GRAW HILL, 2003
FERMI, ENRICO.- TERMODINÁMICA. EUDEBA. 1973.
HECHT EUGENE – FISICA EN PERSPECTIVA. EDITORIAL PEARSON, 1999
HUANG, FRANCIS – INGENIERIA TERMODINAMICA. EDITORIAL CECSA, 2006
POTTER Y SCOTT – TERMODINAMICA, EDITORIAL THOMPSON, 2004
ROLLE, KURT – TERMODINAMICA. EDITORIAL PEARSON. 6TA EDICION 2006
TORREGROSA HUGUET – INGENIERIA TERMICA. EDIT. ALFAOMEGA.-UNIV.DE VALENCIA, 2004
A
WARK, K. (H);RICHARDS, D – TERMODINÁMICA 6 EDICIÓN. EDITORIAL MCGRAW-HILL, 2001.
XXX