Calcular los parámetros y los vértices de las siguientes hipérbola

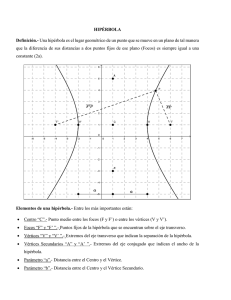
Problema realizado por Elena Abad Felip
Enunciado:
Calcular los parámetros y los vértices de las siguientes hipérbola equilátera:
xy = 16
a) Según sus asíntotas
b) Según sus ejes
Bases teóricas:
•
La hipérbola equilátera es aquella cuyos ejes son iguales a = b
•
La ecuación de las asíntotas (rectas que cortan a la función en el infinito)
b
de una hipérbola es: y = ± x
a
•
La ecuación de la hipérbola equilátera referida a sus asíntotas (asíntotas
a2
como ejes de coordenadas) si el giro es de 45º es: x ⋅ y =
2
•
La ecuación reducida de la hipérbola equilátera es: x 2 − y 2 = a 2
•
En una hipérbola siempre se cumple que c 2 = a 2 + b 2
•
En una hipérbola equilátera la excentricidad siempre es: e = 2 ⇒ e =
•
Teorema de Pitágoras para averiguar coordenadas: d 2 = x 2 + y 2 (“d” es
la distancia al punto, “x” coordenada “x”, “y” coordenada”y”)
•
Elementos o parámetros de una hipérbola:
c
a
− ejes focal e imaginario: (rectas que contienen los focos y los vértices)
− centro: (intersección de los ejes)
− focos: F, F’(puntos fijos)
− vértices: A, A’, B, B’(intersecciones de la hipérbola con los ejes)
− semiejes mayor y menor: “a”, (la mitad de la longitud del segmento AA’),
“b”(la mitad de la longitud del segmento BB’)
− semidistancia focal: “c”, (la mitad de la longitud del segmento CC’)
Resolución gráfica:
a) Según sus asíntotas
•
Se dibujan las asíntotas que van a ser los ejes de coordenadas.
• Se representan los focos (F y F’) con las coordenadas que les
corresponden y que al ser la hipérbola equilátera son (±x, ± x) en
este caso x = 32
• Se representan los vértices (A, A’, B y B’) también con sus
respectivas coordenadas que también son iguales (±x, ±x) y que en
este caso son x = 4
• Se trazan los ejes de la hipérbola (real e imaginario) que pasarán
por los vértices y los focos y son bisectrices de los ejes de
coordenadas por ser la hipérbola equilátera.
• Se dibuja la hipérbola sabiendo que es el lugar geométrico de los
puntos cuya diferencia de distancias a los focos es constante.
b) Según sus ejes
• Se dibujan los ejes de coordenadas, que coinciden con los ejes
de la hipérbola el eje real con el eje x y el imaginario con el eje y
• Se representan los focos con las coordenadas que les
corresponden. Al encontrarse los focos en el eje real (eje x) serían
(±x, 0) en este caso x = 8
• Se representan los vértices. El A y el A’ se encuentran en el eje
real (eje x) serán (±x, 0) y los vértices B y B’ que se encuentran en el
eje imaginario (eje ±y) serán (0, y) Además, como es una hipérbola
equilátera, x = y. En este caso concreto x = 32
• Se dibujan las asíntotas que son bisectrices de los ejes de
coordenadas por ser hipérbola equilátera.
• Se dibuja la hipérbola sabiendo que es el lugar geométrico de los
puntos cuya diferencia de distancias a los focos es constante.
Cálculos:
a) Según sus asíntotas
Centro de la hipérbola (0, 0)
Los ejes de coordenadas son las asíntotas
Los ejes real e imaginario son bisectrices de los ejes de coordenadas.
1. Se compara la ecuación que tenemos con la ecuación de una hipérbola
referida a sus asíntotas y se encuentra “a”(distancia del centro de la
hipérbola a los vértices A y A’)
xy = 16


a2
xy
=

2

a2
= 16
2
a 2 = 32
a = 32 = 4 2
2. Teniendo en cuenta que en una hipérbola equilátera “a = b” (semiejes
iguales) se utiliza la ecuación de las constantes de la hipérbola y el valor
de “a” que hemos encontrado y descubrimos “c”(semidistancia focal)
c 2 = a 2 + b 2

a = b
a 2 = 32

c2 = a 2 + a 2
c 2 = 32 + 32
c 2 = 64
c=8
3. Los ejes de la hipérbola equilátera referida a sus asíntotas no coinciden
con los ejes de coordenadas sino que son sus bisectrices. Para hallar la
posición de los vértices (que están colocados en los ejes de la hipérbola),
se deben averiguar sus coordenadas (“x1”e “y1”). Tenemos la distancia del
centro a los vértices (“a”=”b”, semiejes) y las coordenadas son iguales al
ser el eje bisectriz. Se utiliza Pitágoras:
2
a 2 = x1 + x1
d 2 = x 2 + y 2
 2
2
d = a = 32
x = y
1
 1
32 = 2x 1
2
2
2
x 1 = 16
x 1 = ±4
4. Para hallar las coordenadas de los focos (“x2”, “y2”) se utiliza Pitágoras y
todo lo de antes cambiando “a” por “c”(semidistancia focal):
2
c2 = x 2 + x 2
d = x + y
 2
2
d = c = 64
x = y
2
 2
2
2
2
64 = 2x 2
2
2
2
x 2 = 32
x 2 = ± 32 = ±4 2
5. Ya con todos los datos calculados se escriben los parámetros y vértices
según sus asíntotas:
Eje real: y = x
Ejes de la hipérbola
Eje imaginario:
y = 0
Asíntotas 
x = 0
Vértices
A(4,4)
A' (−4,−4)


B(−4,4)
B' (4,−4)
F(4 2 ,4 2 )
Focos 
F' (−4 2 ,−4 2 )
y = −x
e=
Excentricidad
c
a
e=
8
e= 2
4 2
b)Según sus ejes
Centro de la hipérbola (0, 0)
Los ejes de coordenadas son los ejes real e imaginario de la hipérbola.
Las asíntotas son bisectrices de los ejes de coordenadas.
1. Se quiere saber la ecuación de esta hipérbola equilátera y ya se ha
calculado “a” antes así que se sustituye en la ecuación general:
x 2 − y 2 = a 2
 2
a = 32
x 2 − y 2 = 32
2. Los datos son los mismos que se han calculado antes pero colocados de
distinta forma. En este caso no hace falta Pitágoras por que los ejes de la
hipérbola están colocados de forma que coinciden con los ejes de
coordenadas y las distancias irán sobre el eje x o y, solo tendrán una
componente.
Eje real: y = 0
Ejes de la hipérbola
Eje imaginario:
y = x
Asíntotas 
y = − x
A(4 2 ,0)

A' (−4 2 ,0)
Vértices 
B(0,4 2 )

B' (0,−4 2 )
F(8,0)
Focos 
F' (−8,0)
Excentricidad ⇒ e = 2
x=0