IMAGINARIO EJE REAL F1 b a ASÍNTO TA A c EJE B F2 N M P

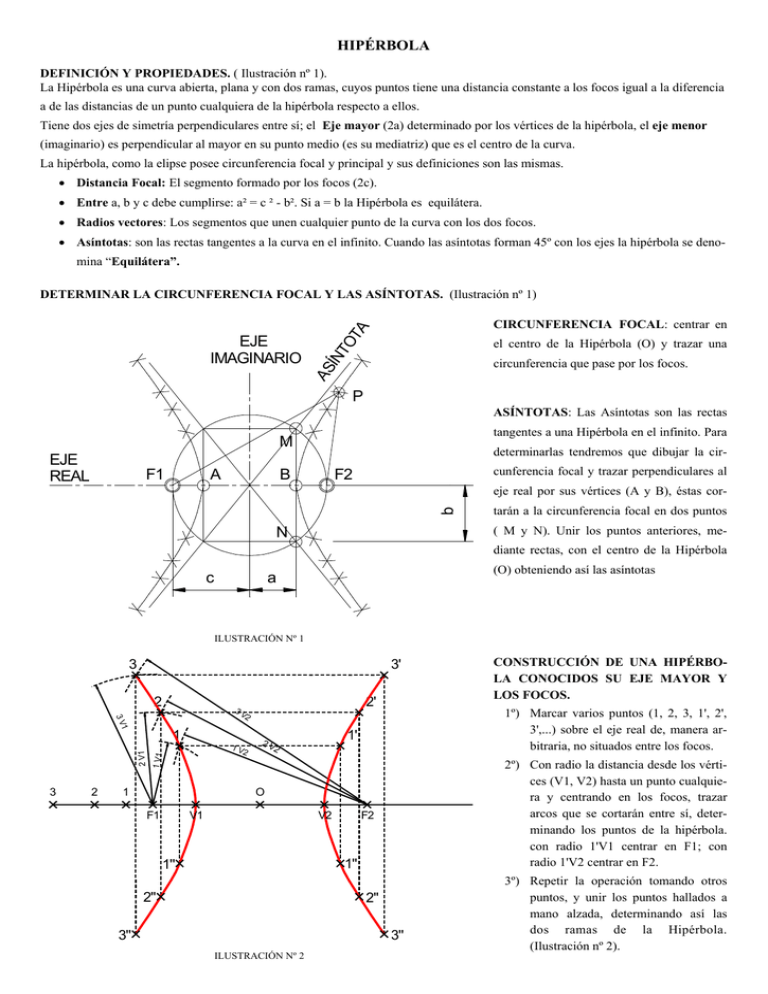
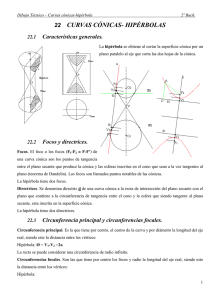
HIPÉRBOLA
DEFINICIÓN Y PROPIEDADES. ( Ilustración nº 1).
La Hipérbola es una curva abierta, plana y con dos ramas, cuyos puntos tiene una distancia constante a los focos igual a la diferencia
a de las distancias de un punto cualquiera de la hipérbola respecto a ellos.
Tiene dos ejes de simetría perpendiculares entre sí; el Eje mayor (2a) determinado por los vértices de la hipérbola, el eje menor
(imaginario) es perpendicular al mayor en su punto medio (es su mediatriz) que es el centro de la curva.
La hipérbola, como la elipse posee circunferencia focal y principal y sus definiciones son las mismas.
 Distancia Focal: El segmento formado por los focos (2c).
 Entre a, b y c debe cumplirse: a² = c ² - b². Si a = b la Hipérbola es equilátera.
 Radios vectores: Los segmentos que unen cualquier punto de la curva con los dos focos.
 Asíntotas: son las rectas tangentes a la curva en el infinito. Cuando las asíntotas forman 45º con los ejes la hipérbola se denomina “Equilátera”.
DETERMINAR LA CIRCUNFERENCIA FOCAL Y LAS ASÍNTOTAS. (Ilustración nº 1)
AS
ÍN
TO
TA
EJE
IMAGINARIO
CIRCUNFERENCIA FOCAL: centrar en
el centro de la Hipérbola (O) y trazar una
circunferencia que pase por los focos.
P
ASÍNTOTAS: Las Asíntotas son las rectas
tangentes a una Hipérbola en el infinito. Para
M
EJE
REAL
F1
A
determinarlas tendremos que dibujar la cir-
B
cunferencia focal y trazar perpendiculares al
F2
b
eje real por sus vértices (A y B), éstas cor-
N
tarán a la circunferencia focal en dos puntos
( M y N). Unir los puntos anteriores, mediante rectas, con el centro de la Hipérbola
c
(O) obteniendo así las asíntotas
a
ILUSTRACIÓN Nº 1
3
3'
2
1
3V
1
2
1V
2
1 V1
2 V1
3
2'
3V
2
1
1º) Marcar varios puntos (1, 2, 3, 1', 2',
3',...) sobre el eje real de, manera arbitraria, no situados entre los focos.
1'
2V
2
2º) Con radio la distancia desde los vértices (V1, V2) hasta un punto cualquiera y centrando en los focos, trazar
arcos que se cortarán entre sí, determinando los puntos de la hipérbola.
con radio 1'V1 centrar en F1; con
radio 1'V2 centrar en F2.
O
F1
V1
V2
F2
1''
1''
2''
2''
3''
3''
ILUSTRACIÓN Nº 2
CONSTRUCCIÓN DE UNA HIPÉRBOLA CONOCIDOS SU EJE MAYOR Y
LOS FOCOS.
3º) Repetir la operación tomando otros
puntos, y unir los puntos hallados a
mano alzada, determinando así las
dos ramas de la Hipérbola.
(Ilustración nº 2).