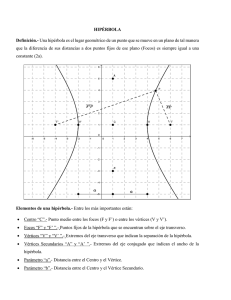
LA HIPERBOLA Integrante: Andrea Acuña Curso: 10c ITICSA 2018 Hipérbola Una hipérbola es una curva abierta de dos ramas obtenida cortando un cono recto mediante un plano no necesariamente paralelo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución. En geometría analítica, una hipérbola es el lugar geométrico de los puntos de un plano, tales que el valor absoluto de la diferencia de sus distancia a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva ELEMENTOS DE LA HIPERBOLA *Focos: son los dos puntos fijos (F1yF2). *Radio vector: es la distancia R de un punto de la hipérbola (P) a cualquiera de los focos. *Eje no transverso: es la mediatriz T del eje focal. *Centro: es el punto medio O de los dos focos. También se puede definir como la intersección del eje focal y el transverso. *Vértices: son los dos puntos de intersección del eje foca con la hipérbola (V1yV2). *Distancia focal: es la distancia2centre focos. También se denota comoF1F2. *Eje real: es la distancia2aentre vértices. *Eje imaginario: es la distancia2bde los puntosB1yB2. Los puntos B1y B2se generan como vemos en las relaciones entre semiejes. Así pues, existe una relación entre los semiejes y la distancia focal: *Asíntotas: son las líneas rectas (A1yA2) que se aproximan a la hipérbola en el infinito. *Puntos interiores y exteriores: la hipérbola divide el plano en tres regiones. Dos regiones que contienen un foco cada una y otra región sin ningún foco. Los puntos contenidos en las regiones con un foco se llaman interiores (I) y los otros exteriores (Ex). Ecuación de la hipérbola La ecuación de la hipérbola se puede expresar cuando su centro es O=(o1,o2) como: Si la hipérbola tiene su centro en el origen, O=(0,0), su ecuaciones: Además, los puntos de una hipérbola son los que cumplen la ecuación general de la hipérbola: Siendo A,B,C,DyE escalares (números reales) y necesariamente debe cumplir que los coeficientes de X2 e Y2 (A y C) son no nulos y tienen diferente signo. Excentricidad Secciones cónicas. La excentricidad e de una hipérbola es un valor definido como: e=c/a donde: c representa la mitad de la distancia del eje focal. a representa la mitad de la distancia del eje mayor. Ya que c es un valor mayor que a , la excentricidad de una hipérbola es siempre mayor que 1. Hipérbola en la vida cotidiana las estructuras hiperboloide son estructuras designadas con geometría hiperbólica. A menudo se trata de estructuras altas como torres donde se aprovecha la resistencia estructural de la geometría hiperbólica para apoyar un objeto. Las primeras estructuras hiperboloides fueron construidas por el ingeniero ruso Vladimir Shujov