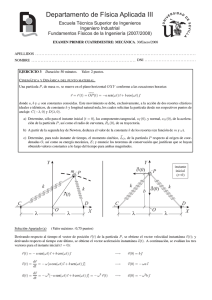
MEC´ANICA CU´ANTICA II. Duración: cuatro horas 1. Como se vio

MECÁNICA CUÁNTICA II.
Duración: cuatro horas
1. Como se vio en clase, el grupo de Poincaré, x → Λx+a, se puede representar en L2 (R4 ),
con generadores
P µ = i∂ µ ,
J µν = xµ P ν − xν P µ .
El grupo conforme (dimensión 15) se completa añadiendo las siguientes transformaciones:
xµ + bµ x2
µ
s µ
µ
x 7→ e x ,
x 7→
,
1 + 2bν xν + b2 x2
con coordenadas s y bµ (x2 = xµ xµ , ı́dem b2 ). Se pide:
a) Calcular los generadores asociados a las nuevas transformaciones (D y C µ ). Usar
el convenio δL = −δaµ P µ + 12 δωµν J µν + δsD + δbµ C µ .
b) Calcular los conmutadores [P µ , D] y [P µ , C ν ] y expresarlos como combinación lineal
de P , J, D, y C.
2. En clase, partiendo del operador hamiltoniano, se construyó la integral de caminos para
una partı́cula de masa M en un potencial V (x, t). Se pide:
a) Hacer la construcción análoga para un partı́cula con carga q en un campo electromagnético con potenciales A(x, t) y Φ(x, t). Se puede suponer que A satisface la
condición de gauge de Coulomb,
∇A = 0, y q = ~ = c = 1. Se puede usar la
hx|O|pi
hx|eǫO |pi
= exp ǫ
+ O(ǫ2 ), para un operador genérico O.
identidad
hx|pi
hx|pi
b) En ausencia de potencial vector, la inserción de un operador f (p̂) en tiempo tj
daba lugar a un factor
xj+1 − xj
,
(1)
hf (M vj + q)iq ,
vj :=
ǫ
en la integral de caminos. Estudiar la modificación que introduce A en este factor.
3. En una teorı́a bosónica, sea A un operador tipo campo (combinación lineal de operadores
de creación y destrucción).
a) El valor esperado h0|eA |0i se puede expresar como una función de la contracción
AA. Encontrar dicha expresión. Se puede usar el teorema de Wick, o bien CampbellHausdorff con A = A(+) + A(−) , relacionando [A(+) , A(−) ] con AA.
b) Usando el resultado anterior encontrar la distribución de probabilidad de φ en el
vacı́o, siendo φ = fα∗ aα + fα a†α (los fα son coeficientes numéricos). Notar que la
densidad pedida seR puede escribir como ρ(x) = h0|δ(φ − x)|0i. Sugerencia: usar la
identidad δ(x) = eikx dk/2π.
4. Calcular
Z
dξ3 dξ2 dξ1 exp(a·ξ b·ξ c·ξ), donde a, b y c son tres vectores arbitrarios en
R3 y ξ son tres generadores del álgebra de Grassmann.
Puntuación de estos ejercicios: (1,5 + 1,5) + (1,5 + 1,5) + (1,5 + 1,5) + 1.