página 112

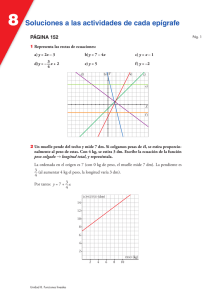
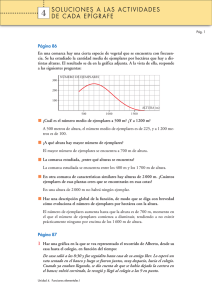
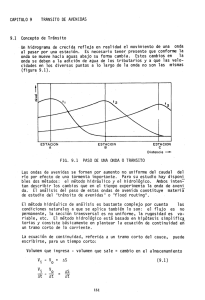
5
Soluciones a “Ejercicios y problemas”
PÁGINA 112
Pág. 1
■ Practica
Funciones lineales
1
Asocia a cada función su ecuación. Di, en cada caso, cuál es su pendiente.
a) y + 2 = 0
b) 3x – y = 3
c) y = 2 – x
d) 2x – 3y = 12
2
–2
Y
b) 3x – y = 3
d) 2x – 3y = 12
a) m = 0
2
–2
4
6
X
a) y + 2 = 0
–4
c) y = 2 – x
2
Pendientes:
b) m = 3
c) m = –1
d) m = 2/3
Representa las siguientes funciones lineales:
y = 2x – 3
Y
a) y = 2x – 3
4
y=—x
7
y = 2,5
b) y = 4 x
7
c) y = –3x + 10
5
2
X
d) y = 2,5
3x + 10
y = – ————
5
3
4
Resuelto en el libro de texto.
Halla, en cada caso, la ecuación de las rectas que pasan por los puntos A y B.
a) A(3, 0), B(5, 0)
b) A(–2, –4), B (2, –3)
c) A(0, –3), B(3, 0)
d) A(0, –5), B(–3, 1)
a) y = 0
b) m = –3 + 4 = 1 ; y + 4 = 1 (x + 2) 8 y = 1 x – 7
2+2
4
4
4
2
c) m = 3 = 1; y + 3 = x 8 y = x – 3
3
d) m = 1 + 5 = –2; y + 5 = –2x 8 y = –2x – 5
–3
Funciones definidas a trozos
5
¿A cuál de las siguientes funciones corresponde la gráfica dibujada?
°2x + 5
§
f (x) = ¢x + 5
§2x
£
si –3 Ì x Ì –1
si 0 Ì x < 3
si 3 Ì x Ì 8
Unidad 5. Funciones elementales
°2x + 5
§
g(x) = ¢5 – x
§2
£
si –3 Ì x < 0
si 0 Ì x < 3
si 3 Ì x Ì 8
5
Soluciones a “Ejercicios y problemas”
si –3 < x < 0
si 0 < x < 3
si 3 < x < 8
°2
§
h (x) = ¢–1
§0
£
Pág. 2
Y
4
2
Una de las otras dos funciones describe la pendiente de esta gráfica en cada punto. ¿Cuál es?
–2
2
4
6
X
La gráfica corresponde a la función g(x).
La función que describe la pendiente de la gráfica en cada punto es h(x).
6
Representa las siguientes funciones definidas a trozos:
si x Ì –1
°2x
°–x + 3
si x < 0
°–3
§
§
a) y = ¢–2
c)y = ¢2
si –1 < x Ì 3 b) y = ¢
§x – 5 si x > 3
§x
£2x + 1 si x Ó 0
£
£
a)
b)
c)
Y
Y
2
Y
X
2
X
2
7
Escribe la ecuación de la función que corresponde a esta gráfica:
Y
4
2
–8
–6
–4
–2
2
4
• El primer tramo pasa por (–6, 0) y (–4, 4):
m = 4 = 2; y = 2(x + 6) = 2x + 12
–4 + 6
• El segundo tramo pasa por (–4, 4) y (1, 5):
m = 5 – 4 = 1 ; y – 4 = 1 (x + 4) 8 y = 1 x + 24
1+4 5
5
5
5
• El tercer tramo pasa por (1, 5) y (8, 2):
m = 2 – 5 = – 3 ; y – 5 = – 3 (x – 1) 8 y = – 3 x + 38
8–1
7
7
7
7
°2x + 12
si x < – 4
§
24
§1
si – 4 Ì x Ì 1
f (x) = ¢ 5 x + 5
§ 3
§– x + 38 si x > 1
7
£ 7
Unidad 5. Funciones elementales
si x < 1
si 1 Ì x < 2
si x Ó 2
6
8
X
X