Funciones Parte 2 - Web del Profesor

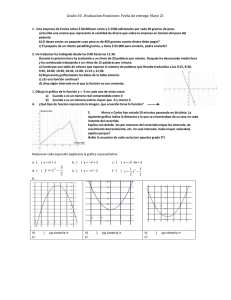
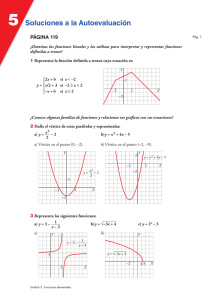
Universidad de Los Andes
Facultad de Ingeniería
Escuela Básica de Ingeniería
Departamento de Cálculo
Funciones Parte 2
Prof. Derwis Rivas Olivo
1. Sea f (x) = (2x2 + 3x − 2)(x − k). Si f (1) = 18, halla el valor de k y calcula los ceros e
intervalos de positividad y de negatividad de f (x).
2. Hallar la expresión y los intervalos de positividad y de negatividad de la función polinómica
f (x) de grado 3 que corta al eje x en (−1, 0), (−5, 0), (1, 0) y en la cual f (0) = 2.
3. Hallar los ceros de la función polinómica f (x) = x2 (x2 − 4)(x + 1) y determinar los intervalos
de positividad y negatividad.
4. Hallar el conjunto de positividad de la función f (x) = (x − 1)(x2 + x − 6).
5. Sea f (x) la función polinómica de grado 3 cuyo gráfico corta al eje x en −4, 2 y 3 y pasa
por el punto (−1, 4). Hallar f (x) y determina los intervalos de positividad y negatividad de
f (x).
6. Calcular los intervalos de positividad y negatividad de f (x) = (x2 + x)(1 − 2x).
7. Hallar el número real k tal que f (x) = x3 + 2x2 − x + k tenga un cero en x = −1 y para el
valor de k hallado, determinar los restantes ceros de f (x).
8. Indicar intervalos de positividad y negatividad de f (x) = (x2 + 5x − 14)(x − 5).
9. Dada la función polinómica f (x) = 2x3 + 2x2 − 4x, hallar los intervalos de positividad y
negatividad.
10. Determinar el conjunto de negatividad de la función f (x) = x3 − 4x2 − 12x.
11. En cada caso defina una función a partir de la cónica dada
1) 4x2 + 16x + 4y 2 − 8y = 0
2) x2 + 2x + 4y 2 − 8y = 0
5) 4x2 − 16x + y 2 − 8y + 32 = 0
6) x2 − 4x + y − 8 = 0
3) 4x2 − 16x + y 2 − 8y + 6 = 0
7) 4x2 − 16x − 9y 2 + 18y + 7 = 0
4) 4x2 − 16x − y 2 − 8y − 2 = 0
8) 4y 2 + 24y − 9x2 + 18x − 9 = 0
12. Encuentra el dominio natural de cada una de las siguientes funciones
r
x+3
2x − 3
2
1) f (x) = x + 4x − 3
2) g(x) =
3) h(x) = 2
x−1
x − 6x + 5
p
x2 + 5x − 3
4) m(x) = |x + 2| + 3
5) n(x) = 5x + 10
6) o(x) =
|3x − 2| − 5
p
p
x+3
7) p(x) = 4 − x2
8) q(x) = 8 − 6x − x2
9) r(x) = 3
x − 4x2 − 5x
13. En cada caso usa la gráfica de la función para determinar el dominio natural. ¿Cuál es el
rango de la función?.
p
1) f (x) = − x2 + 9
2) g(x) = 2x2 + 8x + 7
1p 2
1p 2
3) h(x) =
9x − 18x − 27
4) i(x) = −
9x − 18x − 27
2
2
p
p
1
1
5) j(x) =
3 + 2x − x2
6) k(x) = −
3 + 2x − x2
2
2
1p
1p
7) l(x) =
3 + 2x − x2 − 2
8) m(x) = −
3 + 2x − x2 + 2
2
2
p
1p
9) n(x) = −
3 + 2x − x2 − 2
10) o(x) = x2 − 2x + 2
2
p
p
11) p(x) = − x2 − 2x + 2 + 1
12) q(x) = − x2 − 2x + 2
p
p
13) r(x) = x2 − 2x + 2 − 1
14) s(x) = x2 − 2x + 2 + 1
15) t(x) = x2 − 6x + 11
17) v(x) = 4x + 8
16) u(x) = −x2 + 4x − 2
18) w(x) = 6 − 2x
12 − 10x
20) u(x) =
2
19) F (x) = x − 5
14. Identifica y realiza un bosquejo de las gráficas de las siguientes funciones. Indica, en cada
caso, dominio y rango de la función.
1) f (x) = −2
2) g(x) = −2x + 5
4) m(x) = −3x
1
7) p(x) = 3
x
6) o(x) = x3
5) n(x) = −x
2
8) q(x) = 2
x
9) r(x) =
15. Realice un bosquejo del gráfico de las siguientes funciones
x
3
x
1) y = 2
2) y =
3) y =
2
5) y = log2 (x)
8) y = log1/2 (x)
3) h(x) = 5x
2
6) y = ln(x)
ex
4
x2 + 2
4) y = log1/4 (x)
7) y = log(x)
16. Determina el valor de los siguientes logaritmos (sin calculadora).
1
1
1) log2
2) log1/2
3) log1/3 (27)
64
32
√
1
5) log3
6) log2 2
7) log√2 (4)
81
4) log1000 (0, 1)
√
4
8) log√3 ( 27)
17. Encuentra el valor de las siguientes expresiones
1) 2log2 (5)
2) 95 log3 (5)
3)
e
ln(4)
3
4)
e 3 ln(5)+2 ln(3)
5) 81/2 log2 (5)−3 log2 (3)
18. Resuelve las siguientes ecuaciones
1) log4 (x2 − 6x) = 2
4) log(x) + log(2x − 8) = 1
7) log2 (x − 4) + log2 (x − 3) = 1
10) log2 (x) − log2 (x − 2) = 3
2) 24x 4x−3 = 64x−1
3) 4x+1 = (1/2)2x
√
x+1
3
6) ( 265) 2x−1 = 25
9) ln(x + 3) = 0
2
5) 5x −x = 25
8) − 3 ln(x) = 4
11) log3 |x + 2| = 2
12) 4log2 (x) = 16
19. Sabiendo que log 2 = 0.3010, log 3 = 0.4771, log 5 = 0.6989 encuentra el valor de los siguientes
logaritmos
√
27
1) log(45)
2) log( 210)
3) log √
4) log(360)
3
4
20. Exprese cada uno de los siguientes como un único logaritmo
1) 3 log(x + 1) + 1/3 log 4x + 7
2) 1/2 log2 (x + 2) − 3 log2 (x2 + 1) − 3 log2 (x + 1)
3) 1/3 log3 (x + 2) + 2/3 log3 (x2 − 2) − 1/3 log3 (x − 1) − 5/3 log(x2 − 1)
4) 3 ln(a + 1) − 3 ln(b + 1) + 6 ln(a + b)
21. Realiza un bosquejo del gráfico de las siguientes funciones. Determina, en cada caso, el
dominio y rango e indica los cortes con los ejes coordenados.


si x ≤ 0
 cos(x),
 cosh(x), si x < 0
x,
si 0 < x < 2
sen(x),
si 0 ≤ x ≤ 2π
1) f (x) =
2) g(x) =


−1/2(x − 2), si x > 2
tan(x), si x > 2π


 cosh(x), si x < 0
 sen(x), si x ≤ 0
x + 1,
si 0 < x < 2
sec(x), si 0 < x < 3π/2
3) h(x) =
4) F (x) =


−x + 2, si x ≥ 2
sen(x), si x ≥ 3π/2


 csc(x), si x ≤ −π/2
 |x + 2|, si −4 ≤ x ≤ 0
sec(x), si −π/2 < x < π/2
csc(x), si 0 < x < 2π
5) G(x) =
6) H(x) =


csc(x), si x ≥ π/2
x − 2π, si x ≥ 2π

1
si x ≤ 0
 −2x,
si x < 0
x2 ,
log1/2 (x), si 0 < x ≤ 1
7) L(x) =
8) M (x) =
sech(x), si x > 0

x + 1,
si x > 1

 √
3
si x ≤ 0
 |3x + 9|, si x < 0
 x,
2 − x, si 0 < x < 2
log2 (x), si 0 < x ≤ 4
9) R(x) =
10) T (x) =


8 − 2x,
si x > 4
x − 3, si x ≤ 3
11) s(x) = |4x − 2|
12) t(x) = |3x + 6|
22. Determina el valor numérico de las siguientes expresiones trigonométricas.
sen(1200 ) + sen(2700 )
1 + cos(1350 )
tan(7π/4) + sen(2π/3)
(b)
cos(5π/6) + sen(3π/2)
(a)
(c)
sen2 (2250 ) + cos2 (1350 )
1 + tan(π/3)
23. Resuelve cada una de las siguientes ecuaciones trigonométricas, encontrado todas las soluciones en el intervalo [0, 2π).
√
1) 2 cos(x) + 3 = 0
2) tan2 (x) = 1
3) 2sen2 (x) = 1 + cos(x)
4) tan2 (x) − 3 tan(x) + 1 = 0
5) 4sen2 (x) − 3 = 0
6) 2sen(x) + 1 = 0
7) (sen(x) − 1)(tan(x) + 1) = 0
8) sec2 (x) = 1 + tan(x)
9) cos(2x) = 3sen(x)
√
10) tan(x) = − 3