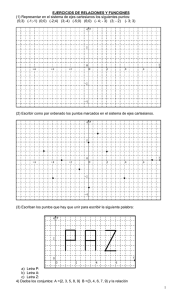
FUNCIÓN-FUNCIÓN DEFINIDA A INTERVALOS 1

FUNCIÓN-FUNCIÓN DEFINIDA A INTERVALOS
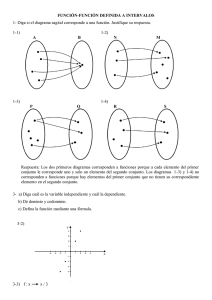
1- Diga si el diagrama sagital corresponde a una función. Justifique su respuesta.
1-1)
1-2)
A
B
1-3)
N
M
1-4)
P
Q
R
S
Respuesta: Los dos primeros diagramas corresponden a funciones porque a cada elemento del primer
conjunto le corresponde uno y solo un elemento del segundo conjunto. Los diagramas 1-3) y 1-4) no
corresponden a funciones porque hay elementos del primer conjunto que no tienen su correspondiente
elemento en el segundo conjunto.
3- a) Diga cuál es la variable independiente y cuál la dependiente.
b) Dé dominio y codominio.
c) Defina la función mediante una fórmula.
3-2)
3-3) f : x
x/3
3-6)
A
B
Respuesta: 3-2) a) variable independiente: x. Variable dependiente: y
b) dominio = {-2, -1, 0, 1, 2} codominio = {-4, -2, 0, 2, 4}
c) y = 2x
3-3) a) variable independiente: x. Variable dependiente: y
b) dominio = R codominio = R
c) y = x / 3
3-6) a) variable independiente: x. Variable dependiente: y
b) dominio = {1, 3, 4, 5, 9} codominio = {1, 2, , , 3}
c) y =
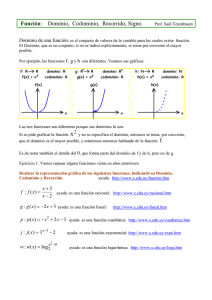
7- Observe el climograma y complete según corresponda (Climograma es la representación gráfica de
los promedios mensuales de las temperaturas y de las lluvias).
Mes
7-1) La mayor temperatura promedio se registró en el mes de …ENERO………………….
7-2) En el mes de marzo la temperatura promedio fue …20ºC………………………….
7-3) La menor temperatura promedio se registró en el mes de …JUNIO Y JULIO………………….
7-4) El mes más lluvioso fue ………ENERO……………………………………………….
7-5) Los meses que tienen el mismo registro de lluvia son …ABRIL Y OCTUBRE – MAYO, JULIO,
AGOSTO Y SETIEMBRE.
9- Dada f (x) = – x + 3 x 2 calcule:
9-1) f (– 1)
9-6) f (r – 1)
9-8) f (a) – f (a + h)
Respuesta: 9-1) f (– 1) = -(-1) + 3(-1)2
=4
9-6) f (r – 1) = -(r-1) + 3(r-1)2
= -r + 1 + 3r2 – 6r +3
= 3r2 – 7r +4
9-8) f (a) – f (a + h) = -a + 3a2 – [-(a+h) + 3(a+h)2]
= -a + 3a2 + a + h – 3a2 – 6ah – 3h2
= h – 6ah – 3h2
9-10) f (2 x) + f (x) = -2x + 3(2x)2 + (-x) + 3x2
= -2x +3(4x2) – x + 3x2
= 15x2 – 3x
11- Diga si la gráfica representa una función. Justifique su respuesta.
11-1)
11-3)
11-2)
11-4)
11-5)
11-6)
Respuesta: Las gráficas correspondientes a los apartados 11-1), 11-4) y 11-5) representan funciones
porque toda recta paralela al eje de las y intersecta a las mismas en no más de un punto.
12- Grafique la función definida a intervalos. Dé dominio y codominio.
12-2)
− 2
g (x) = 
 2x
si 0 ≤ x ≤ 1
si 1 < x < 3
Dom g = [0,3)
12-3)
 x + 1 si
h (x) = 
 x − 3 si
Dom h = [2,7]
Codom g = {-2} U (2,6)
2≤ x<4
4≤x≤7
Codom h = [1,5)
17- Analice si la función es par, impar o ninguna de las dos:
17-1) f (x) = x 2 + 5
17-4) f (x) = 3 x 2 – 2 x
Respuesta: 17-1) f (x) = x 2 + 5
f (-x) = (-x) 2 + 5
=x2+5
= f (x)
17-4) f (x) = 3 x 2 – 2 x
por lo tanto la función f es par
f (-x) = 3(-x) 2 – 2(-x)
=3x2+2x
≠ f (x)
por lo tanto la función f no es par
≠ - f (-x)
por lo tanto la función f no es impar
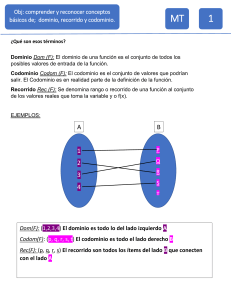
FUNCIÓN INVERSA
3-Analice si la inversa de la función es o no es función:
3-1)
3-2)
Respuesta: La inversa de la función que corresponde al apartado 3-1) es función porque cada valor del
dominio tiene un único correspondiente en el codominio
y viceversa. La inversa de la función que
corresponde al apartado 3-2) no es función porque un valor del codominio es correspondiente de dos valores
del dominio.
4- Diga cuáles de las funciones del ejercicio anterior son biunívocas. Justifique su respuesta.
Respuesta: La función del apartado 3-1) es biunívoca porque cada elemento del codominio es el
correspondiente de un único elemento del dominio.