Propiedades de las funciones
Anuncio
PROPIEDADES DE LAS FUNCIONES
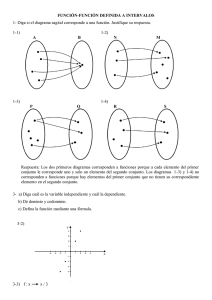
INYECTIVIDAD: Una función presenta esta propiedad si los elementos del codominio que están
asociados con los elementos del dominio, lo hacen en proporción uno a uno.
Ejemplo:
SUPRAYECTIVIDAD: Una función presenta esta propiedad si todos los elementos del codominio son
imagen de al menos un elemento del dominio.
Ejemplo:
BIYECTIVIDAD: Una función presenta esta propiedad, si cumple con las dos propiedades anteriores.
Ejercicio: Sea el conjunto A = {1, 2, 3, 4, 5} y la regla de correspondencia y = x + 2
Realizar lo siguiente:
• Construir el diagrama sagital correspondiente.
• Determinar si la relación es una función.
• Determinar la imagen de la función.
• ¿Qué propiedades presenta la función?
• Determinar si la relación inversa es función.
Y=x+2
Y=1+2=3
Y=2+2=4
Y=3+2=5
Y=4+2=6
Y=5+2=7
X=y−2
X=3−2=1
X=4−2=2
X=5−2=3
X=6−2=4
X=7−2=5
TAREA DE MATEMÃTICAS IV
1
SEA EL CONJUNTO A=(−2,−1,0,1,2,) Y LA REGLA DE CORRESPONDENCIA Y=X2−2
• CONSTRUIR EL DIAGRAMA SAGITAL CORRESPONDIENTE
• DETERMINAR LA IMAGEN DE LA FUNCIÓN
• DETERMINAR SI LA RELACIÓN ES UNA FUNCIÓN
• QUE PROPIEDADES PRESENTA LA FUNCIÓN
• DETERMINAR SI LA RELACIÓN INVERSA ES UNA FUNCIÓN
2
![Exame Diagnostico[1].docx(cuestionario)](http://s2.studylib.es/store/data/002783767_1-2569e068c89b83f16ea362597930d478-300x300.png)
