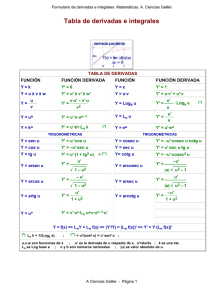
Relaciones pitagóricas tg 1 sec cotg 1 sen ccooesc 1 s α +

RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO EN UN TRIÁNGULO RECTÁNGULO. Considerando el triángulo rectángulo  ABC , las razones trigonométricas del ángulo   son las siguientes: VALORES DE LAS RAZONES CIRCULARES DE ÁNGULOS NOTABLES grados
0º
radianes
0
sen
0
cos
1
tg
0
cotg
*
3
sec
1
2 3
3
cosec
*
2
cat. op.
hip.
cosec  
hip.
cat.op.
cat. ady.
hip.
cos  
sec  
hip.
cat. ady.
sen  
tg  
cat. op.
cat. ady.
cotg  
cat. ady.
cat. op.
Los símbolos sen, cos, tg (tan), se leen, respectivamente: seno, coseno y tangente. Los símbolos sec, cosec (csc), cotg (cot), se leen: secante, cosecante y cotangente. En un triángulo rectángulo la longitud de la hipotenusa es mayor que la de cualquiera de los catetos, luego el valor del seno o del coseno será menor que 1 siempre. Los seis elementos principales en todo triángulo son sus tres lados y sus tres ángulos. Cuando se conocen tres de estos elementos, con tal que al menos uno de ellos sea un lado, la trigonometría enseña a solucionar el triángulo, es decir, a encontrar el valor de los otros tres elementos. 30º

6
1
2
3
2
3
3
45º

4
2
2
2
2
FUNCIONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA EN LA CIRCUNFERENCIA TRIGONOMÉTRICA. y
r
x
cos  
r
y
tg  
x
cosec  
 x  0, y  0 del denominador
S
sen 2   cos 2   1
tg   1  sec 
2
2
cotg 2   1  cosec2 
2
(90º )
sen   2     cos  cosec   2     sec 
cos   2     sen  sec   2     cosec 
tg   2     cotg  cotg   2     tg 
Ángulos del 3º Cuadrante
sen        sen  cosec        cosec 
cos        cos  sec        sec 
tg       tg 
cotg       cotg 
1
0
1
*
0
1
3
3
0
*
0
*
2
2
*
1
*
1
2
2 3
3
1
*
1
*
El área de un triángulo es la mitad del producto
de una base por la altura correspondiente.
El área de un triángulo es el semiproducto de dos
de sus lados por el seno del ángulo que forman.
El área de un triángulo es el cociente entre el
producto de sus lados y cuatro veces el radio
de su circunferencia circunscrita.
El área de un triángulo es igual al producto del radio
de la circunferencia inscrita por su semiperímetro.
Fórmula de Herón
R : radio de la circunferencia circunscrita. 
r:
R
radio de la circunferencia inscrita.
p : semiperímetro.  p 
abc
2
r
a
b
c


2sen  2sen  2sen 
 p  a  p  b  p  c 
p
TEOREMAS Teorema de los senos : En todo triángulo, cada lado es directamente
a
b
c


sen  sen  sen 
2
y  arc sen x  x  sen y
Teorema del coseno : En un triángulo, el cuadrado de cada lado es igual
a la suma de los cuadrados de los otros dos menos el doble producto de ambos
por el coseno del ángulo que forman.
sen 1 x  arc sen x
a 2  b 2  c 2  2bc  cos 
Teorema de las tangentes :
¡ cuidado en la calculadora !
b 2  a 2  c 2  2ac  cos 

tg
ab
2


a  b tg  
2
c 2  a 2  b 2  2ab  cos 
Ángulos del 2º Cuadrante
sen       sen 
cosec       cosec 
tg        tg 
cotg        cotg 
cos        cos  sec        sec 
Ángulos del 4º Cuadrante
sen      sen  cosec      cosec 
cos     cos 
sec     sec 
tg      tg 
cotg      cotg 
Ángulos mayores de 2
sen    2k    sen  cosec    2k    cosec 
750 360
 2 vueltas + 30º
30 2
0

REDUCCIÓN AL PRIMER CUADRANTE Ángulos COMPLEMENTARIOS
0
proporcional al seno del ángulo opuesto.
pero sen 2   sen  2

1
0
p  p  a  p  b  p  c 
¡ atención !
sen 2   sen   sen    sen  
0
*
a bc
4R
Relaciones pitagóricas
1
3
S r p
1
r

sen  y
1
r
sec  

cos  x
1
x
cotg  

tg  y
sen 
tg  
cos 
x : abscisa , y : ordenada , r : radio
sen  
S
90º 180º 270º 360º

3

2
2
2
1
ÁREA DE UN TRIÁNGULO base  altura
S
2
1
S  b  c  sen 
2
60º

3
3
2
1
2
cos    2k    cos  sec    2k    sec 
tg    2k    tg 
cotg    2k    cotg 
En un TRIÁNGULO RECTÁNGULO Teorema
2
2
2
de Pitágoras: a  b  c
Teorema
del cateto:
b2  a  m
Teorema
de la altura:
h2  m  n
bc  ah
c2  a  n
Trigonometría – H2 (cc) www.3con14.com