Ejercicios

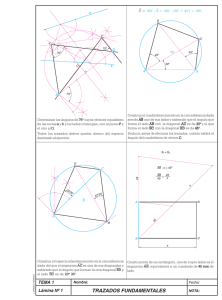
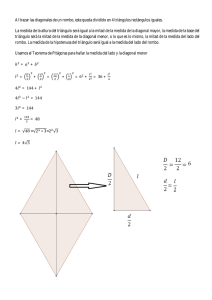
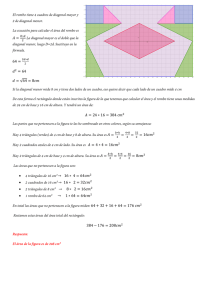
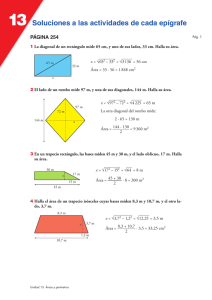
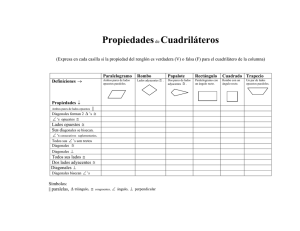
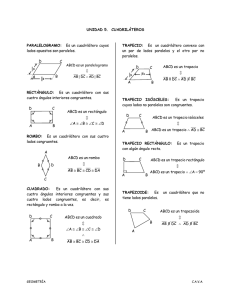
Ejercicios - 3
Cuadriláteros
Enviar al Tutor los ejercicios 1, 5 y 7,
1–
Construir un cuadrilátero ABCD (sentido ABC horario) conociendo la diagonal BD de 5 cm,
los ángulos A y C de 60º y 90º respectivamente y sabiendo que las diagonales se cortan en
el punto medio de BD, formando un ángulo de 75º.
2–
Construir un paralelogramo conociendo:
a) dos lados consecutivos y una diagonal.
b) dos lados consecutivos y un ángulo.
c) un lado, una diagonal y un ángulo.
d) un lado y las dos diagonales.
3–
Construir un trapecio ABCD (sentido ABC horario y lado AB paralelo al CD) conociendo:
a) AB, AD, BC y AC.
b) AB, AD, CD y AC.
c) AB, AD, CD y BAD.
d) CD, AD, CDA, ABC.
e) AB, CD, CDA, ABC.
4–
a)
b)
c)
d)
e)
5–
a) Demostrar que los puntos medios de los lados de un cuadrilátero cualquiera son vértices
de un paralelogramo.
b) ¿Qué condición deben cumplir las diagonales de dicho cuadrilátero, para que ese
paralelogramo sea:
1 – rectángulo?
2 – rombo?
3 – cuadrado?
6–
a) Demostrar que la condición necesaria y suficiente para que un cuadrilátero convexo sea
inscriptible, es que dos ángulos opuestos sean suplementarios.
b) Demostrar que la condición necesaria y suficiente para que un cuadrilátero convexo sea
circunscriptible, es que las sumas de los lados opuestos sean iguales.
Construir un rombo conociendo el lado y una diagonal.
Construir un rombo conociendo el lado y un ángulo.
Construir un rombo conociendo una diagonal y un ángulo.
Construir un rombo conociendo las dos diagonales.
Construir un cuadrado conociendo la suma de la diagonal y el lado.
Ver: “Curso de Geometría métrica” Tomo 1 – Pedro Puig Adam
Euler libros - Gómez Puig, Ediciones – Madrid
Lección 15.
7-
Sobre los lados CB, CA y AB de un triángulo cualquiera, se toman respectivamente los
puntos P, Q y R arbitrarios. Demostrar que las circunferencias determinadas por los puntos
PQC, PRB y RQA tienen un punto común.
8–
Demostrar que la condición necesaria y suficiente para que un trapecio sea inscriptible, es
que sea isósceles.
9–
Construir un trapecio inscripto en una circunferencia de radio dado, conociendo la altura y la
diferencia de las bases.