© Abel Martín Una empresa fabrica dos tipos de piezas: A y B. Cada

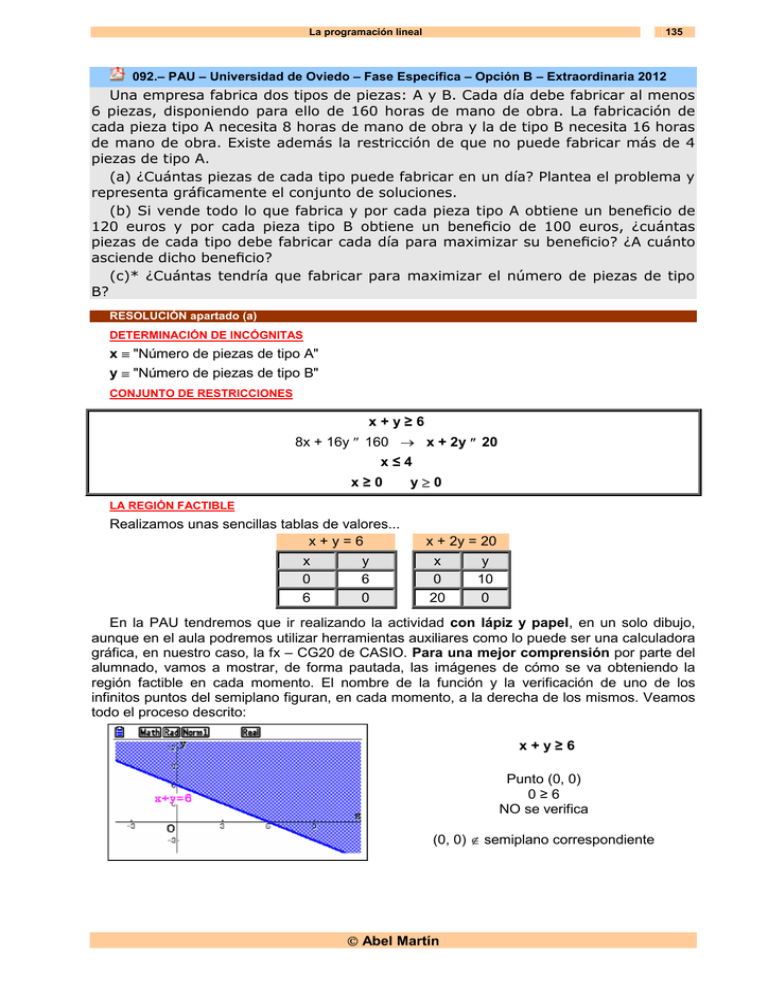
La programación lineal
135
092.– PAU – Universidad de Oviedo – Fase Específica – Opción B – Extraordinaria 2012
Una empresa fabrica dos tipos de piezas: A y B. Cada día debe fabricar al menos
6 piezas, disponiendo para ello de 160 horas de mano de obra. La fabricación de
cada pieza tipo A necesita 8 horas de mano de obra y la de tipo B necesita 16 horas
de mano de obra. Existe además la restricción de que no puede fabricar más de 4
piezas de tipo A.
(a) ¿Cuántas piezas de cada tipo puede fabricar en un día? Plantea el problema y
representa gráficamente el conjunto de soluciones.
(b) Si vende todo lo que fabrica y por cada pieza tipo A obtiene un beneficio de
120 euros y por cada pieza tipo B obtiene un beneficio de 100 euros, ¿cuántas
piezas de cada tipo debe fabricar cada día para maximizar su beneficio? ¿A cuánto
asciende dicho beneficio?
(c)* ¿Cuántas tendría que fabricar para maximizar el número de piezas de tipo
B?
RESOLUCIÓN apartado (a)
DETERMINACIÓN DE INCÓGNITAS
x ≡ "Número de piezas de tipo A"
y ≡ "Número de piezas de tipo B"
CONJUNTO DE RESTRICCIONES
x+y≥6
8x + 16y ≤ 160 → x + 2y ≤ 20
x≤4
x≥0
y≥0
LA REGIÓN FACTIBLE
Realizamos unas sencillas tablas de valores...
x+y=6
x
0
6
y
6
0
x + 2y = 20
x
0
20
y
10
0
En la PAU tendremos que ir realizando la actividad con lápiz y papel, en un solo dibujo,
aunque en el aula podremos utilizar herramientas auxiliares como lo puede ser una calculadora
gráfica, en nuestro caso, la fx – CG20 de CASIO. Para una mejor comprensión por parte del
alumnado, vamos a mostrar, de forma pautada, las imágenes de cómo se va obteniendo la
región factible en cada momento. El nombre de la función y la verificación de uno de los
infinitos puntos del semiplano figuran, en cada momento, a la derecha de los mismos. Veamos
todo el proceso descrito:
x+y≥6
Punto (0, 0)
0≥6
NO se verifica
(0, 0) ∉ semiplano correspondiente
 Abel Martín
Del aula a la PAU
136
x + 2y ≤ 20
(0, 0)
0 ≤ 20
SÍ se verifica
(0, 0) ∈ semiplano correspondiente
x≤4
0≤4
(0, 0) ∈ semiplano correspondiente
x≥0
Todos los valores del primero y cuarto
cuadrantes
y≥0
Todos los valores del primero y segundo
cuadrantes
Finalmente podremos observar la solución del sistema de inecuaciones en forma de zona
sombreada, los vértices y los nombres de las rectas.
Las distintas combinaciones de piezas fabricadas en un día vienen representadas por
los puntos (x, y) pertenecientes a la región factible (sombreada), donde "x" es número de
piezas de tipo A e "y" es el número de piezas de tipo B, con la condición de que tanto "x"
como "y" sean números naturales.
RESOLUCIÓN apartado (b)
Si vende todo lo que fabrica y por cada pieza tipo A obtiene un beneficio de 120 euros y por
cada pieza tipo B obtiene un beneficio de 100 euros, ¿cuántas piezas de cada tipo debe fabricar
cada día para maximizar su beneficio? ¿A cuánto asciende dicho beneficio?
B(x, y) = 120x + 100y
LOCALIZACIÓN DE SOLUCIONES
Teorema fundamental de la programación lineal: Como la región factible existe y está
acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono
que limita la región, o a lo largo de uno de los lados.
Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono
que constituye la región factible:
CÁLCULO DE VÉRTICES
A → Visualización directa en la gráfica y tabla de valores: A(0, 6)
B → Visualización directa en la gráfica y tabla de valores: B(0, 10)
C(4, y) Resolvemos el sistema
x=4 

x + 2 y = 20
→ 4 + 2y = 20
→ 2y = 16 → y = 8
x = 4 → y = 8 → C(4, 8)
 Abel Martín
La programación lineal
137
D(4, y) Resolvemos el sistema
x = 4

x + y = 6
→ 4+y=6
→ y=2
x = 4 → y = 2 → D(4, 2)
LA FUNCIÓN OBJETIVO
B(x, y) = 120x + 100y
ANÁLISIS DE ÓPTIMOS
Aplicamos el TEOREMA mencionado:
Vértices
A(0, 6)
B(0, 10)
C(4, 8)
D(4, 2)
B(x, y) = 120x + 100y
120·0 + 100·6 =
120·0 + 100·10 =
120·4 + 100·8 =
120·4 + 100·2 =
Valor
600
1000
1280
680
Para maximizar los beneficios tendrá que fabricar diariamente 4 piezas del tipo A y 8
del tipo B, momento en el que dichos beneficios ascenderán a 1280 euros.
RESOLUCIÓN apartado (c)*
¿Cuántas tendría que fabricar para maximizar el número de piezas de tipo B?
Para contestar a la pregunta, habrá que observar cuál es el mayor valor que toma "y" dentro
de la región factible.
Vemos que se encuentra en el punto D(0, 10)
Para maximizar el número de piezas del tipo B habrá que fabricar 10 de este tipo B y
ninguna del tipo A.
Criterios de corrección y calificación especificados en la prueba oficial:
(a) Plantear las inecuaciones: 0.75 puntos. Representar la región factible: 0.75 puntos.
Encontrar la combinación: 0.50 puntos. Cuestión: 0.5 puntos.
 Abel Martín
(b)