49 Representaciones Matriciales: > Podemos obtener

Representaciones Matriciales:
Podemos obtener representaciones matriciales que mimeticen las
operaciones del grupo de varias maneras.
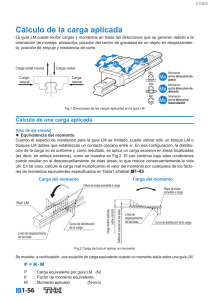
Una de ellas consiste en determinar el efecto que tienen las
operaciones de simetría sobre las coordenadas de un punto o
vector de posición en la molécula.
P (x1,x2,x3)
x3
x2
x1
Vamos a considerar que efecto tienen las diferentes operaciones
de simetría sobre las coordenadas de este punto:
Rotación de un ángulo θ respecto el eje z
y
(x,y,z)
α
x
θ
(x’,y’,z’)
49
x' = rcos(α − θ) = r(cosα cosθ + sinα sinθ ) = cosθ x + sinθ y
y' = r sin(α − θ) = r(sinα cosθ − cosα sinθ ) = − sinθ x + cosθ y
z' = z
En forma matricial:
 x´   cosθ sinθ 0  x 
 
  
 y´ =  - sinθ cosθ 0  y 
 z´   0
0
1  z 
  
De la misma manera, las rotaciones respecto al eje x e y se expresan:
0
0  x 
 x´   1
 
  
=
y
´
0
cosθ
sinθ
 y 
  
 z´   0 - sinθ cosθ  z 
 
  
 x´   cosθ 0 sinθ  x 
 
  
=
y
´
0
1
0
 y 
  
 z´   - sinθ 0 cosθ  z 
 
  
Reflexión respecto a un plano de simetría en el plano xy.
x' = x
y' = y
z' = − z
 x´   1 0 0  x 
 
  
 y´ =  0 1 0  y 
 z´   0 0 - 1 z 
 
  
Los puntos sobre el plano no se ven afectados mientras que la
coordenada perpendicular a él se invierte. De manera análoga se
definirían las matrices asociadas a una reflexión respecto a planos xz
o yz.
50
Inversión
respecto
centro
de
simetría
(en
el
centro
de
coordenadas)
x' = − x
y' = − y
z' = − z
 x´   - 1 0 0  x 
 
  
 y´ =  0 - 1 0  y 
 z´   0 0 - 1 z 
 
  
Rotación impropia respecto de un ángulo θ respecto el eje z
x' = rcos(α − θ) = r(cosα cosθ + sinα sinθ ) = cosθ x + sinθ y
y' = r sin(α − θ) = r(sinα cosθ − cosα sinθ ) = − sinθ x + cosθ y
z' = − z
 x´   cosθ sinθ 0  x   1 0 0  cosθ sinθ 0  x 
 

  
  
=
=
sinθ
cosθ
0
y
´
sinθ
cosθ
0
y
0
1
0
 y 

  
  
 z´   0
0
1  z 
0
- 1 z   0 0 - 1 0
  
Identidad
 x´   1 0 0  x 
 
  
 y´ =  0 1 0  y 
 z´   0 0 1  z 
 
  
x' = x
y' = y
z' = z
Para un grupo puntual, el conjunto de las matrices asociadas a cada
una de las operaciones de simetría forman una representación del
grupo, que denominaremos por la letra Γ.
En este caso, el tipo de representación basada en el efecto de las
operaciones de simetría sobre las coordenadas de un punto se suele
denominar Γxyz.
51
Ejemplo: Γxyz del grupo C2v.
Las operaciones de simetría del grupo son E, C2, σv(xz) y σv´(yz).
La matriz asociada a la operación identidad es siempre
1 0 0


D( E ) ≡  0 1 0 
 0 0 1


Para la rotación respecto al eje z tenemos
 cos(180) sin(180) 0   - 1 0 0 

 

D(C2 ) ≡  - sin(180) cos(180) 0  =  0 - 1 0 

0
0
1   0 0 1 

Las reflexiones respecto a los plano xz e yz quedan
1 0 0


D(σ xz ) ≡  0 - 1 0 
 0 0 1


- 1 0 0


D(σ yz ) ≡  0 1 0 
 0 0 1


Por tanto la representación matricial Γxyz es la formada por las
cuatro matrices Γxyz = { D(E), D(C2), D(σ(xz) , Dσ(yz) }
Estas 4 matrices cumplen la Tabla de multiplicación del grupo. Por
ejemplo podemos comprobar que σv(yz) ≡ σv(xz)·C2.
 1 0 0  - 1 0 0   - 1 0 0 

 


0
1
0
0
1
0
≡
0
1
0

 


 0 0 1  0 0 1   0 0 1 

 


σ ( xz ) ·
C2
≡ σ ( yz )
52
Otras representaciones matriciales:
Podemos generar otras representaciones matriciales de un grupo por
ejemplo determinando el efecto de las operaciones de simetría sobre
un conjunto de vectores centrados en los átomos de la molécula,
dando lugar a la representación Γ3N.
También podemos usar como base para la representación conjuntos
de funciones. Un ejemplo seria el uso de orbitales atómicos de los
átomos de la molécula
Existen pues, infinitas representaciones matriciales de un grupo,
dependiendo de los elementos de base que se usen (vector posición,
vectores de base, orbitales atómicos, etc).
Representaciones de la misma dimensión (numero de elementos de
base) de un mismo grupo puntual se denominan equivalentes y
están relacionadas mediante una transformación de semejanza.
Existen representaciones cuyas matrices (para cada una de las
operaciones de simetría) resultan ser diagonales por bloques.
0
0
0
1

 0 −1 1/ 2 0
 0 −1/ 2 1
0

0
0 −1
0
0
0
0
0

0

0
0

0
0 
Éstas representaciones reciben el nombre de representaciones
irreducibles y son las más importantes ya que para ellas se aplican
una serie de teoremas derivados de la Teoria de Grupos.
53
Por ejemplo, la representación anterior Γxyz del grupo C2v consistía
en un conjunto de matrices 3x3 que eran diagonales (y por tanto
diagonales por bloques)
D(E)
D(C2)
D(σ(xz)
Dσ(yz)
 1 0 0


0 1 0
 0 0 1


-1 0 0


 0 -1 0
 0 0 1


1 0 0


0 - 1 0
 0 0 1


- 1 0 0


 0 1 0
 0 0 1


Por tanto, se dice que la representación Γxyz es reducible. Y las
representaciones irreducibles de la que se compone son
D(E)
D(C2)
D(σ(xz)
Dσ(yz)
Γ(1)1
1
-1
1
-1
Γ(1)2
1
-1
-1
1
Γ(1)3
1
1
1
1
Γxyz = Γ(1)1 ⊕ Γ(1)2 ⊕ Γ(1)3
En éste caso particular las representaciones irreducibles de que se
compone
la
representacion
reducible
son
diferentes
y
monodimensionales, pero ninguna de estas dos condiciones son
necesarias en general.
En el caso que la representación reducible Γxyz no hubiera sido
diagonal por bloques, se debería haber buscado una base en la que
si lo fuera (mediante transformaciones de semejanza) y obtener
posteriormente las representaciones irreducibles.
Es esencial entender que no es tan importante saber cómo se
obtienen las representaciones irreducibles como el hecho de que
existen y que forma tienen.
54