1 EJC 16C: PROBABILIDAD LINEAL-LOGIT

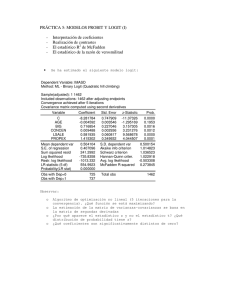
ECONOMETRIA 2 - ECON 3301 - SEMESTRE II - 08
Profesor: Ramón Rosales; [email protected]
Profesor Taller: William Delgado; [email protected]
Profesor Taller: Juan Carlos Vasquez; [email protected]
Profesor Taller: Diego Marino; [email protected]
Monitor: Alejandro Urrego; [email protected]
Monitor: Juan Sebastián Sánchez; [email protected]
Monitor: Francisco Correa; [email protected]
Monitor: Carlos Morales; [email protected]
EJC 16C: PROBABILIDAD LINEAL-LOGIT-PROBIT.
Wooldridge,
Considere una muestra de 1388 observaciones relacionada con el consumo de
cigarrillo en mujeres embarazadas. Mediante este ejercicio se desea analizar si
características socioeconómicas tales como la educación de la madre, la raza y el
ingreso familiar, inciden o ayudan a determinar la probabilidad de que una mujer
fume durante su embarazo. Para ello se estimarán los modelos de probabilidad
lineal, logit y probit.
Descripción de los datos
>emplos\MPL, logit, Probit\BWGHT.DTA
obs:
1,388
vars:
14
size:
55,520 (99.5% of memory free)
------------------------------------------------------------------------------storage display
value
variable name
type
format
label
variable label
------------------------------------------------------------------------------faminc
float %9.0g
1988 family income, $1000s
cigtax
float %9.0g
cig. tax in home state, 1988
cigprice
float %9.0g
cig. price in home state, 1988
bwght
int
%8.0g
birth weight, ounces
fatheduc
byte
%8.0g
father's yrs of educ
motheduc
byte
%8.0g
mother's yrs of educ
parity
byte
%8.0g
birth order of child
male
byte
%8.0g
=1 if male child
white
byte
%8.0g
=1 if white
cigs
byte
%8.0g
cigs smked per day while preg
lbwght
float %9.0g
log of bwght
bwghtlbs
float %9.0g
birth weight, pounds
packs
float %9.0g
packs smked per day while preg
lfaminc
float %9.0g
log(faminc)
------------------------------------------------------------------------------Sorted by:
Se tiene la variable cualitativa si la mujer fumaba o no durante el embarazo. En este caso si fuma
se asigna 1 y cero en caso contrario.
El Modelo de Probabilidad lineal
. reg smokes motheduc white lfaminc
Source |
SS
df
MS
-------------+-----------------------------Model | 11.3314741
3 3.77715803
Residual | 168.264777 1383 .121666505
-------------+-----------------------------Total | 179.596251 1386 .129578825
Number of obs
F( 3, 1383)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
1387
31.05
0.0000
0.0631
0.0611
.34881
1
-----------------------------------------------------------------------------smokes |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------motheduc | -.0293207
.0043342
-6.76
0.000
-.0378229
-.0208184
white |
.048364
.0243837
1.98
0.048
.0005309
.096197
lfaminc | -.0427425
.0119231
-3.58
0.000
-.0661318
-.0193532
_cons |
.6255033
.0537477
11.64
0.000
.5200675
.730939
------------------------------------------------------------------------------
Uno de los problemas con el modelo de probabilidad lineal es que las probabilidades predichas
pueden ser menores que cero o mayores que uno y que los efectos marginales son constantes.
Predicción de las probabilidades del Modelo de probabilidad lineal.
. predict smo1
(option xb assumed; fitted values)
(1 missing value generated)
. sum smokes smo1
Variable |
Obs
Mean
Std. Dev.
Min
Max
-------------+-------------------------------------------------------smokes |
1388
.1527378
.3598642
0
1
smo1 |
1387
.1528479
.0904194 -.0806922
.615532
Note en este caso que existen probabilidades predichas por debajo de cero
El Modelo logit
. logit smokes motheduc white lfaminc
Iteration
Iteration
Iteration
Iteration
Iteration
0:
1:
2:
3:
4:
log
log
log
log
log
likelihood
likelihood
likelihood
likelihood
likelihood
=
=
=
=
=
-593.10529
-551.1645
-548.74295
-548.73367
-548.73367
Logistic regression
Log likelihood = -548.73367
Number of obs
LR chi2(3)
Prob > chi2
Pseudo R2
=
=
=
=
1387
88.74
0.0000
0.0748
-----------------------------------------------------------------------------smokes |
Coef.
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------motheduc | -.2518731
.0372045
-6.77
0.000
-.3247925
-.1789536
white |
.3438842
.2002178
1.72
0.086
-.0485355
.7363038
lfaminc | -.2962299
.0866347
-3.42
0.001
-.4660308
-.1264289
_cons |
2.012535
.4474219
4.50
0.000
1.135604
2.889466
------------------------------------------------------------------------------
Predicción de las probabilidades del Modelo logit.
. predict smo2
(option p assumed; Pr(smokes))
(1 missing value generated)
. sum smokes smo1 smo2
2
Variable |
Obs
Mean
Std. Dev.
Min
Max
-------------+-------------------------------------------------------smokes |
1388
.1527378
.3598642
0
1
smo1 |
1387
.1528479
.0904194 -.0806922
.615532
smo2 |
1387
.1528479
.0950377
.0228038
.8588936
Ahora las probabilidades predichas están entre cero y uno.
Graficando la función de probabilidad del modelo Logit.
Primero se genera en vector X por BETA
. gen xbeta=2.012535-.2518731*motheduc+.3438842*white-.2962299*lfaminc
Luego se genera la función de probabilidad.
. gen fxbeta=exp(xbeta)/(1+(exp(xbeta)))
Se ordena la variable xbeta para posteriormente graficar la función de distribución de probabilidad
versus xbeta.
. sort xbeta
. twoway connected fxbeta xbeta
Los efectos marginales debido a un cambio en xbeta no son constantes. El efecto parcial es más
grande cuando xbeta es cero y más pequeño a medida que xbeta se acerca a – infinito y a +
infinito.
Efectos marginales del modelo logit
. mfx
Marginal effects after logit
y = Pr(smokes) (predict)
= .13170934
3
-----------------------------------------------------------------------------variable |
dy/dx
Std. Err.
z
P>|z| [
95% C.I.
]
X
---------+-------------------------------------------------------------------motheduc | -.0288047
.00401
-7.18
0.000
-.03667 -.02094
12.9358
white*|
.0366196
.01981
1.85
0.065 -.002205 .075444
.784427
lfaminc | -.0338774
.00984
-3.44
0.001 -.053173 -.014582
3.07203
-----------------------------------------------------------------------------(*) dy/dx is for discrete change of dummy variable from 0 to 1
El Modelo probit
. probit smokes motheduc white lfaminc
Iteration
Iteration
Iteration
Iteration
0:
1:
2:
3:
log
log
log
log
likelihood
likelihood
likelihood
likelihood
=
=
=
=
-593.10529
-547.59879
-546.77099
-546.76991
Probit regression
Log likelihood = -546.76991
Number of obs
LR chi2(3)
Prob > chi2
Pseudo R2
=
=
=
=
1387
92.67
0.0000
0.0781
-----------------------------------------------------------------------------smokes |
Coef.
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------motheduc | -.1450599
.0207899
-6.98
0.000
-.1858074
-.1043124
white |
.1896765
.1098804
1.73
0.084
-.0256852
.4050382
lfaminc | -.1669109
.0498894
-3.35
0.001
-.2646923
-.0691296
_cons |
1.126276
.2504608
4.50
0.000
.6353822
1.617171
------------------------------------------------------------------------------
Predicción de las probabilidades del Modelo probit.
. predict smohat
(option p assumed; Pr(smokes))
(1 missing value generated)
. sum smokes smo1 smo2 smohat
Variable |
Obs
Mean
Std. Dev.
Min
Max
-------------+-------------------------------------------------------smokes |
1388
.1527378
.3598642
0
1
smo1 |
1387
.1528479
.0904194 -.0806922
.615532
smo2 |
1387
.1528479
.0950377
.0228038
.8588936
smohat |
1387
.152034
.0962422
.0145713
.8404884
Las probabilidades predichas están entre cero y uno.
Efectos marginales del modelo probit
. mfx
Marginal effects after probit
y = Pr(smokes) (predict)
= .13260473
-----------------------------------------------------------------------------variable |
dy/dx
Std. Err.
z
P>|z| [
95% C.I.
]
X
---------+-------------------------------------------------------------------motheduc |
-.03111
.0043
-7.24
0.000 -.039531 -.022689
12.9358
white*|
.0382706
.02081
1.84
0.066 -.002522 .079063
.784427
lfaminc | -.0357962
.01069
-3.35
0.001
-.05675 -.014842
3.07203
-----------------------------------------------------------------------------(*) dy/dx is for discrete change of dummy variable from 0 to 1
4
Porcentaje de pronósticos correctos en el modelo probit
. gen py=smohat>0.5
. table py smokes, contents( freq )
-----------------------|
smokes
py |
0
1
----------+------------0 | 1,166
210
1 |
10
2
------------------------
El porcentaje de pronósticos correctos es la suma de los elementos de la diagonal de esta tabla
sobre el total de observaciones.
.
.
.
end of do-file
.
5