Clase 11 - Angelfire

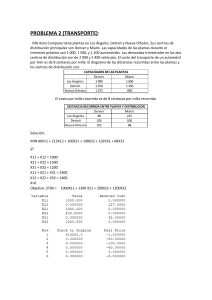
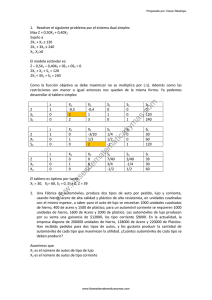
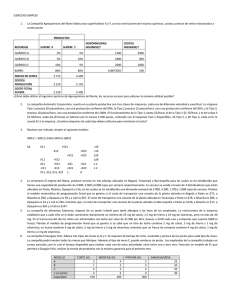
Modelos de Transporte:
método de la esquina
noroeste
M. En C. Eduardo Bustos Farías
Problemas de transporte
Surge cuando se necesita un modelo costo-efectividad
que permita transportar ciertos bienes desde un lugar
de origen a un destino que necesita aquellos bienes ,
con ciertas restricciones en la cantidad que se puede
transportar.
Se presenta al planear la distribución de bienes y
servicios desde varias localizaciones de suministro
hacia varias ubicaciones de la demanda.
La cantidad de los bienes disponibles en cada
localización de su ministro (origen) es limitada, y la
cantidad de los bienes necesarios en cada una de las
localizaciones de demanda (destino) es conocida.
El objetivo es minimizar el costo de embarcar los bienes2
desde los orígenes hasta los destinos.
Q
Q
Q
Dentro de la amplia gama de problemas de
programación lineal se encuentran los problemas de
transporte, los cuales poseen características
particulares.
En este caso específico de problemas, es necesario
determinar la ruta más eficiente para hacer llegar
productos o materiales desde puntos alternativos de
origen hasta diferentes puntos de destino,
cumpliendo las restricciones específicas de oferta y
demanda y con base en la estructura de costos de las
rutas de transporte.
Las diversas técnicas para abordar el problema de
transporte requieren de una tabla de transporte,
dicha tabla en su forma estándar registra todos los
elementos esenciales del problema de transporte que
estamos solucionando: costos de transporte; puntos
de origen y destino, cantidades de oferta y demanda;
tal y como se muestra a continuación:
3
En la tabla anterior la demanda (33) es igual a la oferta (33), lo cual significa
que el problema está balanceado y ello facilita la búsqueda de la solución.
4
Definición del problema
* Se tienen m lugares de origen. Cada lugar de origen tiene
una capacidad de producción Si
*Se tienen n destinos. Cada destino j demanda Dj
*Objetivo:
Minimizar el costo de transporte de la carga al lugar de destino
cumpliendo con las restricciones de los lugares de origen.
5
Caso I.
Oferta igual a demanda
6
EJEMPLO 1
Farmacéutica Carlton
Problema de transporte
7
Farmacéutica Carlton
La farmacéutica Carlton abastece de medicamentos y
otros suministros médicos.
Esta tiene tres plantas en: Claveland, Detroit,
Greensboro.
Tiene cuatro centros de distribución en: Boston,
Atlanta, St Louis y Richmond.
La gerencia de Carlton desea realizar el transporte de
sus productos de la manera más económica posible.
8
Datos
Costo de transporte por unidad, oferta y demanda.
Desde
Cleveland
Detroit
Greensboro
Demanda
Boston
$35
37
40
1100
Richmond
30
40
15
400
Hacia
Atlanta
40
42
20
750
St. Louis
32
25
28
750
Oferta
1200
1000
800
Supuestos
* El costo de transporte por unidad es constante
* Todos los transportes ocurren simultáneamente.
* Solo se considera el costo de transporte entre el lugar de
origen y el de destino
* La oferta total es igual a la demanda total.
9
SOLUCIÓN
10
RED QUE REPRESENTA
EL PROBLEMA
Origenes
Destinos
D1=1100
Boston
35
Cleveland
S1=1200
30
40
32
37
Detroit
S2=1000
25
35
Greensboro
S3= 800
40
42
D2=400
Atlanta
15
20
28
Richmond
D3=750
St.Louis
D4=750 11
Modelo matemático
* La estructura del modelo es la siguiente:
Minimizar <Costo total de transporte>
sujeto a :
cantidad a transportar desde la fabrica = oferta de la fábrica
cantidad a recibir por la distribuidora = demanda de la
distribuidora.
* Variables de decisión:
Xij = cantidad a transportar desde la fábrica i a la
distribuidora j
donde i = 1(Claveland), 2(Detroit), 3(Greensboro)
j = 1(Boston), 2(Richmond), 3(Atlanta), 4 (St,Louis)
12
Oferta de Cleveland X11+X12+X13+X14 = 1200
de la Oferta
OfertaRestricciones
de Detroit X21+X22+X23+X24
= 1000
Boston
Oferta de Greensboro X31+X32+X33+X34 = 800
D1=1100
X11
Cleveland
S1=1200
X12
X13
X21
X31
Richmond
X14
X22
Detroit
S2=1000
D2=400
X32
X23
X24
Atlanta
X33
St.Louis
Greensboro
S3= 800
D3=750
X34
D4=75013
El modelo matemático completo
Restriccione de la oferta:
X11+ X12+ X13+ X14
1200
1000
800
X21+ X22+ X23+ X24
X31+ X32+ X33+ X34
Restricciones de la demanda:
X11+
X21+
X12+
X22+
X13+
X14+
=
=
= 1000
X31
X32
X23+
400
= 750
= 750
X33
X24+
X34
=
=
Todos los Xij mayores que cero
14
Solución optima obtenida a través de Excel
FARMACUETICA CARLTON
COSTOS UNITARIOS
BOSTON RICHMOND ATLANTA ST.LOUIS
$
35,00 $
30,00 $
40,00 $
32,00
CLEVELAND
$
37,00 $
40,00 $
42,00 $
25,00
DETROIT
40,00 $
15,00 $
20,00 $
28,00
GREENSBORO $
DEMANDAS
1100
400
750
750
ALTERNATIVAS DE TRANSPORTE
BOSTON RICHMOND ATLANTA ST.LOUIS
850
350
0
0
CLEVELAND
250
0
0
750
DETROIT
0
50
750
0
GREENSBORO
TOTAL
1100
400
OFERTAS
1200
1000
800
750
TOTAL
1200
1000
800
750
COSTO TOTAL =
84000
15
Análisis
Análisisde
deSensibilidad
Sensibilidadpor
porWINQSB
WINQSB
Si utilizamos esta ruta, el costo total
mo
i
t
aumentara en $5 por unidad
Op
o
ng
a
transportada.
R
16
Ra
ng
od
ef
ac
tib
ilid
ad
Precio sombra de la distribuidora - el costo de mandar una unidad más por la
distribuidora.
Precio sombra de la planta - el costo de cada unidad extra disponible
en la planta.
17
Interpretación
de los resultados del
análisis de sensibilidad.
* Reducción de Costos:
- La cantidad a transportar que reduce
el costo por unidad entrega la ruta más
económicamente atractiva.
- Si una ruta debe usarse
obligatoriamente, incurriendo así
en
el costo que ello significa, por cada carga
transportada , el costo total aumentara en
una cantidad igual a la
reducción
del costo hecha.
18
* Precios Sombra:
- Para las plantas el precio sombra de
transporte
corresponde al costo de
cada unidad disponible en la
planta.
- Para las distribuidoras, el precio sombra
de transporte
corresponde al costo de
cada unidad extra demandada por
la
distribuidora.
19
EJEMPLO 2
Aplicación del problema de transporte a
planeación de la producción
20
Q
Q
Q
Q
La empresa Miller Electronics Co. Fabrica
videojuegos.
No tiene inventario inicial en octubre y en
diciembre no desea ningún inventario final.
Pueden fabricarse los juegos en horas
normales y en tiempo extra.
La demanda aumenta en diciembre, no puede
ser satisfecha con la sola producción de ese
mes, por lo que deben utilizarse inventarios
para transportar capacidad previa de
producción hacia el futuro.
21
22
Solución con winqsb
23
24
EJEMPLO 3
Compañía de ski Montpelier
Problema de transporte
25
Compañía de ski Montpelier
Usando un modelo de transporte para un
itinerario de producción
* Montpelier planea su producción de ski para los meses de
julio, agosto y septiembre.
* La capacidad de producción y el costo de producción unitario
puede varia de un mes a otro.
* La compañía puede destinar tiempo de producción adicional
para la fabricación de skis.
* El nivel de producción es capaz de satisfacer la demanda
proyectada y un trimestre del nivel de inventario.
* La gerencia desea un itinerario de producción que minimiza el
costo del trimestre.
26
Datos:
* Inventario inicial = 200 pares
* Nivel de inventario requerido = 1200 pares
* Nivel de producción para el próximo trimestre= 400 pares (tiempo normal)
200 pares (sobretiempo)
* La tasa de costo de almacenaje ed de 3% mensual por ski
* El nivel de producción, la demanda esperada para del trimestre, (en pares
de ski) y el costo de producción por unidad (por meses)
Meses
Julio
Agosto
Septiembre
Demanda
Esperada
400
600
1000
Capacidad de Producción Producción
Producción Tiempo Normal Sobretiempo
1000
25
30
800
26
32
400
29
37
27
Análisis de la demanada
* Demanda neta a satisfacer en Julio = 400 - 200 = 200 pares
en inventario
* Demanda neta de agosto = 600
* Demanda
neta
septiembre
= 1000 + 1200 = 2200 pares
Análisis de
losencostos
unitarios
demanda esperada
inventario req.
Costo Unitario= [costo unitario de producción] +
[costo
de almacenamiento por mes ][número de
An
álisisunitario
de la oferta
* La capacidad
de producción corresponde a la oferta
meses
en inventario]
* Existen dos tipos de “oferta”
Ejemplo: Una unidad producida en julio en tiempo normal y
1.- Oferta producida en tiempo normal (capacidad de producción)
vendida
en septiembre
25+. (3%)(25)(2 meses) =
2.- Oferta
producida en cuesta=
sobretiempo
$26.50
28
SOLUCIÓN
29
Producción
Mes/periodo
1000
800
400
400
Julio
S/T
Agst.
T/N
Agst.
S/T
Sept.
T/N
25
25.75
26.50
0
30
30.90
31.80 +M
0
Mes
Ventas
Julio
+M
26
+M
26.78
32
+M
0
Sept.
S/T
Agst..
600
Sept.
2200
Exceso
300
+M
32.96
0
200
+M
0
29
200
37
0
30
Demanda
Capacidad de Producción
500
July
Julio
R/T
T/N
Representación de la Red
Producción Julio: tiempo normal
Destino: Demanda para Julio
Costo Unitario= $25 (producción)
Producción Agosto:Sobretiempo
Destino: Demanda de Septiembre
32+(.03)(32)=$32.96
Costo Unitario =Producción+un mes de almacenamiento
31
Resumen de la solución óptima.
* En julio producir 1000 pares en tiempo normal y 500 pares en
sobretiempo (hrs. Extra).
Total Disponible : 1500 - 200 = 1300 a fines de julio
* En agosto producir 800 pares en tiempo normal y 500 en
sobretiempo. Disponibles = 800 + 300 - 600 = 500 pares
* En septiembre producir 400 pares en tiempo normal. Con
1000 pares para la posible demanda los cuales se pueden
distribuir:
(1300 + 500 ) + 400 - 1000 = 1200 pares disponibles
para ser transportados
a Ski Chalet.
Inventario + Producción - Demanda
32
EJEMPLO 4
FOSTER GENERATORS
Problema de transporte
33
Q
Se desea determinar cuanto de su
producción deberá embarcarse
desde cada una de las plantas
hasta cada centro de distribución
para minimizar el costo.
34
SOLUCIÓN
35
36
Solución
xij = número de unidades
embarcadas del origen i al destino
j.
i = 1, 2, 3
j = 1, 2, 3, 4
Función Objetivo:
Mín Z = 3x + 2 x + 7 x + 6 x + 7 x + 5x + 2 x + 3x + 2 x + 5x + 4 x
11
12
13
14
21
22
23
24
31
32
33
37
+ 5 x34
Restricciones:
Oferta
Demanda:
x11 + x12 + x13 + x14 ≤ 5000
x11 + x21 + x31 ≤ 6000
x21 + x22 + x23 + x24 ≤ 6000
x12 + x22 + x32 ≤ 4000
x31 + x32 + x33 + x34 ≤ 2500
x13 + x23 + x33 ≤ 2000
xij ≥ 0
∀i, j
x14 + x24 + x34 ≤ 1500
38
El modelo de transporte se
caracteriza por:
Q
Q
Q
Q
Las m restricciones de oferta y las n
restricciones de demanda son
ecuaciones lineales.
Se cumple la condición de no
negatividad.
La función objetivo es lineal.
Es un modelo de programación lineal
con m + n restricciones y m x n
variables.
39
Q
Para resolver la tabla de transporte
necesitamos una solución factible
básica inicial (SFBI)
40
SOLUCIÓN POR WINQSB
41
42
43
44
45
LA REGLA DE LA ESQUINA
NOROESTE
46
Esta regla nos permite encontrar una
solución factible básica inicial
(SFBI), una vez que tengamos el
problema de transporte
“balanceado” o equilibrado, es
decir que el total de ofertas iguales
al total de demandas.
47
PROCEDIMIENTO
Q
Q
Iniciar la asignación en el renglón 1 y
columna 1 (esquina noroeste) y formar una
base asignando cantidades a las rutas, de
forma tal que se agoten las existencias de la
fabrica y se satisfaga la demanda de los
mercados.
Así entonces, la asignación inicia en la casilla
X11 (esquina noroeste) y si lo fábrica 1 no
agotó su oferta continuara en la casilla X12 y
así sucesivamente.
48
Q
En el caso de que el total de la oferta
de la fabrica 1 no haya sido suficiente
para cubrir la demanda del mercado 1,
completar con la oferta de la fabrica 2,
que es la casilla X21 y si no se agotó la
oferta pasar a la casilla X22 y así
continuar hasta concluir el proceso de
asignación.
49
Con la forma anterior se conseguirá la
siguiente solución básica factible inicial:
x11
15
x21
x13
x14
30
x23
31
x33
x41
x42
x43
15
20
31
x24
9
x34
50
x44
25
84
45
x31
x12
15
x22
5
x32
50
25
50
Supuestos del método:
1.
2.
3.
4.
5.
6.
Asignamos lo más que podamos a la variable
x11 que ocupa la posición noroeste de la
tabla.
La oferta es igual a la demanda.
El proceso de asignar a la variable el mínimo
valor entre oferta y demanda disponibles se
repite hasta que toda la oferta y demanda
totales sean satisfechas.
Genera una solución factible básica inicial.
Las celdas en blanco corresponden a
variables no básicas y sus valores son cero.
Se obtienen variables básicas en las celdas
con asignación.
51
EJEMPLO 1
52
Encontrar la ruta de costo mínimo para el
siguiente problema de transporte, usando el
método de la esquina noroeste.
x11
x12
x13
x14
30
x21
x22
x23
x24
45
x31
x32
x33
x34
50
x41
x42
x43
x44
25
15
20
31
84
53
X11
x12
x13
x14
30 15
x21
x22
x23
x24
45
x31
x32
x33
x34
50
x41
x42
x43
x44
25
15
0
20
31
84
15
54
X11
X12
x13
x14
30 15 0
15
15
x21
x22
x23
x24
45
x31
x32
x33
x34
50
x41
x42
x43
x44
25
15
0
20
5
31
84
55
X11
X12
15
15
x21
X22
x13
x14
30 15 0
x23
x24
45 40
5
x31
x32
x33
x34
50
x41
x42
x43
x44
25
15
0
20
31
84
5
0
56
X11
X12
x13
x14
30 15 0
15
15
x21
X22
X23
X24
45 40 9
5
31
x31
x32
x33
x34
50
x41
x42
x43
x44
25
15
0
20
31
0
84
5
0
57
X11
X12
x13
x14
30 15 0
15
15
x21
X22
X23
X24
45 40 9 0
5
31
9
x31
x32
x33
x34
50
x41
x42
x43
x44
25
15
0
20
31
0
84
5
0
75
58
X11
X12
15
15
x21
x31
x13
x14
30 15 0
X22
X23
X24
45 40 9 0
5
31
9
x32
x33
X34
50 0
50
x41
x42
x43
x44
15
0
20
31
0
84
5
0
75
25
25
59
X11
X12
15
15
x21
x31
x13
x14
30 15 0
X22
X23
X24
45 40 9 0
5
31
9
x32
x33
X34
50 0
50
x41
x42
x43
X44
25 0
25
15
0
20
5
0
31
0
84
75
25
0
60
EJEMPLO 2
61
62
SOLUCIÓN
63
64
U
=+1-5+2-4=-6
65
66
67
68
Ejemplo 2
Método de la esquina noroeste
69
Q
Encontrar la ruta de costo mínimo
para el siguiente problema de
transporte, usando el método de la
esquina noroeste.
70
SOLUCIÓN
71
2
16
0
72
16
2
0
2,0
8
73
16
0
2
2,0
8
7
8
0
74
16
2
7
8
0
2,0
7,0
8
0
0
75
76
SFBI
Q
Q
Q
Q
Q
Q
Q
X11=16
X12=2
X13=0
X21=0
X22=8
X23=7
Costo= (16x6)+(2x5)+(2x8)+(4x7)=150
77
MEJORA DE LA SOLUCIÓN
78
79
80
81
82
Analicemos la adición hipotética
de 1 unidad a la variable X21:
1. Un aumento del costo debido al aumento de X21 en
una unidad por $4
2. Una disminución del costo debido a una disminución
de X11 en una unidad por $6
3. Un aumento del costo debido a un aumento de X12
en una unidad por $5
4. Una disminución del costo debido a una disminución
de X22 en una unidad por $2
El efecto neto es: 4 – 6 + 5 – 2 = +$1
Es evidente que no se quiere este efecto.
83
Analicemos la adición de la
variable X13 a la solución:
1. Un aumento del costo debido al aumento de
X13 en una unidad por $1
2. Una disminución del costo debido a la
disminución de X23 en 1 unidad por $4
3. Un aumento del costo debido al aumento de
X23 en 1 unidad por $2
4. Una disminución del costo debido a la
disminución de X12 en 1 unidad por $5
El efecto neto es: 1 – 4 + 2 – 5 = -$6
84
Hemos identificado una variable no –
básica (X13) que al volverse básica
tiene el efecto neto de disminuir el
costo total en $6 por cada unidad
remitida por esa ruta.
Q La asignación debe considerar las
restricciones, así tendríamos la
siguiente tabla:
Q
85
86
Como era de esperar, el costo total del
transporte se redujo en
$ 12 (150 – 12 = 138):
(6)(16) + (1)(2) + (2)(10) + (4)(5) =
96 + 2 + 20 + 20 = 138
87
Q
Q
Q
Evaluemos ahora la posibilidad de otro
intercambio entre las variables X11, X21, X23
y X13.
El efecto neto de un intercambio de una
unidad será: -6 + 4 – 4 +1 = -5 y el total de
unidades que se pueden intercambiar es de
cinco por lo tanto (-5)(5) = -25 por lo cual el
costo total del transporte se reduciría en $25
(138 – 25 = $ 113).
Así, la nueva tabla del transporte quedaría:
88
89
PROBLEMA PARA RESOLVER
Encontrar la ruta de costo mínimo para
el siguiente problema de transporte,
usando el método de la esquina
noroeste y el cálculo de los índices de
mejoramiento.
90
Plantear el modelo de red
Q Elaborar el modelo de programación
lineal asociado, sin resolverlo.
Q
91
SOLUCIÓN
92
X13+X23<=400
X14+X24<=350
93
PROBLEMA PARA RESOLVER
Encontrar la ruta de costo mínimo para
el siguiente problema de transporte,
usando el método de la esquina
noroeste y el cálculo de los índices de
mejoramiento.
94
Encontrar la ruta de costo mínimo para el
siguiente problema de transporte, usando el
método de la esquina noroeste.
Encontrar la SFBI, indicar su costo asociado.
Desde
Cleveland
Detroit
Greensboro
Demanda
Boston
$35
37
40
1100
Richmond
30
40
15
400
Hacia
Atlanta
40
42
20
750
St. Louis
32
25
28
750
Oferta
1200
1000
800
95
SOLUCIÓN
96
97
PROBLEMA PARA RESOLVER
Encontrar la ruta de costo mínimo para
el siguiente problema de transporte,
usando el método de la esquina
noroeste y el cálculo de los índices de
mejoramiento.
98
3
2
6
7
7
5
2
3
99
PROBLEMA PARA RESOLVER
Método de la esquina noroeste
100
La Red de AJax
Q
Q
Q
Q
Q
Q
La planta de Ajax se encuentra en Chicago.
Ajax vende sus computadoras en 8 mercados.
Para satisfacer la demanda de esta semana, el
gerente de Ajax debe decidir un plan de embarque
desde su planta hasta la bodega y los mercados.
Los costos de transporte se muestran en la tabla
Encontrar la ruta de costo mínimo para el
siguiente problema.
Usando el método de la esquina noroeste y el
cálculo de los índices de mejoramiento.
101
Costos de transporte $/unidad
Planta
1
2
3
4
5
7
8
oferta
1
14
24
21
20
21.5 19
17
30
100
2
24
15
28
20
18.5 19.5 24
28
45
demanda
22
14
18
17
15
20
6
13
15
102
EJERCICIO PARA RESOLVER
Encontrar la ruta de costo mínimo para
el siguiente problema.
Usando el método de la esquina
noroeste y el cálculo de los índices de
mejoramiento.
103
Almacenes
planta 1
2
3
4
oferta
1
464
513
654
867
75
2
352
416
690
791
125
3
995
682
388
685
100
demanda
80
65
70
85
300
Se desea saber cuántos camiones enviar de i a j dados los costos
104
De transporte de i a j.