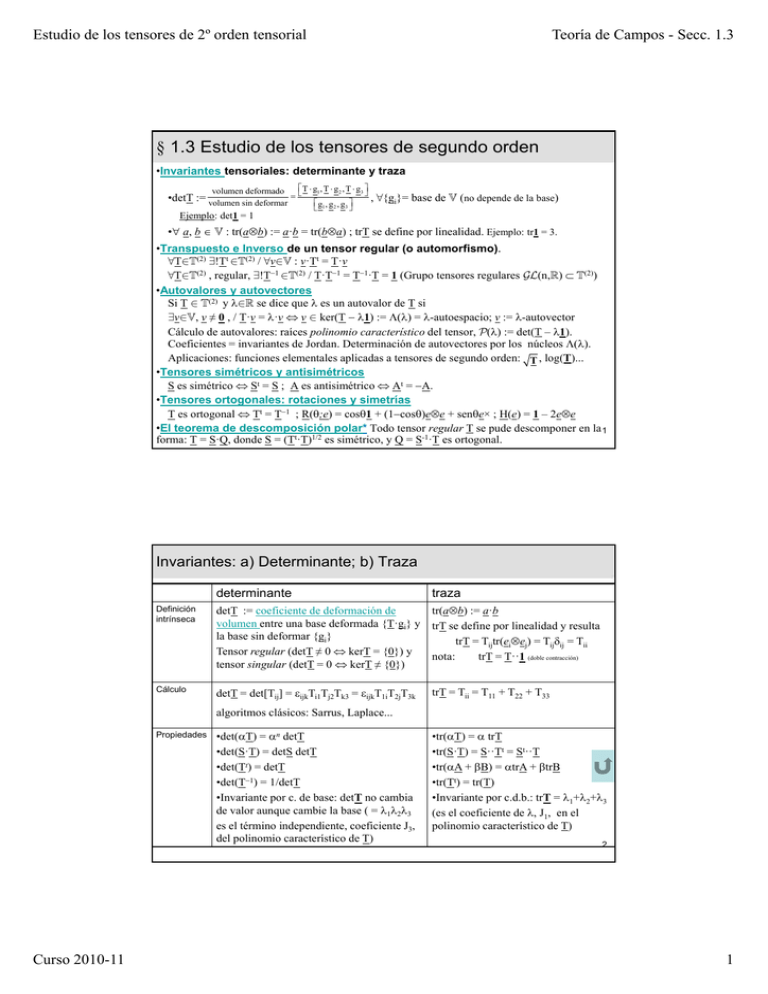
§ 1.3 Estudio de los tensores de segundo orden

Estudio de los tensores de 2º orden tensorial
Teoría de Campos - Secc. 1.3
§ 1.3 Estudio de los tensores de segundo orden
•Invariantes tensoriales: determinante y traza
volumen deformado
•detT := volumen sin deformar 
Ejemplo: det1 = 1
 T  g1 , T  g2 , T  g3 


 g1 , g 2 , g3 


, "{gi}= base de  (no depende de la base)
• a,, b   : tr(ab)
(
) := a·b = tr(ba)
(
) ; trT se define ppor linealidad. Ejemplo:
j p tr1 = 3.
•Transpuesto e Inverso de un tensor regular (o automorfismo).
"TÎ(2) $!Tt Î(2) / "vÎ : v·Tt = T·v
"TÎ(2) , regular, $!T1 Î(2) / T·T1 = T1·T = 1 (Grupo tensores regulares (n,)  (2))
•Autovalores y autovectores
Si T Î (2) y Î se dice que  es un autovalor de T si
$vÎ, v ≠ 0 , / T·v = ·v  v Î ker(T  1) := ) = -autoespacio; v := -autovector
Cálculo de autovalores: raíces polinomio característico del tensor, () := det(T – 1).
Coeficientes = invariantes de Jordan
Jordan. Determinación de autovectores por los núcleos ).
)
Aplicaciones: funciones elementales aplicadas a tensores de segundo orden: T , log(T)...
•Tensores simétricos y antisimétricos
S es simétrico  St = S ; A es antisimétrico  At = A.
•Tensores ortogonales: rotaciones y simetrías
T es ortogonal  Tt = T1 ; R(;e) = cos1 + (1cos)ee + sene× ; H(e) = 1 – 2ee
•El teorema de descomposición polar* Todo tensor regular T se pude descomponer en la 1
forma: T = S·Q, donde S = (Tt·T)1/2 es simétrico, y Q = S-1·T es ortogonal.
Invariantes: a) Determinante; b) Traza
determinante
traza
Definición
intrínseca
detT := coeficiente de deformación de
volumen entre una base deformada {T·gi} y
la base sin deformar {gi}
Tensor regular (detT ≠ 0  kerT = {0}) y
tensor singular (detT = 0  kerT ≠ {0})
tr(ab) := a·b
trT se define por linealidad y resulta
trT = Tijtr(eiej) = Tijij = Tii
nota:
trT = T··1 (doble contracción)
Cálculo
detT = det[Tij] = ijkTi1Tj2Tk3 = ijkT1iT2jT3k
trT = Tii = T11 + T22 + T33
algoritmos clásicos: Sarrus, Laplace...
Propiedades
Curso 2010-11
•det(T) = n detT
•det(S·T)
(
) = detS detT
•det(Tt) = detT
•det(T1) = 1/detT
•Invariante por c. de base: detT no cambia
de valor aunque cambie la base ( = 123
es el término independiente, coeficiente J3,
del polinomio característico de T)
•tr(T) =  trT
•tr(S·T)
(
) = S··Tt = St··T
•tr(A + B) = trA + trB
•tr(Tt) = tr(T)
•Invariante por c.d.b.: trT = 1+2+3
(es el coeficiente de , J1, en el
polinomio característico de T)
2
1
Estudio de los tensores de 2º orden tensorial
c) Tensor traspuesto
Traspuesto T
Definición
Cálculo
Teoría de Campos - Secc. 1.3
d) Tensor inverso de uno
regular
Inverso T1
"TÎ(2) $!Tt / "vÎ :v·Tt = T·v
"TÎ(2), regular, $!T-1 /
Ejemplo: (ab)t = ba
T· T-1 = T-1 ·T = 1
Ejemplo: Si ab :
(1 + ab)1 = 1  ab
S = Tt  Sij = Tji  [Sij] = [Tij]t
Algoritmo de trasposición:
intercambio de filas por columnas
Propiedades
•Idempotencia: (Tt)t = T
•linealidad: (S + T)t = St + Tt
•(S·T)t = Tt · St
•det(Tt) = detT
•(T1)t = (Tt)1 = Tt
[T1ij] = [Tij]1
Algoritmos de inversión (Gauss, Adjunta
traspuesta ÷ determinante,…)
•Idempotencia: (T1)1 = T
•(A)-1 = (1/) A-1
•(S·T)1 = T1 · S1
•det(A1) = 1/detA
•(Tt)1 = (T1)t := T-t
3
Ejemplos y ejercicios de a), b), c) y d)
1. Calcular el traspuesto y el inverso de T = 1 + ab , siendo a = 2i + k , b = 2j
solución:
2. Calcular el determinante y la traza del tensor anterior si b = 2j + k
solución:
3 Probar
3.
P b ((ab)
b)t = ba
b aplicando
li
d lla d
definición
fi i ió iintrínseca
tí
solución:
4. Probar (S·T)1 = T1 · S1
solución:
5. Probar que T T(2) el tensor A = Tt·T es un tensor simétrico; si además T es regular, A es
definido positivo. Misma cuestión para el tensor A* = T·Tt.
solución:
6 Calcular
6.
C l l Wt siendo
i d W = × y  un vector
t dado
d d no nulo.
l
solución:
4
Curso 2010-11
2
Estudio de los tensores de 2º orden tensorial
Teoría de Campos - Secc. 1.3
e) Autoanálisis de un tensor: autovalores y autovectores
•Objetivo: describir geométricamente la acción de un tensor arbitrario T de (2).
•Definiciones
•Dado T(2) si $vÎ, v ≠ 0 y $Î / T·v = ·v, se llaman  = autovalor de T y v = autovector.
•Espectro de T, (T) = {Î /  = autovalor de T}
•El conjunto de autovectores asociados a un mismo autovalor , es el subespacio vectorial
() := (ker(T  l) y se llama -autoespacio o s.v. propio asociado a .
•Cálculos
•(T)  det(T  1) = 0 : ecuación característica de T. O sea:  = autovalor de T   es
raíz de la ec. característica.
• El polinomio característico () = det(T  1) es invariante por c. de b.; sus coeficientes se
llaman invariantes de Jordan de T, denotados Ji(T) y son los escalares: J1(T) = trazaT, J2(T) =
suma menores
su
e o es pp
ppales.
es. de 2º orden,
o de , J3((T)) = de
detT..
•Obs: los autovalores se relacionan con los invariantes de Jordan: detT = 123, trazaT = 1+2+3,
J2(T) = 12+13+23.
• v = -autovector  v Î ker(T  1) := ) = -autoespacio (subespacio vectorial asociado
al autovalor ; es invariante por la acción del tensor: en él T se comporta como una homotecia
de razón ).
•Índice de Jordan de , () := dim(); orden de multiplicidad de  = N(). T diagonalizable
5
 () = ().
Aplicaciones (1): diagonalización de un tensor
•Un tensor T es diagonalizable: si existe una base de  formada por autovectores de T
(autobase o base propia). Porque en tal base T tiene una matriz diagonal:
|
 |
Tˆ ij    T  eˆ1 T  eˆ2
  
|
 |
| 
 1 0


ˆ
 0 2
T  e3


| eˆ   0 0
i
0
0   C 1 ·T hk ·C   Q t ·T hk ·Q 

 3 
de modo que la matriz dada que se tenga de T es semejante a una matriz diagonal:
•Son diagonalizables con certeza los tensores con tres autovalores reales simples
(distintos) y también los tensores simétricos (en este caso la autobase es además
ortogonal y sus unitarios se llaman direcciones principales del tensor)
•Son dudosos los tensores con autovalores reales múltiples. Se estudia si J() = N();
si J() < N() el tensor no es diagonalizable.
•No son diagonalizables sobre  los tensores con autovalores complejos.
•Ventajas de la forma diagonal, en particular si la base de autovectores es ortonormal:
interpretación geométrica de la acción de un tensor: figura siguiente
•Ejemplos de simplificaciones:
•Algunos autoanálisis pueden hacerse por consideraciones geométricas (sin cálculos): 1)
rotación de ángulo  alrededor de un eje e; 2) simetría respecto de un plano {e} (diapos. 8)
6
•A veces la matriz de T permite deducir un autovector: 3) PR1.20: e1 y e2 son autovec. de T.
Curso 2010-11
3
Estudio de los tensores de 2º orden tensorial
Teoría de Campos - Secc. 1.3
Aplicaciones (2): interpretación geométrica de los autovectores y
autovalores
Los autovectores se corresponden con direcciones que se
conservan al actuar el tensor (incluyendo o no el sentido).
La recta generada por el autovector, se conserva tras la
acción del tensor: recta invariante. El tensor sobre una
recta invariante se comporta como una homotecia de
razón
ó ell autovalor.
l
Si se dispone de una base de autovectores, {wi},se puede
calcular gráficamente la imagen de cualquier vector v,
como se indica en la figura: se descompone v en la
autobase, v = v1 + v2; luego, se calculan por homotecias de
T·v

v
w
2
v2
v1
w
1)
1
razones i las imágenes T·v1 y T·v2 ; finalmente T·v = T·v1 + T·v2 , por la linealidad de T .
En dimensión 3, si hay un autovalor doble con índice de Jordan 2, su autoespacio () será un
plano vectorial y en ese plano el tensor T vuelve a comportarse como ina homotecia de razón
el autovalor.
7
Ejemplos / e) Autovalores, autovectores y aplicaciones
•Ejemplo 1: (interpretación geométrica o intrínseca) Aplicando el concepto, determinar los
autovalores y autovectores de
•una rotación R(; e)
•una simetría respecto de un plano {e}
•el tensor unidad 1 (uso de la definición directamente)
una simetría respecto de un eje ({e}) (ejercicio de razonamiento geométrico)
•una
•el tensor 1 + ee (uso de ambos métodos: geométrico-intrínseco y analítico o en
componentes)
•Cálculo gráfico de T·v en términos de autovalores y autovectores de T.
•Observación(¡!):  = 0  (T)  kerT ≠ {0} y entonces (0) = kerT
•Problemas: PR1.11, PR1.13, PR1.14, PR1.16. También, PR1.21, apartado 1).
•Ejemplo 2: Probar que si  = C-1·A·C (matrices semejantes) entonces Âm = C-1·Am·C para
cualquier potencia mÎ
•Ejemplo 3: Calcular
 a

 0
0 

b 
•Ejemplo 4: Calcular la matriz
2
a 0
y deducir el valor de 
 supuesto a, b > 0
0 b
m
a 0
donde m es un entero (ejercicio)


0 b
•Ejemplo 5: Calcular la matriz M =
Curso 2010-11
 2
A , siendo A  
 2
2

1 
8
4
Estudio de los tensores de 2º orden tensorial
Teoría de Campos - Secc. 1.3
f) Tensores simétricos, antisimétricos y ortogonales
•Tensores simétricos y su descomposición espectral
•Definición y caracterización: S es simétrico  St = S  "v : v·S = S·v  "u, v : u·S·v =
v·S·u
•Teorema de descomposición espectral: todo tensor simétrico admite una base ortonormal de
autovectores {êi} y autovalores reales de modo que:
S = 1ê1ê1+2ê2ê2+3ê3ê3
•Aplicaciones:
A li i
signatura
i
de
d una forma
f
cuadrática
d á i y su clasificación;
l ifi ió utilidad
ilid d de
d las
l direcciones
di
i
principales
•Tensores antisimétricos y su vector axial
•Definición y caracterización: A es antisimétrico  At = A  "v : v·A = A·v  "u, v :
u·A·v = v·A·u
•Teorema del vector axial: todo tensor antisimétrico A admite un vector axial  tal que : A =
×. El vector axial   kerA
•Descomposición de tensores en suma parte simétrica ½(T+Tt) y parte antisimétrica, ½(TTt)
•Tensores ortogonales
•Definición y caracterización: Q es ortogonal  Qt = Q1  Q conserva el producto escalar: "
u, v : (Q·u)·(Q·v) = u·v (aplicación conforme, pues Q conservará los ángulos y las distancias)
•Teorema (clasificación): Todo tensor ortogonal tiene determinante 1 ó 1 (no cierto al revés);
los de determinante 1 son rotaciones alrededor de un eje; y los de determinante 1 son
simetrías respecto de un plano o el producto de una rotación por una simetría.
•Los tensores ortogonales forman un subgrupo (n,) del grupo de automorfismo o tensores
9
regulares (n,). Las rotaciones  a su vez son subgrupo de .
Cuadro resumen:
Definición y
ccaracterización
Tensor SIMÉTRICO
S es simétrico 
St =
S
v : v·S = S·v  Sij  = Sij 
Tensor ANTISIMÉTRICO
Tensor ORTOGONAL
A es antisimétrico  At = A 
Q es ortogonal  Qt = Q–1
 v : v·At = A·v 
Q · Q t = Q t ·Q = 1 
  Aij  = –  Aij  '
Propiedad fundamental
En particular: A11 = A22 = A33 = 0
S es un tensor simétrico  S tiene
tres autovalores reales con tres
correspondientes
autovectores
mutuamente ortogonales.
Si 1, 2, 3, son los autovalores de
S, y {ê1,ê2,ê3} son los autovectores
respectivos normalizados, entonces
puede expresar
p
en esa base
S se p
ortonormal mediante la forma
diádica:
S = 1ê1ê1+2ê2ê2+3ê3ê3
(representación espectral de S)
t
1 0 0 
 Qij  · Qij  = 0 1 0
0 0 1
A es antisimétrico    / A·v = Q es ortogonal  conserva el
producto escalar, en el sentido
v, o sea, tal que
siguiente:
u, v : (Q·u)·(Q·v) = u·v
A =  
y en particular Q conserva los
ángulos y los módulos de los
 se llama vector axial de A
vectores que transforme.
A12 A13  Además:
 0


ió
 Aij    A12
Si
0
A 23  Q es ortogonall  Q es una rotación

vectorial R(e;) o Q es una simetría
0 
  A13  A 23
entonces:
-A 23 
 =  A13  es su vector axial.


 -A12 
H(e) o Q es el producto de una
rotación y una simetría.
Además, Q es ortogonal  detQ =
±1, y
Q es una rotación  detQ = 1
(siendo Q ortogonal previamente).
10
Curso 2010-11
5
Estudio de los tensores de 2º orden tensorial
Teoría de Campos - Secc. 1.3
autoanálisis y expresiones reducidas
Autoanálisis y expreesión reducida
Tensor simétrico
S
es
pues
Tensor antisimétrico
Tensor ortogonal
diagonalizable:
la A no es diagonalizable al tener Si Q es una rotación R(e;), Q no
complejos.
Su
representación matricial de S en sus autovalores
representación
matricial
más es diagonalizable y se estudia
autovectores {êi} es la matriz sencilla se obtiene en la base: e = aparte.
3
diagonal:

Ŝij  =  
  




0


 

H(e) Q es
, e1{} (arbitrario), e2 := Si Q es una simetría H(e),
| |
diagonalizable.
e3×e1, resultando:
0
[Âij] = 

0

0
0
0
0

0
•Ejemplo 1: Demostrar que el producto de dos rotaciones es una nueva rotación.
•Ejemplo 2: Probar que el producto de dos simetrías respecto de dos planos 1 y 2 es una rotación e
identificar el eje en términos de dichos planos.
11
g) Rotaciones y simetrías
•Expresión intrínseca de una rotación:
R = R(;e) = cos 1 + (1-cos)ee + sen e×
Aplicaciones:
• es tal que trR = 1+2cos.
•e es el vector axial del tensor e× = 2sen1  (R  R t ) en la dirección del autovector del
autovalor  = 1 que necesariamente tiene la rotación
•Expresión intrínseca de una simetría respecto {e} : H(e) = 1 – 2ee
•e = autovector del autovalor  = 1 que debe tener H = unitario del vector característico del
plano de simetría.
•plano de simetría dado por {e}.
•Ejemplo 2: Apuntes, Simetría respecto de un eje e
12
Curso 2010-11
6
Estudio de los tensores de 2º orden tensorial
Teoría de Campos - Secc. 1.3
   
R·v  OP  OM  MN  NP

OM   e  e ·v (proyección al eje)
M

N
P
P'
e
v
R·v

 dir.:MP 

MP

MN  

  cos MP 
mód.: MP cos 
 cos  1  e  e ·v
 
 dir.: ev ev
ev

NP  

  MP sen 
mód.: MP sen 
v sen 



ev
 MP sen    sen e  v
MP
O

E n co n secu en cia:
R  co s  1  (1  co s  ) e  e  sen  e 
13
M
v
e
O
N
H·v

H·v  ON  v  2  e  e ·v
H  1  2e  e
14
Curso 2010-11
7
Estudio de los tensores de 2º orden tensorial
Teoría de Campos - Secc. 1.3
 23 0 3 
1  23  (T)  i   ( 23 )

 T·i  23 i
[Tij ]   0 3 0   

T· j  3 j
 0 0 3   T
  2  3  (T)  j   (3)
2

15
Curso 2010-11
8