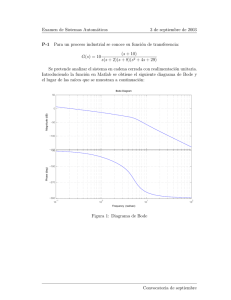
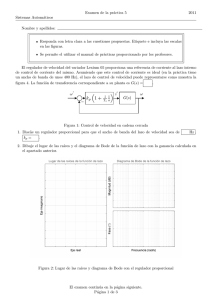
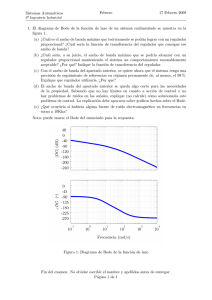
apuntes de sistemas de control

APUNTES DE SISTEMAS
DE CONTROL
R. P. Ñeco
O. Reinoso
N. Garcı́a
Elche, octubre, 2003
R. Aracil
II
Índice general
Índice de Figuras
X
Índice de Tablas
XIX
Prólogo
XXI
I
Análisis de sistemas continuos de control realimentados
1. Introducción
1.1. Sistemas de control. Conceptos básicos . . . . . . . . . . . . . . .
1.1.1. Elementos en un sistema de control . . . . . . . . . . . . .
1.1.2. Control en bucle abierto y bucle cerrado . . . . . . . . . .
1.1.3. Realimentación de sistemas . . . . . . . . . . . . . . . . .
1.1.4. Esquemas tı́picos de control . . . . . . . . . . . . . . . . .
1.2. Comportamiento dinámico de sistemas continuos. Resumen . . .
1.2.1. La Transformada de Laplace . . . . . . . . . . . . . . . .
1.2.2. Función de Transferencia de un sistema . . . . . . . . . .
1.2.3. Respuesta temporal de un sistema continuo . . . . . . . .
1.2.4. Sistemas de primer orden . . . . . . . . . . . . . . . . . .
1.2.5. Sistemas de segundo orden . . . . . . . . . . . . . . . . .
1.2.6. Sistemas de orden superior: Sistema reducido equivalente
1.3. Estudio de la estabilidad de sistemas continuos realimentados . .
1.3.1. Criterio de Routh . . . . . . . . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
4
5
5
7
7
8
9
11
11
12
13
17
18
18
19
2. Análisis en régimen permanente de sistemas continuos realimentados 21
2.1. Respuesta en régimen transitorio y en régimen permanente en el dominio
del tiempo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.2. Error en régimen permanente . . . . . . . . . . . . . . . . . . . . . . . . . 23
iii
IV
ÍNDICE GENERAL
2.3. Señales de entrada normalizadas . . . . . . . . . . . . . . . . . . . . . . .
2.4. Tipo de un sistema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5. Constantes de error en sistemas con realimentación unitaria . . . . . . . .
2.5.1. Error ante una entrada escalón. Error de posición. Constante de
error de posición . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.2. Error ante una entrada rampa. Error de velocidad. Constante de
error de velocidad . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.3. Error ante una entrada parabólica. Error de aceleración. Constante
de error de aceleración . . . . . . . . . . . . . . . . . . . . . . . . .
2.6. Errores en sistemas con realimentación no unitaria . . . . . . . . . . . . .
2.6.1. Transformación en un sistema equivalente con realimentación unitaria
2.6.2. Cálculo del error a partir de la ganancia estática de la realimentación
2.7. Comparación bucle abierto-bucle cerrado . . . . . . . . . . . . . . . . . . .
2.8. Sensibilidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
29
30
3. Técnica del lugar de las raı́ces
3.1. Ecuaciones básicas del lugar de las raı́ces . . . . . . . . . . . . . . . . . .
3.2. Reglas para el trazado del lugar de las raı́ces . . . . . . . . . . . . . . . .
3.2.1. Ejemplos de trazado del lugar de las raı́ces . . . . . . . . . . . . .
3.2.1.1. Ejemplo 1 . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.1.2. Ejemplo 2 . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3. Forma básica del lugar de las raı́ces en sistemas de primer y segundo orden
3.3.1. Sistemas de primer orden . . . . . . . . . . . . . . . . . . . . . . .
3.3.2. Sistemas de segundo orden . . . . . . . . . . . . . . . . . . . . . .
3.3.2.1. Adición de ceros a un sistema de segundo orden simple .
3.3.2.2. Adición de polos a un sistema de segundo orden simple .
3.3.3. Sistemas de fase no mı́nima . . . . . . . . . . . . . . . . . . . . . .
3.4. Contorno de las raı́ces . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
46
48
53
53
55
56
56
59
60
65
65
67
72
4. Análisis dinámico de sistemas continuos en el dominio de la frecuencia
4.1. Respuesta en frecuencia de un sistema . . . . . . . . . . . . . . . . . . . .
4.1.1. Justificación del estudio de la respuesta en frecuencia . . . . . . .
4.1.2. Régimen permanente senoidal . . . . . . . . . . . . . . . . . . . . .
4.2. Diagramas de respuesta en frecuencia . . . . . . . . . . . . . . . . . . . .
4.2.1. Representación de los Diagramas de Bode . . . . . . . . . . . . . .
4.2.2. Diagrama de Nyquist o trazado polar . . . . . . . . . . . . . . . .
4.2.3. Diagrama de Black-Nichols . . . . . . . . . . . . . . . . . . . . . .
4.2.4. Identificación en frecuencia . . . . . . . . . . . . . . . . . . . . . .
4.3. Frecuencia de resonancia . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4. Estabilidad de un sistema realimentado . . . . . . . . . . . . . . . . . . .
73
75
75
76
77
77
87
88
88
91
92
30
31
32
34
34
36
38
40
42
R.P. Ñeco, O. Reinoso, N. Garcı́a, R. Aracil
4.5. Principio del argumento de Cauchy . . . . . . . . . . . . . . . . . . . . . .
4.6. Camino de Nyquist . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7. Criterio de estabilidad de Nyquist . . . . . . . . . . . . . . . . . . . . . .
4.7.1. Ejemplos de aplicación del criterio de Nyquist . . . . . . . . . . . .
4.8. Introducción de polos y ceros adicionales . . . . . . . . . . . . . . . . . . .
4.8.1. Adición de polos reales . . . . . . . . . . . . . . . . . . . . . . . . .
4.8.2. Adición de polos en el origen . . . . . . . . . . . . . . . . . . . . .
4.8.3. Adición de ceros reales . . . . . . . . . . . . . . . . . . . . . . . . .
4.9. Criterio de Nyquist para sistemas de fase mı́nima. Estabilidad relativa . .
4.10. Márgenes de ganancia y de fase . . . . . . . . . . . . . . . . . . . . . . . .
4.11. Estabilidad en los diagramas de Bode . . . . . . . . . . . . . . . . . . . .
4.11.1. Frecuencia de corte y ancho de banda . . . . . . . . . . . . . . . .
4.12. Respuesta en frecuencia en bucle cerrado. Cı́rculos M y N. Diagrama de
Black-Nichols . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.12.1. Sistemas con realimentación unitaria . . . . . . . . . . . . . . . . .
4.12.2. Sistemas con realimentación no unitaria . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
II
Diseño de sistemas continuos de control
V
94
98
101
102
105
105
107
109
109
110
113
115
117
118
121
122
123
5. Consideraciones sobre el diseño y acciones básicas de control
5.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2. Tipos de compensación . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3. Metodologı́as para el diseño de reguladores . . . . . . . . . . . . . . . . .
5.3.1. Especificaciones de funcionamiento . . . . . . . . . . . . . . . . . .
5.4. Condiciones básicas del sistema de control . . . . . . . . . . . . . . . . . .
5.5. Acciones básicas de control . . . . . . . . . . . . . . . . . . . . . . . . . .
5.6. Reguladores de tipo P e I . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.7. Regulador de tipo PD . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.8. Regulador de tipo PI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.9. Regulador PID . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.10. Efectos de las acciones de control integral y diferencial en el comportamiento de un sistema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
125
126
129
130
131
134
134
136
138
141
142
6. Diseño de reguladores PID continuos. Método del lugar de las raı́ces
6.1. Enfoque del lugar de las raı́ces para el diseño de sistemas de control . . .
6.2. Sistema equivalente de orden reducido . . . . . . . . . . . . . . . . . . . .
6.3. Compensación mediante regulador PD . . . . . . . . . . . . . . . . . . . .
6.3.1. Ejemplo introductorio . . . . . . . . . . . . . . . . . . . . . . . . .
6.3.2. Procedimiento de diseño de un regulador PD . . . . . . . . . . . .
147
148
150
151
152
156
145
145
ÍNDICE GENERAL
VI
6.3.3. Criterios para situar el cero de un regulador PD . .
6.4. Compensación mediante regulador PI . . . . . . . . . . . .
6.4.1. Pasos en el diseño de un regulador PI . . . . . . . .
6.5. Compensación mediante un regulador PID . . . . . . . . . .
6.6. Otros métodos de ajuste de reguladores tipo PID . . . . . .
6.6.1. Reglas de Ziegler-Nichols para sintonizar reguladores
6.6.1.1. Primer método . . . . . . . . . . . . . . . .
6.6.1.2. Segundo método . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
160
160
164
165
171
172
173
174
175
7. Diseño de reguladores continuos. Método de respuesta en frecuencia
7.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.1.1. Especificaciones en el dominio de la frecuencia . . . . . . . . . . .
7.1.2. Análisis del diagrama de Bode de un sistema en bucle abierto . . .
7.1.3. Método de la respuesta en frecuencia para la compensación de un
sistema realimentado . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2. Compensación mediante red de adelanto de fase . . . . . . . . . . . . . . .
7.2.1. Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2.2. Limitaciones del control de adelanto de fase . . . . . . . . . . . . .
7.3. Compensación mediante red de retraso de fase . . . . . . . . . . . . . . .
7.3.1. Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.2. Efectos y limitaciones del control de retraso de fase . . . . . . . . .
7.4. Compensación mediante red de atraso-adelanto de fase . . . . . . . . . . .
7.4.1. Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
177
178
179
181
III
. . .
. . .
. . .
. . .
. . .
PID
. . .
. . .
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
181
182
185
188
190
193
195
196
197
200
Análisis de sistemas discretos de control realimentados 203
8. Conceptos de teorı́a de sistemas discretos
8.1. Sistemas controlados por computador. Motivación.
8.2. Sistemas discretos. Secuencias. . . . . . . . . . . .
8.2.1. Propiedades de las secuencias . . . . . . . .
8.2.2. Secuencia de ponderación . . . . . . . . . .
8.3. La transformada Z. . . . . . . . . . . . . . . . . . .
8.3.1. Propiedades de la transformada Z . . . . .
8.3.2. Transformada inversa Z . . . . . . . . . . .
8.3.3. Función de transferencia en Z . . . . . . . .
8.4. Muestreo y reconstrucción de señales . . . . . . . .
8.4.1. Teorema del muestreo . . . . . . . . . . . .
8.5. Sistemas muestreados . . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
205
206
206
207
208
208
209
209
210
211
211
211
214
VII
R.P. Ñeco, O. Reinoso, N. Garcı́a, R. Aracil
9. Estabilidad en sistemas discretos
215
9.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216
9.2. Transformaciones del plano s al plano z . . . . . . . . . . . . . . . . . . . 218
9.2.1. Eje imaginario . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219
9.2.2. Semiplano negativo . . . . . . . . . . . . . . . . . . . . . . . . . . . 219
9.2.3. Región del plano s . . . . . . . . . . . . . . . . . . . . . . . . . . . 221
9.2.4. Rectas de abscisa constante . . . . . . . . . . . . . . . . . . . . . . 222
9.2.5. Recta que pasa por el origen . . . . . . . . . . . . . . . . . . . . . 222
9.2.6. Rectas de ω constante . . . . . . . . . . . . . . . . . . . . . . . . . 223
9.3. Estabilidad en el plano s y en el plano z . . . . . . . . . . . . . . . . . . . 224
9.3.1. Efectos de los polos sobre la estabilidad de un sistema discreto . . 225
9.3.2. Métodos para la determinación de la estabilidad en sistemas discretos227
9.4. Métodos algebraicos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 229
9.4.1. Criterio de Jury . . . . . . . . . . . . . . . . . . . . . . . . . . . . 230
9.4.2. Análisis de estabilidad mediante la transformación bilineal y el
criterio de estabilidad de Routh . . . . . . . . . . . . . . . . . . . . 234
9.5. Consideraciones finales sobre el estudio de estabilidad . . . . . . . . . . . 237
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 237
10.Análisis dinámico de sistemas discretos
239
10.1. Respuesta ante la secuencia impulso . . . . . . . . . . . . . . . . . . . . . 240
10.2. Respuesta ante un escalón unitario . . . . . . . . . . . . . . . . . . . . . . 241
10.3. Sistema reducido equivalente . . . . . . . . . . . . . . . . . . . . . . . . . 243
10.3.1. Eliminación de pares polo-cero . . . . . . . . . . . . . . . . . . . . 245
10.3.2. Eliminación de polos de módulo comparativamente pequeño . . . . 246
10.3.3. Resumen. Reglas para la obtención del sistema reducido equivalente 247
10.4. Sistemas de primer orden . . . . . . . . . . . . . . . . . . . . . . . . . . . 248
10.4.1. Respuesta a la secuencia impulso . . . . . . . . . . . . . . . . . . . 249
10.4.2. Respuesta a la secuencia escalón unitario . . . . . . . . . . . . . . 250
10.4.3. Especificaciones de los sistemas discretos de primer orden . . . . . 253
10.5. Sistemas de segundo orden . . . . . . . . . . . . . . . . . . . . . . . . . . . 254
10.5.1. Sistemas de segundo orden con dos polos reales . . . . . . . . . . . 254
10.5.2. Sistemas de segundo orden con dos polos complejos conjugados . . 255
10.5.3. Caracterı́sticas dinámicas temporales . . . . . . . . . . . . . . . . . 257
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 259
11.Sistemas discretos realimentados
11.1. Errores en régimen permanente . . . . . . . . . . .
11.1.1. Señales discretas de entrada normalizadas .
11.1.2. Tipo de un sistema discreto . . . . . . . . .
11.1.3. Medidas del error en régimen permanente .
11.2. Errores en sistemas con realimentación no unitaria
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
261
262
264
265
265
268
ÍNDICE GENERAL
VIII
11.3. Influencia de las perturbaciones
11.4. Técnica del lugar de las raı́ces .
11.4.1. Reglas de construcción .
Bibliografı́a para ampliar . . . . . .
sobre el error en régimen permanente
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
271
273
275
275
12.Análisis de sistemas discretos en el dominio de la frecuencia
277
12.1. Respuesta en frecuencia de un sistema discreto de control . . . . . . . . . 278
12.2. Representación gráfica de la respuesta en frecuencia de un sistema discreto
de control . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280
12.2.1. Trazado polar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280
12.2.2. Transformación bilineal . . . . . . . . . . . . . . . . . . . . . . . . 281
12.2.3. Diagramas de Bode . . . . . . . . . . . . . . . . . . . . . . . . . . 282
12.3. Análisis de estabilidad en el dominio de la frecuencia. Criterio de Nyquist 283
12.3.1. Criterio de Estabilidad de Nyquist en el plano ω . . . . . . . . . . 285
12.3.2. Ejemplos de aplicación del criterio de Nyquist para sistemas discretos286
12.3.2.1. Ejemplo 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . 286
12.3.2.2. Ejemplo 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . 288
12.4. Estabilidad relativa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
IV
Diseño de sistemas discretos de control
13.Discretización de Reguladores Continuos
13.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.2. Métodos de discretización . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.3. Métodos basados en la aproximación de la evolución temporal . . . . . . .
13.4. Discretización por integración numérica. Aplicación a la discretización del
regulador PID . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.4.1. Acción proporcional . . . . . . . . . . . . . . . . . . . . . . . . . .
13.4.2. Acción integral . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.4.3. Acción diferencial . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.4.4. Regulador proporcional-integral o regulador PI . . . . . . . . . . .
13.4.5. Regulador proporcional-diferencial o regulador PD . . . . . . . . .
13.4.6. Regulador PID digital . . . . . . . . . . . . . . . . . . . . . . . . .
13.5. Discretización por emparejamiento de polos y ceros . . . . . . . . . . . . .
13.6. Configuraciones del regulador PID . . . . . . . . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
293
295
296
300
301
302
304
304
308
310
311
312
314
317
318
IX
R.P. Ñeco, O. Reinoso, N. Garcı́a, R. Aracil
14.Diseño de reguladores PID discretos. Extensión de las técnicas clásicas321
14.1. Diseño de reguladores PID discretos con el método del lugar de las raı́ces 322
14.1.1. Reguladores PD . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323
14.1.2. Reguladores PI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327
14.1.3. Reguladores PID . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329
14.2. Métodos frecuenciales de diseño . . . . . . . . . . . . . . . . . . . . . . . . 330
14.2.1. Reguladores P . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 330
14.2.2. Efecto de la adición de polos y ceros . . . . . . . . . . . . . . . . . 330
14.2.3. Reguladores PI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 332
14.2.4. Reguladores PD . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 339
15.Diseño por sı́ntesis directa I
15.1. Método de Truxal o de sı́ntesis directa . . . . . . . . . . . . . . . . . . .
15.1.1. Condiciones para el diseño de un controlador por sı́ntesis directa
15.1.1.1. Realización fı́sica del controlador . . . . . . . . . . . . .
15.1.1.2. Estabilidad del bucle cerrado . . . . . . . . . . . . . . .
15.1.2. Método de diseño de controladores por sı́ntesis directa . . . . . .
15.2. Método de asignación de polos . . . . . . . . . . . . . . . . . . . . . . .
15.2.1. Eliminación del error en régimen permanente . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
16.Diseño por sı́ntesis directa II.
Controladores de tiempo mı́nimo y tiempo finito
16.1. Controladores de tiempo mı́nimo . . . . . . . . . . . . . . . . . . . . . . .
16.1.1. Consideración del retardo del proceso . . . . . . . . . . . . . . . .
16.1.2. Procesos con ceros de fase no mı́nima y/o polos fuera del cı́rculo
unidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16.1.3. Cálculo del orden de M (z −1 ) . . . . . . . . . . . . . . . . . . . . .
16.1.4. Cálculo de la rapidez de un controlador de tiempo mı́nimo . . . . .
16.1.5. Caso particular: procesos con polos en z = 1 . . . . . . . . . . . . .
16.1.6. Método de diseño de controladores de tiempo mı́nimo . . . . . . .
16.1.6.1. Modos de resolución de los sistemas polinomiales . . . . .
16.1.6.2. Pasos en el diseño de un controlador de tiempo mı́nimo .
16.2. Controladores de tiempo finito . . . . . . . . . . . . . . . . . . . . . . . .
16.2.1. Definición de los controladores de tiempo finito . . . . . . . . . . .
16.2.2. Análisis de los controladores de tiempo finito . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
BIBLIOGRAFÍA
341
342
343
344
346
349
350
353
354
357
358
361
362
363
363
364
366
366
367
367
368
372
373
375
X
ÍNDICE GENERAL
Índice de figuras
1.1. Sistema de control. . . . . . . . . . . . . . . . . . . . . . . .
1.2. Sistema de control en bucle abierto. . . . . . . . . . . . . .
1.3. Sistema de control en bucle cerrado. . . . . . . . . . . . . .
1.4. Sistema de control continuo. . . . . . . . . . . . . . . . . . .
1.5. Sistema continuo y control discreto. . . . . . . . . . . . . .
1.6. Sistema discreto y control discreto. . . . . . . . . . . . . . .
1.7. Respuesta ante impulso de un sistema de primer orden. . .
1.8. Respuesta ante escalón de un sistema de primer orden. . . .
1.9. Respuesta impulsional de un sistema de segundo orden. . .
1.10. Respuesta ante escalón de un sistema de segundo orden. . .
1.11. Respuesta ante una rampa de un sistema de segundo orden.
2.1.
2.2.
2.3.
2.4.
2.5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Error del sistema. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Sistema sin realimentación. . . . . . . . . . . . . . . . . . . . . . . .
Sistema con realimentación unitaria. . . . . . . . . . . . . . . . . . .
Sistema con realimentación no unitaria. . . . . . . . . . . . . . . . .
Sistema con realimentación no unitaria transformado en un sistema
realimentación unitaria. . . . . . . . . . . . . . . . . . . . . . . . . .
2.6. Sistema en bucle abierto (a) y sistema en bucle cerrado (b). . . . . .
2.7. Sistema ejemplo para el cálculo de sensibilidad. . . . . . . . . . . . .
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
6
7
8
8
9
13
14
15
16
17
. . .
. . .
. . .
. . .
con
. . .
. . .
. . .
24
24
25
26
Sistema en bucle cerrado. . . . . . . . . . . . . . . . . . . . . . . . . . . .
Representación en el plano de los polos y ceros del sistema ejemplo. . . .
Sistemas con polos y ceros cancelables. . . . . . . . . . . . . . . . . . . . .
Sistema de cuarto orden. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lugar de las raı́ces para el sistema del ejemplo 1. . . . . . . . . . . . . . .
Lugar de las raı́ces para el sistema del ejemplo 2. . . . . . . . . . . . . . .
Lugar de las raı́ces de un sistema de primer orden, G(s)H(s) = K/(s + 1).
Lugar de las raı́ces de un sistema de primer orden, G(s)H(s) = K(s +
0,5)/(s + 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
xi
35
39
41
46
49
52
53
53
56
57
58
ÍNDICE DE FIGURAS
XII
3.9. Lugar de las raı́ces de un sistema de primer orden, G(s)H(s) = K(s +
1,5)/(s + 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.10. Lugar de las raı́ces de un sistema de segundo orden, G(s)H(s) = K/(s +
1)(s + 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.11. Lugar de las raı́ces de un sistema de segundo orden, G(s)H(s) = K/(s2 +
3s + 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.12. Lugar de las raı́ces de un sistema de segundo orden, G(s)H(s) = K(s +
3)/(s + 1)(s + 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.13. Lugar de las raı́ces de un sistema de segundo orden, G(s)H(s) = K(s +
1,5)/(s + 1)(s + 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.14. Lugar de las raı́ces de un sistema de segundo orden, G(s)H(s) = K(s +
0,5)/(s + 1)(s + 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.15. Lugar de las raı́ces de un sistema de segundo orden, G(s)H(s) = K(s +
2)/(s2 + 3s + 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.16. Lugar de las raı́ces de un sistema de segundo orden, G(s)H(s) = K(s +
0,5)/(s2 + 3s + 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.17. Lugar de las raı́ces del sistema, G(s)H(s) = K/(s + 2)(s + 1)(s + 3). . . .
3.18. Lugar de las raı́ces del sistema, G(s)H(s) = K/(s + 1)(s2 + 3s + 3). . . .
3.19. Lugar de las raı́ces del sistema, G(s)H(s) = K/(s + 2)(s2 + 3s + 3). . . .
3.20. Sistema en bucle cerrado con tres parámetros. . . . . . . . . . . . . . . . .
3.21. Lugar de las raı́ces simple. . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.22. Contorno de las raı́ces para el parámetro T . . . . . . . . . . . . . . . . . .
3.23. Contorno de las raı́ces para el parámetro a. . . . . . . . . . . . . . . . . .
4.1.
4.2.
4.3.
4.4.
4.5.
4.6.
Sistema en bucle abierto al que se le aplica una entrada senoidal. . . . . .
Diagrama de Bode correspondiente al factor constante. . . . . . . . . . . .
Diagrama de Bode correspondiente a un cero en el origen. . . . . . . . . .
Diagrama de Bode correspondiente a un polo en el origen. . . . . . . . . .
Diagrama de Bode asintótico correspondiente a un polo de primer orden. .
Diagrama de Bode real y asintótico correspondiente a un polo de primer
orden. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7. Diagrama de Bode asintótico correspondiente a un polo de segundo orden.
4.8. Sistema en bucle cerrado. . . . . . . . . . . . . . . . . . . . . . . . . . . .
100
. . . . . . . . . . .
4.9. Diagrama de Bode asintótico del sistema G(s) = s(s+1)
4.10. Diagrama de Bode real y asintótico del sistema G(s) =
4.11. Diagrama de Nyquist o traza polar del sistema G(s) =
100
s(s+1) . .
1
0,001s+1 .
1
4.12. Diagrama de Black-Nichols del sistema G(s) = 0,001s+1
.
4.13. Respuesta en frecuencia obtenida experimentalmente. .
4.14. Sistema en bucle cerrado. . . . . . . . . . . . . . . . . .
4.15. Representación del plano s y del plano F . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
58
59
62
62
63
63
64
64
66
66
67
69
70
71
71
77
79
80
81
83
84
85
86
87
. . . . . .
88
. . . . . .
89
.
.
.
.
90
91
93
96
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
XIII
R.P. Ñeco, O. Reinoso, N. Garcı́a, R. Aracil
4.16. Ejemplo de configuración de polos y ceros para el principio del argumento
de Cauchy. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.17. Camino de Nyquist e imagen asociada. . . . . . . . . . . . . . . . . . . . .
4.18. Camino de Nyquist con singularidades en el origen (a) y sobre el eje imaginario (b). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.19. Detalle del tramo IV del camino de Nyquist de la figura 4.18 (a). . . . . .
4.20. Sistema en bucle cerrado del ejemplo 2. . . . . . . . . . . . . . . . . . . .
4.21. Camino origen (izquierda) y camino imagen (derecha) de Nyquist para el
sistema de la figura 4.20. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
K
4.22. Lugar de Nyquist de G (s)H (s) = 1+T
. . . . . . . . . . . . . . . . . . .
1s
4.23. Lugar de Nyquist de la figura 4.22 con un polo adicional. . . . . . . . . .
4.24. Lugar de Nyquist de la figura 4.22 con un polo adicional en el origen,
K
correspondiente al sistema G(s)H(s) = s(1+T
. . . . . . . . . . . . . . .
1 s)
4.25. Lugar de Nyquist de la figura 4.24 con un polo adicional en el origen,
K
. . . . . . . . . . . . . . .
correspondiente al sistema G(s)H(s) = s2 (1+T
1 s)
4.26. Lugar de Nyquist de la figura 4.25 con un polo adicional en el origen,
K
. . . . . . . . . . . . . . .
correspondiente al sistema G(s)H(s) = s3 (1+T
1 s)
4.27. Efecto de la adición de ceros reales. . . . . . . . . . . . . . . . . . . . . . .
4.28. Margen de ganancia y de fase. . . . . . . . . . . . . . . . . . . . . . . . . .
4.29. Sistema en bucle cerrado ejemplo. . . . . . . . . . . . . . . . . . . . . . .
4.30. Diagrama de Nyquist del sistema de la figura 4.29. . . . . . . . . . . . . .
4.31. Márgenes de ganancia y fase sobre el diagrama de Bode. . . . . . . . . . .
4.32. Frecuencia de corte. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.33. Diagrama de Nyquist del sistema ejemplo. . . . . . . . . . . . . . . . . . .
4.34. Diagrama de Bode del sistema ejemplo. . . . . . . . . . . . . . . . . . . .
4.35. Ejemplo de diagrama de Nichols. . . . . . . . . . . . . . . . . . . . . . . .
5.1. Estructura para el control de un proceso. . . . . . . . . . . . . . . . .
5.2. Estructura para el control de un proceso mostrado en la figura 5.1 con
inclusión de un regulador. . . . . . . . . . . . . . . . . . . . . . . . . .
5.3. Ejemplo de compensación en paralelo. . . . . . . . . . . . . . . . . . .
5.4. Ejemplo de compensación por prealimentación. . . . . . . . . . . . . .
5.5. Diseño del regulador por el método de sı́ntesis. . . . . . . . . . . . . .
5.6. Especificaciones en el dominio del tiempo. . . . . . . . . . . . . . . . .
5.7. Especificaciones en el dominio complejo. . . . . . . . . . . . . . . . . .
5.8. Amortiguamiento de un sistema a partir del margen de fase. . . . . . .
5.9. Regulador de tipo P. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.10. Regulador de tipo I. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.11. Regulador de tipo PD. . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.12. Regulador de tipo PI. . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.13. Regulador de tipo PID (ideal). . . . . . . . . . . . . . . . . . . . . . .
. .
la
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
97
99
100
103
104
105
106
107
108
108
109
110
112
113
114
115
116
118
119
121
127
128
129
130
131
132
133
135
137
138
139
142
143
XIV
ÍNDICE DE FIGURAS
6.1. Compensación de un sistema mediante el regulador GR (s). . . . . . . . .
6.2. Situación del polo dominante deseado. El lugar de las raı́ces del sistema
1
no pasa por dicho polo. . . . . . . . . . . . . . . . . . . . .
Gp (s) = s(s+1)
6.3. Cálculo de los ángulos para la aplicación del criterio del argumento. . . .
6.4. El cero del regulador PD se sitúa sobre el polo -1 del sistema. . . . . . . .
6.5. Lugar de las raı́ces del sistema compensado con un regulador PD. . . . . .
1
, junto con la
6.6. Respuesta al escalón unitario del sistema G(s) = s(s+1)
misma respuesta del sistema compensado con el regulador PD GR (s) =
4(s+1)
s+2,83 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.7. Lugar de las raı́ces de un sistema con función de transferencia G(s)H(s) =
K
s(s+a)(s+b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.8. El ángulo ϕR debe ser aportado por el regulador PD. . . . . . . . . . . . .
6.9. Método gráfico para situar el par polo-cero de un regulador PD. . . . . .
6.10. Compensación con regulador PI: el par de polos dominantes se mantiene
aproximadamente en el mismo punto. . . . . . . . . . . . . . . . . . . . .
6.11. Primer criterio para situar el par polo-cero de un regulador PI. . . . . . .
6.12. Segundo criterio para situar el par polo-cero de un regulador PI. . . . . .
1
. . . . . . . . . . . . . . .
6.13. Lugar de las raı́ces del sistema G(s) = (s+1)(s+2)
6.14. Aplicación del criterio del argumento para obtener el ángulo proporcionado
por el regulador PD. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.15. El cero del regulador PD se sitúa en este caso cancelando el segundo polo
del sistema. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.16. Polos y ceros del regulador PID a diseñar. . . . . . . . . . . . . . . . . . .
6.17. Lugar de las raı́ces del sistema compensado con el regulador PD. . . . . .
6.18. Lugar de las raı́ces del sistema compensado con el regulador PID. . . . . .
6.19. Respuesta ante entrada escalón unitario del sistema original, junto con el
sistema compensado con el PD y PID diseñados. . . . . . . . . . . . . . .
6.20. Primer método de Ziegler-Nichols. . . . . . . . . . . . . . . . . . . . . . .
6.21. Sistema con oscilaciones sostenidas con un periodo crı́tico Pcr . . . . . . .
149
153
154
155
156
157
158
159
161
162
164
165
167
168
168
169
170
171
172
173
175
7.1. Compensación de un sistema bajando la curva de ganancia |G(jw)| (regulador PI). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182
7.2. Compensación de un sistema subiendo la curva de ángulo de fase ∠G(jw)
(regulador PD). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183
7.3. Diagram de Bode de la red de adelanto de fase, para distintos valores de α. 184
7.4. Diagrama de Bode del sistema sin compensar, con K = 143,55, calculada
en el paso 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 186
7.5. Cálculo de la frecuencia de cruce de ganancia (paso 5). . . . . . . . . . . . 187
7.6. Diagrama de Bode del regulador calculado GR (s) = 0,33 1+0,1161s
1+0,038s . . . . . 189
7.7. Diagrama de Bode del sistema compensado con el regulador PD. . . . . . 190
XV
R.P. Ñeco, O. Reinoso, N. Garcı́a, R. Aracil
7.8. Respuesta en bucle cerrado al escalón unitario del sistema sin compensar
y el sistema compensado con el regulador PD calculado. . . . . . . . . . . 191
7.9. Diagrama de Bode de la red de retraso de fase. . . . . . . . . . . . . . . . 192
7.10. Diagrama de Bode del sistema con función de transferencia 7.5 con ganancia K = 287,1, calculada en el paso 1 de diseño del regulador PI. . . . . . 194
7.11. Diagrama de Bode del sistema con función de transferencia 7.5 compensado con el regulador PI calculado. . . . . . . . . . . . . . . . . . . . . . . 195
7.12. Respuesta en bucle cerrado al escalón unitario del sistema con función de
transferencia 7.5 sin compensar y compensado con el regulador PI calculado.196
7.13. Diagrama de Bode del sistema sin compensar con K = 19. . . . . . . . . . 198
7.14. Diagrama de Bode del sistema compensado sólo con el regulador PI. . . . 199
7.15. Diagrama de Bode del sistema compensado con el regulador PID diseñado. 201
7.16. Respuesta en bucle cerrado al escalón unitario del sistema sin compensar
y compensado con el regulador PID diseñado. . . . . . . . . . . . . . . . . 201
8.1.
8.2.
8.3.
8.4.
8.5.
Muestreador. . . . . . . . . . . .
Sistema Hı́brido. . . . . . . . . .
Elemento Bloqueador/Retenedor.
Bloqueador de orden cero. . . . .
Bloqueador de orden uno. . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
211
212
212
213
214
9.1. Sistema discreto representado por su función de transferencia en Z. . . . .
9.2. Sistemas discretos con salida acotada para la entrada escalón unitario. . .
9.3. Sistemas discretos con salida no acotada para la entrada escalón unitario
y, por tanto, inestables. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.4. Sistema formado por la suma de dos bloques. . . . . . . . . . . . . . . . .
9.5. Transformación del eje imaginario al plano z. . . . . . . . . . . . . . . . .
9.6. Transformación del semiplano negativo en el plano s en el interior del
cı́rculo unidad en el plano z. . . . . . . . . . . . . . . . . . . . . . . . . . .
9.7. Ejemplo de transformación del plano s al plano z. . . . . . . . . . . . . . .
9.8. Transformación de la región en el plano s dada por la figura 9.7 al plano z.
9.9. Transformación de la recta que pasa por el origen en el plano s al plano z.
z−2
(in9.10. Respuesta discreta al escalón unitario del sistema G1 (z) = (z−1)(z−3)
estable). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
z−2
9.11. Respuesta discreta al escalón unitario del sistema G2 (z) = (z−0,5)(z+0,7)
(estable). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.12. Respuesta discreta al escalón unitario del sistema G3 (z) = z2z−2
+z+2 (inestable). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.13. Respuesta al escalón unitario del sistema G4 (z) = 2z2z−2
+z+1 (estable). . . .
216
217
10.1. Respuesta a un escalón unitario del sistema
.
.
.
.
.
.
.
.
.
.
Y (z)
R(z)
.
.
.
.
.
.
.
.
.
.
=
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0,5z−0,25
z 2 −1,5z+0,75 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
217
218
220
220
221
222
223
229
230
231
232
. . . . . 244
XVI
ÍNDICE DE FIGURAS
10.2. Secuencia de ponderación para un sistema de primer orden con función de
bz
transferencia G(z) = z−a
, cuando a > 0. . . . . . . . . . . . . . . . . . . .
10.3. Secuencia de ponderación para un sistema de primer orden con función de
bz
transferencia G(z) = z−a
, cuando −1 < a < 0 (sistema estable). . . . . . .
10.4. Secuencia de ponderación para un sistema de primer orden con función de
bz
transferencia G(z) = z−a
, cuando a < −1 (sistema inestable). . . . . . . .
10.5. Respuesta al escalón unitario de un sistema de primer orden con función
bz
de transferencia G(z) = z−a
, (a) cuando a > 0; y (b) cuando a < 0. . . . .
249
250
251
252
0,3z −2
1−1,5z −1 +0,7z −2 .
. . . . . . . 256
10.6. Secuencia de ponderación del sistema G(z) =
10.7. Polos de un sistema de segundo orden. Situación de p − 1. . . . . . . . . . 257
−2
10.8. Respuesta al escalón unitario del sistema G(z) = 1−1,5z0,3z
−1 +0,7z −2 . . . . . . 258
11.1. Sistema discreto de control con realimentación unitaria. . . . . . . . . . . 262
11.2. Sistema equivalente simplificado al de la figura 11.1. . . . . . . . . . . . . 263
11.3. Sistema discreto realimentado con realimentación constante h no unitaria. 268
11.4. Sistema discreto realimentado con realimentación constante h no unitaria,
equivalente al sistema representado en la figura 11.3. . . . . . . . . . . . . 269
11.5. Sistema discreto realimentado con dinámica H(s) en la realimentación
(H(s) no constante). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
11.6. Sistema discreto realimentado equivalente al representado en la figura 11.5. 271
11.7. Sistema discreto realimentado con perturbación. . . . . . . . . . . . . . . 272
12.1. Conjunto bloqueador-proceso-muestreador. . . . . . . . . . . . . . . . . .
12.2. Ejemplo de trazado polar. . . . . . . . . . . . . . . . . . . . . . . . . . . .
12.3. Método gráfico de cálculo de la respuesta en frecuencia de un sistema
muestreado a partir de la respuesta en frecuencia del sistema continuo. . .
12.4. Diagramas que muestran las correspondencias del plano s con el plano z y
del plano z con el plano ω. . . . . . . . . . . . . . . . . . . . . . . . . . . .
12.5. Sistema discreto realimentado para el análisis de estabilidad. . . . . . . .
12.6. Trayectoria para el análisis de estabilidad en el plano z. . . . . . . . . . .
12.7. Sistema muestreado para el ejemplo 1. . . . . . . . . . . . . . . . . . . . .
12.8. Imagen del camino de Nyquist de la figura 12.7 para el ejemplo 1. . . . .
12.9. Sistema muestreado para el ejemplo 2 de análisis de estabilidad. . . . . .
12.10.Camino de Nyquist del ejemplo 2. . . . . . . . . . . . . . . . . . . . . . .
12.11.Imagen del camino de Nyquist del ejemplo 2. . . . . . . . . . . . . . . . .
12.12.Margen de fase γ y margen de ganancia KG de un sistema discreto. . . .
13.1. Sistema de control con controlador continuo frente a sistema
con controlador discreto. . . . . . . . . . . . . . . . . . . . . .
13.2. Sistema discreto de control con realimentación unitaria. . . .
13.3. Discretización del sistema continuo (a) por equivalencia con
muestreado (b). . . . . . . . . . . . . . . . . . . . . . . . . . .
278
281
282
283
284
285
286
287
288
289
290
291
de control
. . . . . . . 297
. . . . . . . 298
el sistema
. . . . . . . 299
XVII
R.P. Ñeco, O. Reinoso, N. Garcı́a, R. Aracil
13.4. Equivalencia entre el sistema continuo (a) y el sistema muestreado (b) en
bucle abierto. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 300
13.5. Respuesta al escalón unitario del sistema continuo GR (s) = 25 s+1
s+5 y su
−1
25−23z
aproximación discreta GR (z) = 1−0,6065z
−1 , con periodo de muestreo T =
0,1 seg y bloqueador de orden cero. . . . . . . . . . . . . . . . . . . . . . .
13.6. Regulador PID continuo. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.7. Método de los rectángulos para la aproximación de la acción integral. . .
13.8. Método de los trapecios para la aproximación de la acción integral. . . . .
13.9. Respuesta ante un escalón unitario de la acción integral I(z) dada por la
aproximación de los trapecios. . . . . . . . . . . . . . . . . . . . . . . . . .
13.10.Regulador PID en paralelo. . . . . . . . . . . . . . . . . . . . . . . . . . .
13.11.Configuración del regulador PID con acciones divididas entre la señal de
error y la de realimentación. . . . . . . . . . . . . . . . . . . . . . . . . . .
13.12.Configuración del regulador PID equivalente a la de la figura 13.11. . . . .
14.1. Polo dominante del sistema. . . . . . . . . . . . . . . . . . . . . . . . . . .
14.2. Aplicación del criterio del módulo y del argumento. . . . . . . . . . . . . .
14.3. Sistema G(z) regulado por GR (z). . . . . . . . . . . . . . . . . . . . . . .
5
. . . . . . . . . . . . .
14.4. Lugar de las raı́ces del sistema G(z) = (z−0,7)(z−0,9)
14.5. Cálculo de los ángulos correspondientes a los ceros y polos del sistema
ejemplo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14.6. Disminución del margen de fase de γ1 a γ2 como consecuencia de la acción
de un regulador P. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14.7. Cálculo del módulo y argumento de G(w)
= ejwT − c · G(w). . . . . . . .
G(w)
. . . . . . . . . . . . .
14.8. Cálculo del módulo y argumento de G(w)
= jwT
e
−p
14.9. Sistema regulado con un regulador PI. . . . . . . . . . . . . . . .
14.10.Sistema discreto equivalente regulado con un regulador PI. . . .
14.11.El cero c del regulador PI se añade cercano al polo p = 1. . . . .
14.12.Sistema regulado con un regulador PD. . . . . . . . . . . . . . .
14.13.El cero c del regulador PD se coloca tal que el desfase adicional
frecuencia wg sea ϕ. . . . . . . . . . . . . . . . . . . . . . . . . .
14.14.Aumento del margen de fase con un regulador PD. . . . . . . . .
. . .
. . .
. . .
. . .
para
. . .
. . .
. .
. .
. .
. .
la
. .
. .
303
304
305
306
308
313
317
318
323
325
325
326
326
331
332
333
334
334
335
336
338
339
15.1. El controlador de sı́ntesis directa situado en serie con el proceso “cancela”
la dinámica de GP (z). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 343
15.2. Bucle cerrado discreto de control. . . . . . . . . . . . . . . . . . . . . . . . 351
16.1. Situación de la función de transferencia del error, E(z −1 ), en el bucle
cerrado discreto. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 359
100
con el controla16.2. Respuesta al escalón unitario del proceso G(s) = s2 +3s+2
dor de tiempo mı́nimo, presentando oscilaciones ocultas. . . . . . . . . . . 368
XVIII
ÍNDICE DE FIGURAS
16.3. La acción de control tras el bloqueador de orden cero con el controlador
de tiempo mı́nimo diseñado. . . . . . . . . . . . . . . . . . . . . . . . . . . 369
16.4. Respuesta al escalón unitario y acción de control con oscilaciones ocultas. 370
Índice de tablas
1.1. Transformadas de Laplace de funciones tı́picas. . . . . . . . . . . . . . . .
1.2. Tabla de Routh. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
19
2.1. Constantes de error y errores en régimen permanente en función del tipo
del sistema. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
3.1. Tabla de Routh para el sistema del ejemplo 1. . . . . . . . . . . . . . . . .
55
6.1. Reglas de sintonización para el primer método de Ziegler-Nichols. . . . . . 174
6.2. Reglas de sintonización para el segundo método de Ziegler-Nichols. . . . . 175
8.1. Transformada Z de secuencias básicas. . . . . . . . . . . . . . . . . . . . . 209
8.2. Propiedades de la transformada Z. . . . . . . . . . . . . . . . . . . . . . . 209
9.1. Forma general de la tabla de estabilidad de Jury. . . . . . . . . . . . . . . 233
9.2. Tabla de estabilidad de Jury para el polinomio z 3 + 0,4z 2 + (0,47 + b)z + 0,13.233
9.3. Tabla de Routh del sistema ejemplo. . . . . . . . . . . . . . . . . . . . . . 237
11.1. Valor de los errores en régimen permanente en función del tipo del sistema
discreto. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268
12.1. Valores de BG(z) para el tramo I. . . . . . . . . . . . . . . . . . . . . . . 289
16.1. Eliminación del error en régimen permanente en un tiempo mı́nimo para
procesos con retardo 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 361
xix
XX
ÍNDICE DE TABLAS
Prólogo
El libro que ahora presentamos nace con la pretensión de ofrecer una introducción
a la teorı́a clásica de control continuo y discreto de sistemas. Puede ser útil como libro
de texto en asignaturas de distintas ingenierı́as e ingenierı́as técnicas (industrial, telecomunicaciones, informática, etc.), aunque también puede usarse para introducirse en
el apasionante tema del control automático a ingenieros en ejercicio. Se requiere haber
seguido un curso básico sobre Teorı́a de Sistemas (continuos y discretos) previamente a
la lectura del libro. No obstante, en las partes I y III del libro se da un breve repaso sobre
el análisis de sistemas continuos y discretos, respectivamente.
Existen excelentes textos sobre teorı́a de Sistemas de Control, algunos de ellos muy
clásicos, como los de los profesores Ogata y Kuo que se mencionan en la bibliografı́a tanto
desde el punto de vista discreto como continuo. Asimismo es necesario citar dos textos
clásicos que nos han servido a muchos para introducirnos en la Teorı́a de Sistemas y
Control como son los realizados por los profesores Puente, Aracil y Jiménez en la Universidad Politécnica de Madrid. De esta forma, este libro pretende ser un compendio de lo
expuesto en estos textos clásicos adaptado a los planes de estudio actualmente vigentes
en las escuelas de ingenierı́a de las universidades españolas de forma que los alumnos
puedan seguir perfectamente los diferentes temas expuestos. Este compendio es fruto de
la experiencia docente de los autores que imparten asignaturas sobre Sistemas de Control y Regulación Automática en la Universidad Politécnica de Madrid y la Universidad
Miguel Hernández de Elche desde hace varios años.
En cuanto al contenido del libro, se ha dividido la materia tratada en cuatro partes:
La parte I se dedica al análisis de sistemas continuos realimentados, centrándose en
el análisis en régimen permanente, descripción de la técnica del lugar de las raı́ces
y análisis en el dominio de la frecuencia.
En la parte II se estudian las técnicas clásicas de diseño de sistemas continuos de
control, tanto en el dominio temporal como en el dominio frecuencial. Previamente
xxi
se realizan consideraciones generales sobre el diseño y se describen las acciones
básicas de control.
La parte III se dedica a las técnicas de análisis de sistemas discretos realimentados.
Después de dar un repaso a la teorı́a básica y herramientas matemáticas sobre
sistemas discretos, se pasa a estudiar la estabilidad, análisis dinámico y en régimen
permanente de sistemas discretos realimentados. También se hace una extensión
al caso discreto del análisis en frecuencia estudiado en la parte I para sistemas
continuos.
En la parte IV se describen las técnicas de diseño de sistemas discretos de control.
Los dos primeros capı́tulos de esta parte están dedicados a las técnicas clásicas de
diseño (discretización de controladores continuos y extensión de las técnicas estudiadas para sistemas continuos). En los dos últimos capı́tulos se describen técnicas
especı́ficas de diseño de controladores discretos (por asignación de polos y por sı́ntesis directa, particularizando para el caso de sistemas de tiempo mı́nimo y tiempo
finito).
Al final de todos los capı́tulos se incluyen comentarios sobre bibliografı́a que pueden ser útiles para ampliar algunos aspectos de la materia tratada. Consideramos que
siempre que se estudia una materia es deseable consultar otras fuentes de información
que permitan ahondar en los temas tratados. Por este motivo se ha incluido al final de
cada capı́tulo estas pequeñas referencias bibliográficas que consideramos interesantes de
consultar para ampliar su contenido de forma que le sea más fácil al lector acudir a estas
referencias. Especialmente interesantes son las referencias a libros de problemas resueltos
y propuestos.
Los autores desean reconocer la colaboración prestada por nuestros compañeros del
Área de Ingenierı́a de Sistemas y Automática de la Universidad Miguel Hernández de
Elche durante los primeros años de puesta en marcha de las asignaturas en las que se ha
impartido la materia tratada en este libro.
Los autores,
Profesores
Ramón P. Ñeco
Oscar Reinoso
Nicolás M. Garcı́a
Rafael Aracil
xxii
Parte I
ANÁLISIS DE SISTEMAS
CONTINUOS DE CONTROL
REALIMENTADOS
1
CAPÍTULO 1
INTRODUCCIÓN
Índice
1.1. Sistemas de control. Conceptos básicos . . . . . . . . . . . .
1.1.1. Elementos en un sistema de control . . . . . . . . . . . . . . .
1.1.2. Control en bucle abierto y bucle cerrado . . . . . . . . . . . .
1.1.3. Realimentación de sistemas . . . . . . . . . . . . . . . . . . .
1.1.4. Esquemas tı́picos de control . . . . . . . . . . . . . . . . . . .
1.2. Comportamiento dinámico de sistemas continuos. Resumen
1.2.1. La Transformada de Laplace . . . . . . . . . . . . . . . . . .
1.2.2. Función de Transferencia de un sistema . . . . . . . . . . . .
1.2.3. Respuesta temporal de un sistema continuo . . . . . . . . . .
1.2.4. Sistemas de primer orden . . . . . . . . . . . . . . . . . . . .
1.2.5. Sistemas de segundo orden . . . . . . . . . . . . . . . . . . .
1.2.6. Sistemas de orden superior: Sistema reducido equivalente . .
1.3. Estudio de la estabilidad de sistemas continuos realimentados
1.3.1. Criterio de Routh . . . . . . . . . . . . . . . . . . . . . . . .
Bibliografı́a para ampliar . . . . . . . . . . . . . . . . . . . . . . . .
4
5
5
7
7
8
9
11
11
12
13
17
18
18
19
Para poder llevar a cabo un estudio adecuado de los sistemas de control es preciso
un repaso de los conceptos fundamentales alcanzados en un curso de teorı́a de sistemas.
De esta forma, en este capı́tulo se presentan los resultados básicos y fundamentales del
comportamiento de sistemas continuos. Se comenzará introduciendo los conceptos básicos
3
4
Introducción
ası́ como los elementos que integran un sistema de control junto con el concepto de
realimentación haciendo especial hincapié en sus caracterı́sticas frente al control en
bucle abierto. En un posterior apartado se revisan las propiedades de la transformada
de Laplace que posibilitan el estudio de los sistemas continuos. Asimismo se repasa la
respuesta temporal de los sistemas de primer y segundo orden ası́ como sus parámetros
caracterı́sticos. Por último se presenta el criterio de Routh para analizar la estabilidad
de un sistema continuo. Este primer capı́tulo sirve como base para el posterior desarrollo
de los capı́tulos dedicados a los sistemas realimentados.
1.1.
Sistemas de control. Conceptos básicos
Quizás una de las primeras cuestiones que nos deberı́amos plantear antes de estudiar
los sistemas de control consistirı́a en intentar responder la pregunta ¿qué es el control?.
Serı́a difı́cil responder de una forma exacta a esta pregunta, pero todos tenemos una
idea más o menos clara de la respuesta. Ası́ encontramos en la vida cotidiana numerosos
ejemplos donde podemos observar que existe control de algún sistema. El ejemplo más
cercano lo encontramos en las viviendas donde observamos la existencia de un mecanismo
que permite regular la temperatura de las viviendas. Basándonos en este ejemplo podemos
entender cómo el mecanismo actúa sobre un sistema (caldera, etc.) para que la vivienda
alcance una mayor o menor temperatura (señal de salida) en relación con la temperatura
que nosotros deseemos (señal de referencia). Hoy en dı́a, casi todas las actividades en las
que se desarrolla el ser humano aparece involucrado de alguna u otra forma un sistema
de control.
De esta forma podrı́amos considerar en un sentido lo más amplio posible un sistema
de control como aquel sistema que ante unos objetivos determinados responde con una
serie de actuaciones (figura 1.1).
Objetivos
Sistema de control
Actuaciones
Figura 1.1: Sistema de control.
En el presente libro se van a considerar sistemas tanto de tiempo continuo como de
tiempo discreto, lineales e invariantes con el tiempo. Recordemos que un sistema continuo
se dice que es lineal si se puede aplicar al mismo el principio de superposición. De igual
forma, cuando los parámetros del sistema son estacionarios con respecto al tiempo el
sistema se denomina invariante con el tiempo. Ası́ pues, dentro de la teorı́a de sistemas
de control, el ámbito de este libro queda restringido a considerar sistemas (tanto continuos
como discretos) lineales e invariantes con el tiempo.
R.P. Ñeco, O. Reinoso, N. Garcı́a, R. Aracil
1.1.1.
5
Elementos en un sistema de control
En todo sistema de control aparecen claramente diferenciados una serie de elementos
caracterı́sticos al mismo que es necesario clarificar:
Variable a controlar. Generalmente se le conoce como señal de salida. Constituye la
señal que deseamos que adquiera unos valores determinados. En el ejemplo anteriormente descrito la señal de salida o variable a controlar serı́a la temperatura
ambiente de la vivienda o de una habitación determinada.
Planta o Sistema. La planta o sistema constituye el conjunto de elementos que realizan
una determinada función. En el ejemplo propuesto la planta o sistema lo constituirı́a
toda la vivienda en su conjunto. El sistema estarı́a determinado por las relaciones
de transmisión de calor en la misma con las aportaciones y fugas que presentase en
función de sus caracterı́sticas.
Sensor. El sensor es el elemento que permite captar el valor de la variable a controlar en
determinados instantes de tiempo. En el caso propuesto consistirı́a en el elemento
que permitirı́a conocer la temperatura de la vivienda en determinados momentos.
Señal de referencia. Es la señal consigna o valor que deseamos que adquiera la señal
de salida (objetivo de control). En el ejemplo indicarı́a la temperatura que deseamos
que tenga la vivienda a lo largo de toda la jornada.
Actuador. El actuador es el elemento que actúa sobre el sistema modificando de esta
forma la señal de salida. En el caso de un sistema de calefacción consistirı́a en la
caldera que permite aportar mayor o menor cantidad de calor sobre el sistema o
planta (vivienda) a regular.
Controlador. El controlador o regulador es el elemento que comanda al actuador en
función del objetivo de control. En el ejemplo planteado anteriormente, el regulador
tendrı́a como misión decidir cuál debe ser la aportación de la caldera en todo
instante para mantener el objetivo de control (temperatura de la vivienda).
Todos estos elementos aparecen de alguna u otra forma en casi todo sistema de control.
Identificar y estudiar cada uno de ellos de una forma correcta resulta esencial para poder
diseñar un controlador que permita alcanzar el objetivo de control deseado en todo
instante.
1.1.2.
Control en bucle abierto y bucle cerrado
Cuando se desea mantener un objetivo de control determinado en un sistema dos son
los esquemas de control que se pueden considerar: sistemas de control en bucle abierto y
sistemas de control en bucle cerrado.
6
Introducción
Un sistema de control en bucle abierto es aquel en el que la señal de salida no influye
sobre la acción de control. De esta forma el controlador o regulador no tiene en cuenta
el valor de la señal de salida, ni se compara ésta con la señal de referencia para decidir
la actuación en todo instante sobre el sistema. El caso más tı́pico de un sistema de
control en bucle abierto lo constituye la lavadora eléctrica donde el sistema de control
va modificando el tiempo, la temperatura de lavado, etc. en función de la indicación
del usuario y no en función del nivel de lavado de la ropa (que constituirı́a el objetivo
de control). De esta forma el usuario decide el programa que desea realizar (señal de
referencia), y el controlador actúa sobre los diferentes mecanismos del sistema (lavadora)
de forma que realiza una serie de actuaciones sin tener en cuenta la señal de salida. En
la figura 1.2 se pueden observar las señales involucradas en un control en lazo abierto.
Entrada de
referencia
Controlador
control u
Sistema a controlar
Variable
controlada
Figura 1.2: Sistema de control en bucle abierto.
Evidentemente los sistemas de control en bucle abierto funcionarán razonablemente
bien siempre y cuando hayan sido perfectamente estudiados y no exista ninguna alteración
sobre el sistema. Si el fabricante ha estudiado perfectamente cuál debe ser el proceso de
lavado para la ropa de unas caracterı́sticas determinadas y no se altera en modo alguno el
proceso, el objetivo final quedará perfectamente alcanzado. Sin embargo, en el momento
en que se altere alguna de las caracterı́sticas del proceso (cantidad de ropa, temperatura
del agua, suciedad de la ropa, etc.) por cualquier motivo, el objetivo de control puede no
satisfacerse.
Por el contrario, en los sistemas de control en bucle cerrado existe una realimentación
de la señal de salida o variable a controlar. En este tipo de sistemas se compara la
variable a controlar con la señal de referencia de forma que en función de esta diferencia
entre una y otra, el controlador modifica la acción de control sobre los actuadores de la
planta o sistema. En la figura 1.3 aparece representado un esquema tı́pico de un sistema
controlado en bucle cerrado.
En el sistema de control en bucle cerrado ya no afecta tanto las variaciones en cada
una de las caracterı́sticas del proceso (cantidad de ropa, temperatura, etc.) ya que el
controlador debe actuar en todo instante en función de la diferencia entre la señal a
controlar (limpieza de la ropa) y la señal de referencia (por ejemplo blancura deseada).
Es necesario comentar que si se conociese perfectamente un sistema y no pudiese
alterarse de ninguna forma las caracterı́sticas del mismo (tanto internas como externas),
es más aconsejable utilizar un sistema de control en lazo abierto pues serı́an más sencillos
y económicos. Los sistemas de control en lazo cerrado presentan ventajas cuando se
pueden producir perturbaciones sobre el sistema o bien variaciones impredecibles en
7
R.P. Ñeco, O. Reinoso, N. Garcı́a, R. Aracil
Entrada de
referencia +
-
error
controlador
Sistema a
controlar
Variable
controlada
Figura 1.3: Sistema de control en bucle cerrado.
alguna de las caracterı́sticas del mismo.
1.1.3.
Realimentación de sistemas
En el apartado previo se ha establecido la diferencia entre los sistemas de control
en bucle abierto y los sistemas de control en bucle cerrado. Como quedó establecido, en
estos últimos se compara la señal de salida (o variable que se desea controlar) obtenida
en la mayor parte de las ocasiones a través de un conjunto de sensores, con una señal de
referencia. Este efecto se conoce como realimentación. El efecto inmediato que persigue
esta realimentación es reducir el error entre la señal de salida y la señal de referencia
actuando en consecuencia.
Pero no sólo la realimentación tiene por cometido reducir el error entre la señal de
salida y la señal de referencia de un sistema. La realimentación también produce efectos
sobre la ganancia global del sistema (puede tanto aumentar como disminuir en función
de la realimentación), la estabilidad (un sistema inicialmente estable puede pasar a ser
inestable o a la inversa en función de la realimentación), ası́ como sobre las perturbaciones
posibles que se presenten sobre el mismo (puede reducir el efecto de las perturbaciones
que se originan sobre el sistema). Por lo tanto, la realimentación es un elemento clave
muy a tener en cuenta en el estudio de los sistemas de control ya que puede modificar
considerablemente los resultados producidos por éstos.
1.1.4.
Esquemas tı́picos de control
El esquema tı́pico de control continuo de un sistema en bucle cerrado aparece reflejado
en la figura 1.4. En el mismo aparecen los principales elementos que aparecen en todo
sistema de control: el controlador, los actuadores, la planta o sistema continuo a controlar
y los elementos de realimentación.
Con la aparición de los computadores y los microcontroladores, el uso de controladores digitales ha venido incrementándose en los últimos años. Cuando se desea controlar
sistemas continuos mediante un control de tipo discreto el diagrama de bloques a considerar varı́a ligeramente (Figura 1.5). El controlador en este caso es discreto y como
tal actúa sobre una señal discreta generando una señal discreta a la salida. Esta señal
8
Introducción
R(s) +
å(s)
r(t)
å(t)
-
GR(s)
G(s)
Planta
Y(s)
y(t)
H(s)
Figura 1.4: Sistema de control continuo.
discreta se convierte en una señal continua mediante un convertidor digital/analógico
que en teorı́a de sistemas se denomina bloqueador o retenedor. Dado que el sistema es de
tipo continuo genera a la salida una señal continua. Será necesario por lo tanto, tras la
lectura de esta señal continua por parte de los sensores adecuados, utilizar un convertidor
analógico/digital (muestreador) para poder comparar esta señal con la de referencia y
utilizar la diferencia como entrada al controlador digital.
U(z) +
E(z)
-
GR(z)
B(s)
G(s)
Y(z)
Y(s)
T
T
Figura 1.5: Sistema continuo y control discreto.
Finalmente si el sistema a controlar es de tipo discreto la utilización de un regulador
o controlador discreto es totalmente inmediata (ver Figura 1.6).
1.2.
Comportamiento dinámico de sistemas continuos.
Resumen
En esta sección se repasarán los conceptos fundamentales de los sistemas continuos.
No es nuestro propósito analizar todas las propiedades de los mismos (fuera del ámbito del
presente libro), sino más bien recordar las herramientas y caracterı́sticas fundamentales
de los sistemas continuos que se emplearán para el estudio, análisis y diseño de los
sistemas de control.