Page 1 1.3.3 Valores y funciones propias de un operador y sus
Anuncio

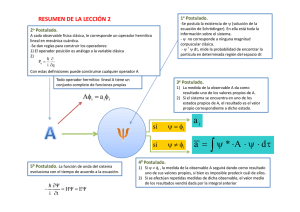
1.3.3 Valores y funciones propias de un operador y sus significativos físicos. "Cuantización" Las fórmulas de la sección anterior permiten calcular los valores esperados de la observable L y del cuadrado de incertidumbre L2 pero no dicen nada sobre el resultado de medición de la observable en cada experimento individual. Para establecer los posibles valores de la observable en las mediciones individuales busquemos los estados con las funciones de onda L en los cuales la observable puede tener un solo valor L. En este tipo de estados el cuadrado de la incertidumbre debe ser igual a cero L2 0 . De esta manera para estos estados L2 L Lˆ2 L L r, t * Lˆ2 L r, t dr Lˆ L dr 0 2 (1) El módulo de un número complejo puede ser igual a cero solo cuando este número es cero, i.e. Lˆ L 0 Según la definición Lˆ Lˆ L . Además para los estados sin incertidumbres, que estamos buscando L L . Por eso (2) (3) Lˆ L L L Este resultado significa que el valor de una observable se puede medir exactamente si el sistema se encuentra en uno de los estados dados por función de onda coincidente con una de las funciones propias del operador asociado a esta observable. Ya que el operador es lineal, esta ecuación para la función de onda L también es lineal y su solución corresponde a un estado en el cual el número L encontrado al resolver la ecuación (3) presenta el único posible valor L de la observable en este estado. En la mayoría de los casos el operador L̂ es diferencial y por esta razón la ecuación (3) presenta una ecuación diferencial lineal. De la teoría de ecuaciones diferenciales se conoce que el problema (3) (llamado el problema de las funciones y valores propias) tiene solucio nes notriviales (no-ceros) solamente cuando esta está complementada por las condiciones adicionales de la frontera (el Problema de SturmLiouvillle, por ejemplo). Sin embargo, incluso cuando las condiciones de frontera están dadas la ecuación diferencial (3) tiene soluciones no triviales solo para algunos valores L1, L2, L3 , , Ln del parámetro L. Las soluciones correspondientes 1, 2, 3 , , n se las funciones propias y los parámetros L1, L2, L3 , , Ln para los cuales las soluciones existen se llamen los valores propios. Un ejemplo más conocido de un problema de esto tipo es el problema de vibración de una cuerda de la longitud a con dos extremos fijos. La ecuación clásica de del movimiento para este caso es: d 2u x k 2u x 0; u 0 u a 0 (4) dx Aquí u x es el desplazamiento del elemento de la cuerda desde la posición de equilibrio y a la longitud de la cuerda. El problema (4) 2 coincide con el problema de valores y funciones propias (3) si ponemos L̂ d 2 dx 2 y L k 2 . Las funciones y valores propios del problema (4) son bien conocidos un x sin nx a ; Ln kn2 2n2 a 2 ; n 1,2,4, . En mecánica cuántica en la mayoría de los casos la función de onda debe estar definida en todo del espacio, por ejemplo en 3D la función x, y, z para x , y , z . Por esta razón a veces las condiciones de frontera en una forma tan directa como para problemas de mecánica Clásica. Sin embargo, se puede demostrar, que la ley de conservación del número de partículas conduce a unas restricciones naturales sobre la función de onda que a veces pueden reemplazar las condiciones de frontera. El requisito de conservación del número de las partículas que es equivalente a la condición de que la probabilidad de encontrar cada partícula en algún punto del espacio debe ser independiente del tiempo, es decir d (5) L r, t * L r, t dr 0 dt Para que se cumpla condición (5) la función de onda debe satisfacer a unas condiciones adicionales y ante todo, la función x, y, z debe ser cuadrado integrable. Más adelante en lugar de hablar de las funciones y valores propios de la ecuación diferencial en la mecánica cuántica hablaremos sobre las funciones y valores propios del operador asociado con la observable. Se supone que la observable L en cualquier resultado de medición solo puede adquirir uno de los valores L1, L2, L3 , , Ln correspondientes a valores del operador asociado con la observable L.. En cada de estos estados la incertidumbre es cero ( L2 0 ) y la observable es igual a uno de los valores permitidos del conjunto L1, L2, L3 , , Ln llamado el espectro de la observable L. El espectro puede ser discreto si los valores propios son contables, separados e individuales L1, L2, L3 , o un conjunto de bandas separadas si valores propios se ubican dentro las franjas L1 L L2, L3 L L4 , o continúo cuando cualquier valor de L es permitido. En el caso del espectro discreto hablan de “cuantización” Mecánica Cuántica a diferencia de la teoría de Bohr propone un método general para encontrar los valores permitidas de observables, reduciendo este problema a la búsqueda de valores y funciones propias de un operador autoadjunto asociado a esta observable. Como los valores propios de los operadores autoadjuntos son reales esto garantiza que valores esperados de las observables también son reales.