Trabajo Práctico Obligatorio 1 - Ingeniería en Automatización y

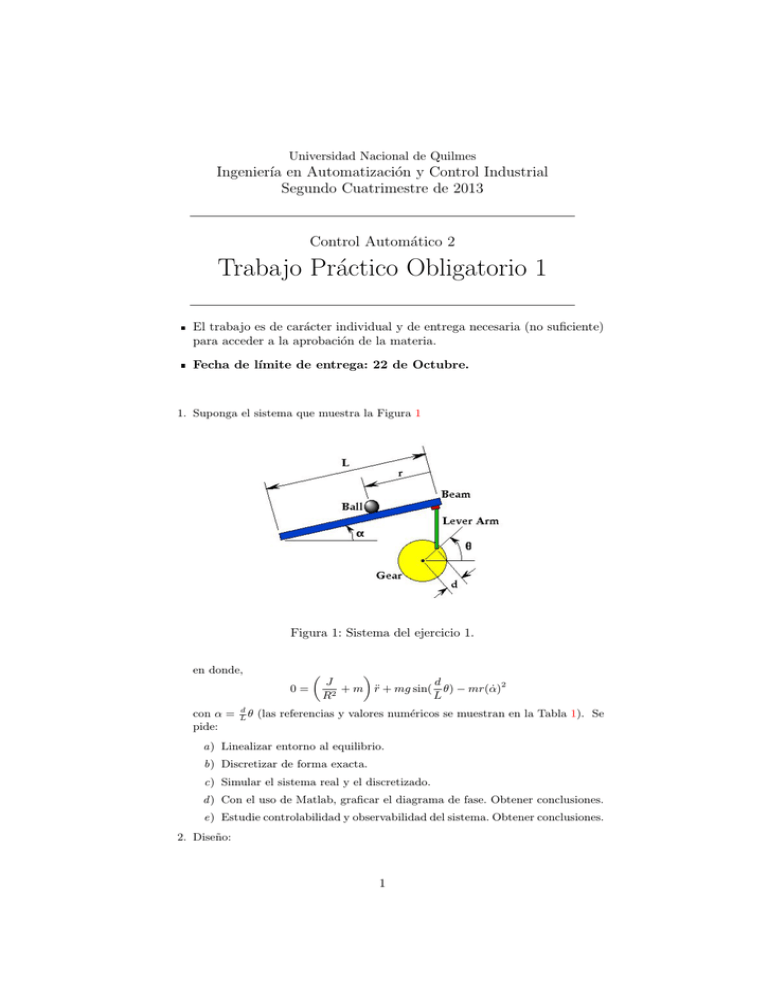
Universidad Nacional de Quilmes
Ingenierı́a en Automatización y Control Industrial
Segundo Cuatrimestre de 2013
Control Automático 2
Trabajo Práctico Obligatorio 1
El trabajo es de carácter individual y de entrega necesaria (no suficiente)
para acceder a la aprobación de la materia.
Fecha de lı́mite de entrega: 22 de Octubre.
1. Suponga el sistema que muestra la Figura 1
Figura 1: Sistema del ejercicio 1.
en donde,
0=
con α =
pide:
d
θ
L
J
d
+
m
r̈ + mg sin( θ) − mr(α̇)2
R2
L
(las referencias y valores numéricos se muestran en la Tabla 1). Se
a) Linealizar entorno al equilibrio.
b) Discretizar de forma exacta.
c) Simular el sistema real y el discretizado.
d ) Con el uso de Matlab, graficar el diagrama de fase. Obtener conclusiones.
e) Estudie controlabilidad y observabilidad del sistema. Obtener conclusiones.
2. Diseño:
1
M
R
d
g
L
J
r
α
θ
Masa de la bola
Radio de la bola
Desplazamiento desde el eje del brazo
Aceleración de la gravedad
Largo del brazo
Momento de Inercia de la bola
Posición de la bola
Angulo del brazo
Angulo de la rueda
0,11 Kg
0,015 m
0,03 m
9,8 m/s2
1m
−6
9,99 × 10 kgm2
Cuadro 1: Valores númericos y referencias del ejercicio 1
a) Diseñe, mediante asignación de polos (técnicas vistas en Control Automático 1), un controlador tal que este defina una ganancia de continua unitaria
para el sistema a lazo cerrado (T0 (s)).
b) Discretize el controlador obtenido mediante una discretazación exacta.
c) Implemente este controlador en simulación (controle el sistema real). Evalúe
la ”robustez ”del controlador perturbando al sistema.
d ) Tenga en cuenta que ocurre en los instantes que van entre dos muestras
consecutivas. Saque conclusiones.
e) Piense como implementarı́a este controlador en un microcontrolador.
Opcional:
f ) En un script de Matlab (o cualquier otro software de cálculo) implemente
una rutina que simule la implementación digital en un microcontrolador
(estructura for ).
3. Analizar la estabilidad a través de la ecuación de Lyapunov, del sistema cuya
matriz de estados viene dada por:
0
1
A =
−0,5 1
Nota: realiza los cálculos manualmente, luego verifique en Matlab.
4. Los tests de autovectores de Popov-Belevitch-Hautus (PBH) dan condiciones
necesarias y suficientes para la controlabilidad y observabilidad de un sistema
lineal estacionario definido por (A, B, C).
Test PBH de Controlabilidad. Un sistema lineal estacionario es controlable
si y solo si, para todo autovector izquierdo v de A (v T A = λv T ) se cumple
que v T B 6= 0.
Test PBH de Observabilidad. Un sistema lineal estacionario es observable
si y solo si para todo autovector derecho u de A (Au = λu) se cumple que
Cu 6= 0.
Usando los resultados de Popov-Belevitch-Hautus, se pide:
a) Mostrar que la controlabilidad es una propiedad invariante con respecto a
la realimentación de estados: si el par (A,B) es controlable, entonces el par
(A + BK, B) es controlable para cualquier K.
b) Mostrar que la observabilidad no es una propiedad invariante con respecto
a la realimentación de estados: si el par (A,C) es observable, el par (A +
BK,C) puede no ser observable para algún K.
2