1 Indique las opciones que contienen un conjunto ortogonal de
Anuncio
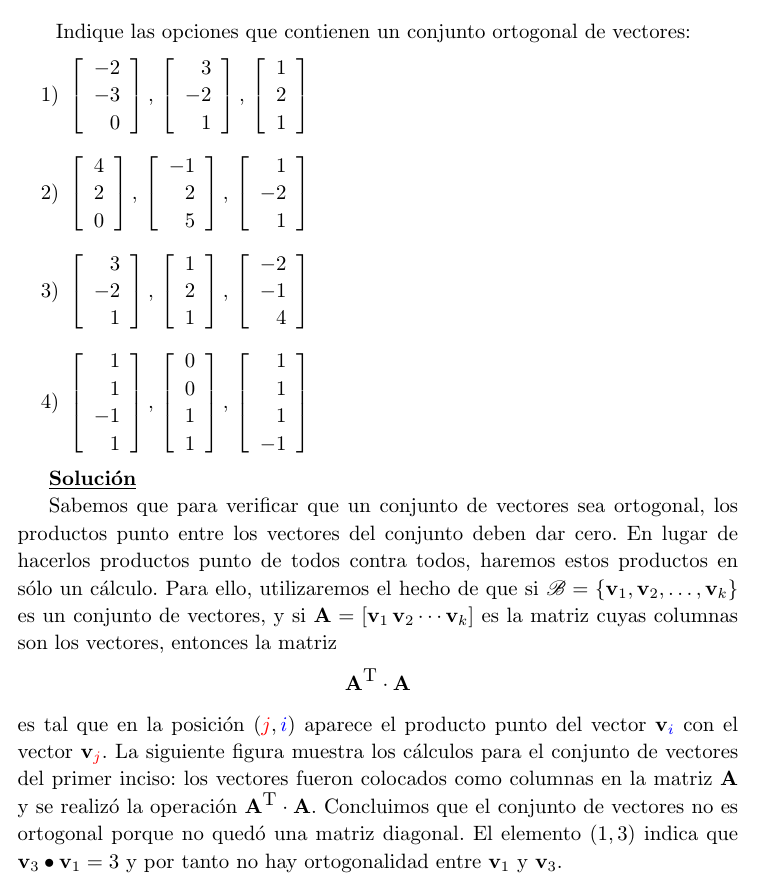
Indique las opciones que contienen un conjunto ortogonal de vectores:
−2
3
1
1) −3 , −2 , 2
0
1
1
4
−1
1
2) 2 , 2 , −2
0
5
3
3) −2 ,
1
1
1
4)
−1 ,
1
1
1
2 ,
1
0
0
1 ,
−2
−1
4
1
1
1
1
−1
Solución
Sabemos que para verificar que un conjunto de vectores sea ortogonal, los
productos punto entre los vectores del conjunto deben dar cero. En lugar de
hacerlos productos punto de todos contra todos, haremos estos productos en
sólo un cálculo. Para ello, utilizaremos el hecho de que si B = {v1 , v2 , . . . , vk }
es un conjunto de vectores, y si A = [v1 v2 · · · vk ] es la matriz cuyas columnas
son los vectores, entonces la matriz
AT · A
es tal que en la posición (j, i) aparece el producto punto del vector vi con el
vector vj . La siguiente figura muestra los cálculos para el conjunto de vectores
del primer inciso: los vectores fueron colocados como columnas en la matriz A
y se realizó la operación AT · A. Concluimos que el conjunto de vectores no es
ortogonal porque no quedó una matriz diagonal. El elemento (1, 3) indica que
v3 • v1 = 3 y por tanto no hay ortogonalidad entre v1 y v3 .
Los cálculos que siguen a AT · A son las comprobaciones a que los productos
vi • vj efectivamente son los elementos (j, i) de la matriz. Esta comprobación
requiere que se tenga programada la función col que entrega una cierta columna
de una matriz.











