Capítulo

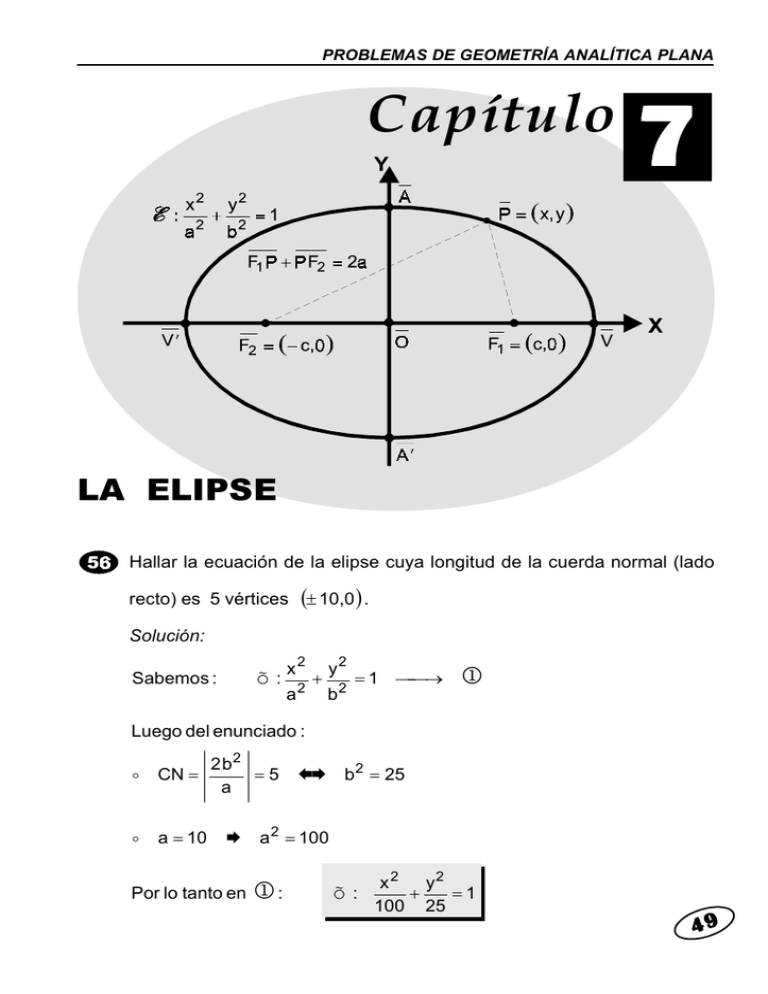
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Capítulo
7
LA ELIPSE
Hallar la ecuación de la elipse cuya longitud de la cuerda normal (lado
recto) es 5 vértices (± 10,0 ) .
Solución:
õ:
Sabemos :
x2
y2
+
= 1 →
a 2 b2
!
Luego del enunciado :
!
CN =
!
a = 10
2 b2
= 5 "! b 2 = 25
a
!
Por lo tanto en
a 2 = 100
!:
õ:
x2
y2
+
=1
100 25
49
Capítulo 7. LA ELIPSE
Hallar la ecuación de la elipse, cuyo eje es coincidente con x = 1 , C = (1,5 ) ,
F = (1,8 ) ; suma de las distancias focales de un punto de la elipse es 12.
Solución:
õ:
Del enunciado deducimos :
Pero : 2a = 12
"!
a=6
"!
"!
c2 = 9
Luego : c = CF = 3
Sabemos : b 2 = a 2 − c 2
Por lo tanto :
50
õ:
"!
(x − h)2 + (y − k )2
b2
=1
a 2 = 36
b 2 = 36 − 9 = 27
(x − 1)2 + (y − 5)2
27
a2
36
=1
"! b 2 = 27
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Reducir la ecuación x 2 + 4 y 2 − 6 x + 16 y + 21 = 0 a la forma ordinaria de
la ecuación de una elipse y determinar las coordenadas del centro, vértices
y focos, las longitudes de los ejes mayor y menor, y la cuerda normal; y la
excentricidad.
Solución:
x 2 + 4 y 2 − 6x + 16y + 21 = 0
Completando cuadrados para x e y :
(x
2
) (
)
− 6x + 9 + 4 y 2 + 4y + 4 = −21 + 9 + 16
(x − 3)2 + 4(y + 2)2 = 4
õ:
(x − 3)2 + (y + 2)2
4
1
=1
De la ecuación tenemos : C = (h,k ) = (3,−2)
Luego los vértices de la elipse se obtienen de :
!
V = (h ± a,k ) = (3 ± 2,−2) !




V1 = (5,−2)
V2 = (1,−2 )
También :
!
a2 = 4
!
a 2 = b2 + c 2
!
a = ±2
!
!
4 = 1+ c2
! Eje mayor : 2a = 2 × 2 = 4
!
b 2 = 1 ! b = ±1
Cuerda Normal : CN =
! Excentricidad : e =
!
!
c2 = 3
!
c2 = ± 3
Eje menor : 2b = 2 × 1 = 2
2b2
2 ×1
=
=1
a
2
c
3
=
<1
a
1
51
Capítulo 7. LA ELIPSE
Por el foco de la elipse x 2 25 + y 2 15 = 1 se ha trazado una perpendicular
a su eje mayor. Determinar las distancias de los puntos de intersección de
esta perpendicular con la elipse hasta los focos.
Solución:
Tenemos la ecuación de la elipse :
!
õ:
x2 y2
+
= 1 →
25 15
Sabemos : b 2 = a 2 − c 2
!
c 2 = a2 − b2
!
!
c = ± 25 − 15 = ± 10
Luego, los focos de la elipse son :
(
! F = (± c,0 ) ! F = ± 10 ,0
)
La ecuación de la perpendicu lar
trazada en el primer foco es :
52
x = 10
→
"
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
De
9 y2
+
=1 !
25 15
! y ":
De aquí : C = (x, y ) =
y2 = 9 !
y = ±3
( 10,3)
Por lo tanto :
!
F1C =
( 10 −
!
F2C =
(−
10
)2 + (0 − 3)2 = 3
10 − 10
)2 + (0 − 3)2 = 7
Búsquese la ecuación de la elipse que tenga como centro C = (− 2,4 ) y
sea tangente a los dos ejes de coordenadas.
Solución:
Sea :
õ:
(x − h)2 + (y − k )2
b2
=1
a2
Para este caso :
! a : Distancia de C al eje X
!
a=4 !
a 2 = 16
! b : Distancia de C al eje Y
! b = 2 ! b2 = 4
!
õ:
(x + 2)2 + (y − 4)2
4
16
=1
53
Capítulo 7. LA ELIPSE
Hallar la ecuación canónica de la elipse, si uno de los vértices está en
V1 = (5,0 ) y pasa por el punto P = (2,3 ) .
Solución:
x2
y2
+
=1
a 2 b2
! õ:
V1 = (5,0 ) !
Dado que :
õ:
Luego :
a=5
!
a 2 = 25
x 2 y2
+
=1
25 b 2
Como : P = (2,3 ) ∈
õ !
75
4
3
+ 2 = 1 ! b2 =
7
25 b
Por lo tanto :
õ:
x2
y2
+
=1 !
25 75 7
õ : 3x 2 + 7y 2 = 75
La base de un auditorio es de forma elíptica, tiene 20 m. de longitud y 16 m
de ancho. Si cae una aguja sobre un foco el ruido que produce se escucha
claramente cerca del otro foco. ¿A qué distancia está un foco del otro
foco?
Solución:
Según
losdatos
datosdel
del
enunciado:
Segúnlos
enunciado
:
! a = 10 ! a2 = 100
! b = 8 ! b2 = 64
De donde : b2 = a2 − c 2
Porlo
lotanto
tanto:
Por
:
54
! c 2 = 36 ! c = ±6
F1F2 = 2c = 12
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Usando la definición de elipse, obtener la ecuación de la elipse con focos
en F = (− 3,4 ) y F2 = (5,4 ) eje mayor 12.
Solución:
Sea P = (x, y ) el punto que se mueve.
Por la definición de elipse, se tiene que :
!
F1P − F2P = 2a = 12
De donde :
!
(x + 3)2 + (y − 4)2 − (x − 5)2 + (y − 4)2
= 12
Efectuando operaciones :
õ : 5x 2 − 9y 2 + 10x + 72y + 31 = 0
55
Capítulo 7. LA ELIPSE
Demostrar que para todo elipse que tenga su centro en el origen, la distancia
de cualquiera de los extremos del eje menor a cualquiera de los focos es la
mitad de la longitud del eje mayor.
Solución:
Sea
õ:
x2
a2
+
y2
b2
= 1 la elipse con vértice en el origen.
Probar que :
!
B1 F1 =
V1 V2
2
Luego, de la figura :
=
2a
=a
2
B1 F1 =
c 2 + b2
pero, sabemos por definición que : a 2 = c 2 + b 2
Por lo tanto :
56
B1 F1 = a 2 = a
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Un punto se mueve de tal modo que la suma de las distancias de los
puntos A = (− 2,0 ) y B = (− 2,6 ) es 8. Hallar la ecuación del lugar
geométrico de P .
Solución:
Sea P = (x, y ) el punto que se mueve.
:
Por la
la condición
condicióndel
delproblema
problema:
AP + BP = 8
De donde :
(x + 2)2 + y 2
+
(x + 2)2 + (y − 6 )2
=8
Efectuando operacione s, se tiene :
õ : 16 x 2 + 7 y 2 + 64 x − 42y + 15 = 0
(x + 2)2 + (y − 3 )2
∴ õ:
7
16
=1
La órbita que describe la Tierra alrededor del Sol es aproximadamente una
elipse, con el Sol en uno de los focos. Si el eje mayor de la órbita elíptica
es de 300 000 km. y la excentricidad es de 0,017 aproximadamente.
Hallar la distancia máxima y mínima de la Tierra al Sol.
Solución:
De los datos y según el gráfico, tenemos que :
!
2a = 300 000
!
a = 150 000
Del valor aproximado de la excentricidad de la elipse :
!
e=
c
= 0,017 !
a
c = 0,017 × a = 0,017 × 150 000
!
c = 2 550
57
Capítulo 7. LA ELIPSE
Luego :
! Máximo : a + c = 150 000 + 2 550 !
a + c = 152 550
a − c = 150 000 − 2 550 !
a − c = 147 450
´
! Minimo
:
58