2. Ley de Hooke

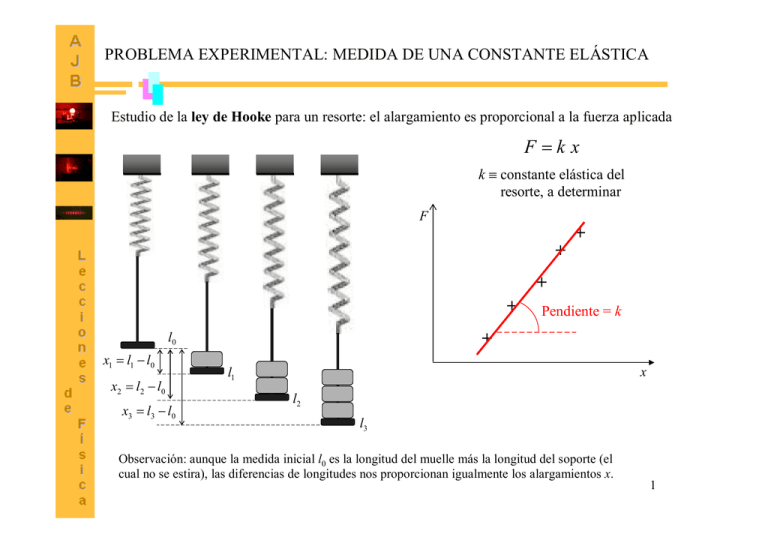
PROBLEMA EXPERIMENTAL: MEDIDA DE UNA CONSTANTE ELÁSTICA
Estudio de la ley de Hooke para un resorte: el alargamiento es proporcional a la fuerza aplicada
F k x
k  constante elástica del
. resorte, a determinar
F
+
+
+
+
+
l0
x1  l1  l0
x2  l 2  l 0
x3  l3  l0
Pendiente = k
x
l1
l2
l3
Observación: aunque la medida inicial l0 es la longitud del muelle más la longitud del soporte (el
cual no se estira), las diferencias de longitudes nos proporcionan igualmente los alargamientos x.
1
EJEMPLO DE MEDIDAS Y TRATAMIENTO DE DATOS
m (g)
0
20
30
50
60
70
Dm (g)
0
0,2
0,3
0,5
0,6
0,7
l (mm)
375
435
467
527
559
587
Dl (mm)
2
2
2
2
2
2
x = l - l 0 (m)
Dx (m)
F = mg (N)
DF (N)
0,435
0,467
0,527
0,559
0,587
0,004
0,004
0,004
0,004
0,004
0,196
0,294
0,490
0,588
0,686
0,002
0,003
0,005
0,006
0,007
Errores en las medidas
Valores crecientes l
Error Dm: se usan pesas de (10.0  0.1) g, por tanto el
error por cada pesa añadida es  0.1 g.
A medir
constante k
Tratamiento de datos
Masas m
Medida de
longitudes l
Error Dl: la regla aprecia mm, pero tendremos en cuenta
que cuando se añaden las pesas el muelle oscila un poco.
Por eso tomamos como error de cada longitud  2 mm.
Alargamiento
x  l  l0
Dx  Dl  Dl0
Fuerza
F mg
DF  Dm  g
(Suponemos que el valor de la gravedad se conoce con una
precisión mucho mayor que los demás factores que intervienen,
por lo que su error es despreciable frente a los otros).
2
AJUSTE MANUAL DE DATOS PARA OBTENER LA CONSTANTE ELÁSTICA
x = l - l 0 (m)
Dx (m)
F = mg (N)
DF (N)
0,435
0,467
0,527
0,559
0,587
0,004
0,004
0,004
0,004
0,004
0,196
0,294
0,490
0,588
0,686
0,002
0,003
0,005
0,006
0,007
F (N)
mexp
0.600
mexp
Dmexp 
N
DN 
mexp
D
N  N A  N B  0.700  0.180  0.520 N
DN A  0.007
DN  0.009 N
D  DA  DB  0.590  0.432  0.158 m
DDA  0.004
DDB  0.004
mexp 
1
N
DN   2 DD
D
D
Dmexp 
DD  0.008 N
Exceso decimales
N A  0.700
N

D
DD 
DN B  0.002
N 0.520

 3.291 N/m
D 0.158
0.009 0.520  0.008

 0.224  0.2 N/m
0.158
0.158 2
k  mexp  3.3  0.2  N/m
N
0.400
Comparación:
aplicando el método de mínimos
cuadrados el resultado obtenido es
k  mexp  3.22  0.11 N/m
D
0.200
N B  0.180
DB  0.432
DA  0.590
3
0.400
0
1
2
3
4
0.5
500
6
7
8
9
010
.600
11x (m)12
ADDENDA: AJUSTE MANUAL DE DATOS DE REGRESIÓN
x
x1
x2
…
…
xn
Dx
Dx 1
Dx 2
Dx n
y
y1
y2
…
…
yn
Dy
Dy 1
Dy 2
1º) Plotear los puntos experimentales sobre papel milimetrado
(No es preciso plotear las barras de error, pero hay que tenerlas en cuenta en cálculos posteriores)
2º) Trazar una recta de ajuste que deje a ambos lados igual número de puntos
3º) Construir un triángulo rectángulo de catetos próximos a los extremos A, B
Dy n
4º) Calcular la pendiente experimental
mexp 
Y
N
D
N  N A  NB
Dmexp
NA
mexp
1
N

DN 
DD  DN   2 DD
D
D
N
D
DD  DDA  DDB
(Como errores NA, NB se aceptan
los de los puntos experimentales
más próximos)
N
mexp
B
NB
D
DB
0
1
2
3
4
5
6
7
8
D  DA  DB
DN  DN A  DN B
A
Error en la pendiente:
mexp
donde
DA
9
10
11
X
12
5º) Ordenada en el origen
Se prolonga la recta de ajuste
hasta cortar el eje Y, y se
adopta como error el más
grande de los dos siguientes:
•El del punto más próximo
•El promedio de los errores
4