parcial 1

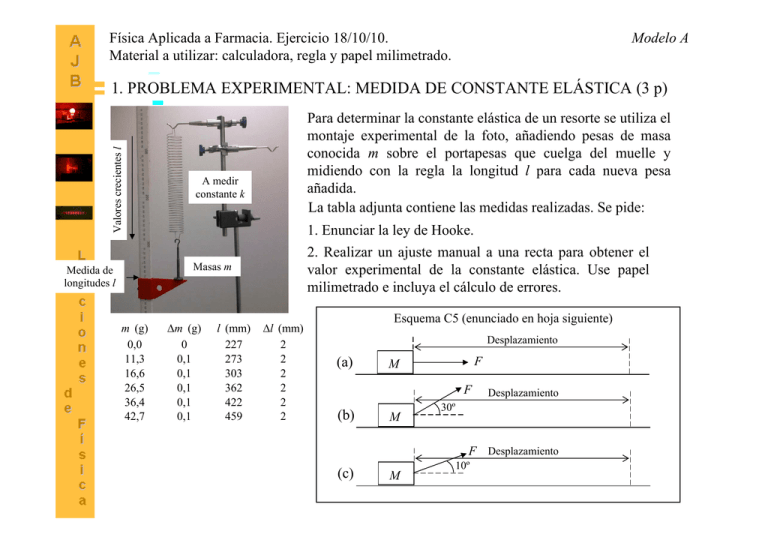
Física Aplicada a Farmacia. Ejercicio 18/10/10.
Material a utilizar: calculadora, regla y papel milimetrado.
Modelo A
Valores crecientes l
1. PROBLEMA EXPERIMENTAL: MEDIDA DE CONSTANTE ELÁSTICA (3 p)
Para determinar la constante elástica de un resorte se utiliza el
montaje experimental de la foto, añadiendo pesas de masa
conocida m sobre el portapesas que cuelga del muelle y
midiendo con la regla la longitud l para cada nueva pesa
añadida.
La tabla adjunta contiene las medidas realizadas. Se pide:
A medir
constante k
1. Enunciar la ley de Hooke.
2. Realizar un ajuste manual a una recta para obtener el
valor experimental de la constante elástica. Use papel
milimetrado e incluya el cálculo de errores.
Masas m
Medida de
longitudes l
m (g)
0,0
11,3
16,6
26,5
36,4
42,7
∆m (g)
0
0,1
0,1
0,1
0,1
0,1
l (mm)
227
273
303
362
422
459
∆l (mm)
2
2
2
2
2
2
Esquema C5 (enunciado en hoja siguiente)
Desplazamiento
(a)
F
M
F
(b)
M
Desplazamiento
30º
F Desplazamiento
(c)
M
10º
1
Modelo A
2. PROBLEMA BIOMECÁNICA (3 p).
El músculo deltoides levanta el brazo hasta la posición
horizontal. En una persona adulta típica podemos suponer
que este músculo se inserta a una distancia x1 = 15 cm de
la articulación del hombro y en posición horizontal la
fuerza que ejerce forma un ángulo θ = 18º con el húmero.
Para un peso del brazo W = 35 N aplicado a una distancia
x2 = 35 cm de la articulación del hombro, se pide:
1. ¿De qué género de palanca se trata?
2. La tensión T ejercida por el músculo.
3. Las componentes de la reacción sobre la articulación,
RX y RY, así como su módulo R y el ángulo que forma el
vector R con el eje horizontal..
Y
T
X
θ
RX
RY
x1
x2
W
CUESTIONES. Cuestión 3: 1.5 p. Cuestión 4: 1.5 p. Cuestión 5: 1 p.
3. Se quiere preparar una disolución 0.1 M de una sal cuyo peso fórmula es M = 58.5 g/mol
(considérese exacto). Para ello se pesan 0.294 g de la sal con una balanza que aprecia 0.001 g,
y se disuelven en 50 ml de agua destilada medidos con una pipeta que aprecia 0.2 ml. ¿Qué
valor debemos admitir para la molaridad de la disolución y cuál es el error absoluto?
4. Definir brevemente las fuerzas de rozamiento estática y dinámica y explicar qué diferencias
existen entre ellas. ¿Cuál es el umbral para que se inicie el movimiento?.
5. En el esquema C5 de la hoja anterior se han dibujado tres casos distintos en que la
aplicación de una misma fuerza provoca el mismo desplazamiento de un cuerpo de masa M
sobre una superficie horizontal. Ordenar razonadamente de mayor a menor el trabajo realizado
2
por la fuerza F en los tres casos.
Física Aplicada a Farmacia. Ejercicio 18/10/10.
Material a utilizar: calculadora, regla y papel milimetrado.
Modelo B
Valores crecientes l
1. PROBLEMA EXPERIMENTAL: MEDIDA DE CONSTANTE ELÁSTICA (3 p)
A medir
constante k
1. Enunciar la ley de Hooke.
2. Realizar un ajuste manual a una recta para obtener el
valor experimental de la constante elástica. Use papel
milimetrado e incluya el cálculo de errores.
Masas m
Medida de
longitudes l
m (g)
0,0
22,6
33,1
53,0
72,8
85,3
Para determinar la constante elástica de un resorte se utiliza el
montaje experimental de la foto, añadiendo pesas de masa
conocida m sobre el portapesas que cuelga del muelle y
midiendo con la regla la longitud l para cada nueva pesa
añadida.
La tabla adjunta contiene las medidas realizadas. Se pide:
∆m (g)
0
0,1
0,1
0,1
0,1
0,1
l (mm)
227
500
530
589
649
686
∆l (mm)
2
2
2
2
2
2
Esquema C5 (enunciado en hoja siguiente)
Desplazamiento
(a)
F
M
F
(b)
M
Desplazamiento
30º
F Desplazamiento
(c)
M
10º
3
Modelo B
2. PROBLEMA BIOMECÁNICA (3 p).
El músculo deltoides levanta el brazo hasta la posición
horizontal. En un culturista bien entrenado podemos suponer
que este músculo se inserta a una distancia x1 = 19 cm de la
articulación del hombro y en posición horizontal la fuerza
que ejerce forma un ángulo θ = 12º con el húmero. Para un
peso del brazo W = 45 N aplicado a una distancia x2 = 40 cm
de la articulación del hombro, se pide:
Y
T
1. ¿De qué género de palanca se trata?
2. La tensión T ejercida por el músculo.
3. Las componentes de la reacción sobre la articulación,
RX y RY, así como su módulo R y el ángulo que forma el
vector R con el eje horizontal..
X
θ
RX
RY
x1
x2
W
CUESTIONES. Cuestión 3: 1.5 p. Cuestión 4: 1.5 p. Cuestión 5: 1 p.
3. Se quiere preparar una disolución 0.1 M de una sal cuyo peso fórmula es M = 58.5 g/mol
(considérese exacto). Para ello se pesan 0.592 g de la sal con una balanza que aprecia 0.001 g,
y se disuelven en 100 ml de agua destilada medidos con una probeta graduada que aprecia 0.5
ml. ¿Qué valor debemos admitir para la molaridad de la disolución y cuál es el error absoluto?
4. Definir brevemente las fuerzas de rozamiento estática y dinámica y explicar qué diferencias
existen entre ellas. ¿Cuál es el umbral para que se inicie el movimiento?.
5. En el esquema C5 de la hoja anterior se han dibujado tres casos distintos en que la
aplicación de una misma fuerza provoca el mismo desplazamiento de un cuerpo de masa M
sobre una superficie horizontal. Ordenar razonadamente de mayor a menor el trabajo realizado
4
por la fuerza F en los tres casos.
1. PROBLEMA EXPERIMENTAL (3 p). Modelo A
m (g)
0,0
11,3
16,6
26,5
36,4
42,7
F (N)
∆m (g)
0
0,1
0,1
0,1
0,1
0,1
l (mm)
227
273
303
362
422
459
PROCESADO DE DATOS
∆l (mm) x = l - l 0 (m)
∆x (m)
F = mg (N)
2
2
0,046
0,004
0,111
2
0,076
0,004
0,163
2
0,135
0,004
0,260
2
0,195
0,004
0,357
2
0,232
0,004
0,418
0,5
0,4
0,3
N=
∆N =
D =
∆D =
m exp =
0,340
0,002
0,205
0,008
1,66
∆m exp =
0,07
N A = (0.440 ± 0.001) N
N = N A − N B = 0.440 − 0.100 = 0.340 N
∆N = ∆N A + ∆N B = 0.001 + 0.001 = 0.002 N
N B = (0.100 ± 0.001) N
N
D = DA − DB = 0.245 − 0.040 = 0.205 m
∆D = ∆DA + ∆DB = 0.004 + 0.004 = 0.008 N
0,2
k = mexp = (1.66 ± 0.07 ) N/m
mexp
D
0,1
N A = (0.245 ± 0.004 ) m
DB = (0.040 ± 0.004 ) m
0,0
0,00
mexp =
0,05
N
D
∆mexp =
0,10
∂mexp
∂N
0,15
∆N +
∂mexp
∂D
0,20
∆D =
0,25
N
1
∆N + − 2 ∆D
D
D
x (m)
∆F (N)
0,001
0,001
0,001
0,001
0,001
1. PROBLEMA EXPERIMENTAL (3 p). Modelo B
F (N)
1,0
m (g)
∆m (g)
0,0
N A = (0.900 ± 0.001) N0
22,6
0,1
33,1
0,1
53,0
0,1
72,8
0,1
85,3
0,1
0,9
0,8
0,7
0,6
0,5
N=
∆N =
D =
∆D =
m exp =
0,700
0,002
0,215
0,008
3,26
∆m exp =
0,13
l (mm)
227
500
530
589
649
686
∆l (mm)
2
2
2
2
2
2
DA = (0.265 ± 0.004 ) m
F (N)
0,8
0,7
0,6
0,5
0,10
0,15
N=
∆N =
D =
∆D =
m exp =
0,670
0,002
0,205
0,008
3,27
∆m exp =
0,14
0,20
0,25
0,30
∆D = ∆DA + ∆DB = 0.004 + 0.004 = 0.008 N
DA = (0.480 ± 0.004 ) m
0,35
0,40
0,45
0,50
k = mexp = (3.26 ± 0.13) N/m
x (m)
N A = (0.870 ± 0.001) N
mexp =
N
D
∆mexp =
∂mexp
∂N
∆N +
∂mexp
∂D
∆D =
1
N
∆N + − 2 ∆D
D
D
N = N A − N B = 0.870 − 0.200 = 0.670 N
N B = (0.200 ± 0.001) N
N
∆N = ∆N A + ∆N B = 0.001 + 0.001 = 0.002 N
D = DA − DB = 0.470 − 0.265 = 0.205 m
0,4
∆D = ∆DA + ∆DB = 0.004 + 0.004 = 0.008 N
0,3
k = mexp = (3.27 ± 0.14 ) N/m
D
0,2
DA
0,1
0,20
= (0.265 ± 0.004 ) m
0,25
0,30
0,001
0,001
0,001
0,001
0,001
D = DA − DB = 0.480 − 0.265 = 0.215 m
D
N B = (0.200 ± 0.001) N
0,05
0,221
0,324
0,519
0,713
0,836
∆N = ∆N A + ∆N B = 0.001 + 0.001 = 0.002 N
mexp
0,0
0,00
0,9
0,004
0,004
0,004
0,004
0,004
N = N A − N B = 0.900 − 0.200 = 0.700 N
0,3
0,1
0,273
0,303
0,362
0,422
0,459
∆F (N)
N
0,4
0,2
PROCESADO DE DATOS
∆x (m)
F = mg (N)
x = l - l 0 (m)
0,35
0,40
DA = (0.470 ± 0.004 ) m
0,45
0,50 x (m)
2. PROBLEMA BIOMECÁNICA (3 p). Modelo A
El músculo deltoides levanta el brazo hasta la posición horizontal. En una persona adulta típica
podemos suponer que este músculo se inserta a una distancia x1 = 15 cm de la articulación del
hombro y en posición horizontal la fuerza que ejerce forma un ángulo θ = 18º con el húmero.
Para un peso del brazo W = 35 N aplicado a una distancia x2 = 35 cm de la articulación del
hombro, se pide:
1. ¿De qué género de palanca se trata?
2. La tensión T ejercida por el músculo.
3. Las componentes de la reacción sobre la articulación,
RX y RY, así como su módulo R y el ángulo que forma el
F
vector R con el eje horizontal..
R
1. El fulcro es la articulación del hombro, es una palanca de
3er
género.
2. Tomamos como origen de coordenadas O la articulación del hombro
y calculamos T a partir de la ecuación de momentos.
x ⋅W
T= 2
τ O = T ⋅ x1 ⋅ sin (180 − θ ) − W ⋅ x2 ⋅ sin 90º = 0
x1 ⋅ sin θ
∑
T
Y
180 − θ
O
RY
T sin θ
W
f
Cálculo numérico:
35 cm ⋅ 35 N
T=
= 264 N
15 cm ⋅ sin 18
θ
X
f
RX
W
x1
x2
Véase que la fuerza que ha de ejercer el
músculo es bastante más grande que el
peso W.
2. PROBLEMA BIOMECÁNICA Continuación (3 p). Modelo A
3. Cálculo de las componentes de la reacción sobre la articulación, módulo y ángulo.
T
Y
RX
180 − θ
β
θ
X
O
RY
RX
W
x1
x2
∑
FX = −T ⋅ cos θ + RX = 0
Y
Y
R
R = RX2 + RY2 = 2512 + 47 2 = 256 N
RX = T ⋅ cos θ
RX = 264 ⋅ cos18º = 251 N
∑ F = T ⋅ sin θ − R − W = 0
RY
RY = T ⋅ sin θ − W
RY = 264 ⋅ sin 18 − 35 = 47 N
tan β =
RY
47
=
= 0.1857
251
RX
β = 10.5º
2. PROBLEMA BIOMECÁNICA (3 p). Modelo B
El músculo deltoides levanta el brazo hasta la posición horizontal. En un culturista bien
entrenado podemos suponer que este músculo se inserta a una distancia x1 = 19 cm de la
articulación del hombro y en posición horizontal la fuerza que ejerce forma un ángulo θ = 12º
con el húmero. Para un peso del brazo W = 45 N aplicado a una distancia x2 = 40 cm de la
articulación del hombro, se pide:
1. ¿De qué género de palanca se trata?
2. La tensión T ejercida por el músculo.
3. Las componentes de la reacción sobre la articulación,
RX y RY, así como su módulo R y el ángulo que forma el
F
vector R con el eje horizontal..
R
1. El fulcro es la articulación del hombro, es una palanca de
3er
género.
2. Tomamos como origen de coordenadas O la articulación del hombro
y calculamos T a partir de la ecuación de momentos.
x ⋅W
T= 2
τ O = T ⋅ x1 ⋅ sin (180 − θ ) − W ⋅ x2 ⋅ sin 90º = 0
x1 ⋅ sin θ
∑
T
Y
180 − θ
O
RY
T sin θ
W
f
Cálculo numérico:
40 cm ⋅ 45 N
T=
= 456 N
19 cm ⋅ sin 12
θ
X
f
RX
W
x1
x2
Véase que la fuerza que ha de ejercer el
músculo es bastante más grande que el
peso W.
2. PROBLEMA BIOMECÁNICA Continuación (3 p). Modelo B
3. Cálculo de las componentes de la reacción sobre la articulación, módulo y ángulo.
T
Y
RX
180 − θ
β
θ
X
O
RY
RX
W
x1
x2
∑
FX = −T ⋅ cos θ + RX = 0
Y
Y
R
R = RX2 + RY2 = 446 2 + 50 2 = 448 N
RX = T ⋅ cos θ
R X = 456 ⋅ cos 12º = 446 N
∑ F = T ⋅ sin θ − R − W = 0
RY
RY = T ⋅ sin θ − W
RY = 456 ⋅ sin 12 − 45 = 50 N
tan β =
RY
50
=
= 0.1116
446
RX
β = 6.5º
Modelo A
3. Se quiere preparar una disolución 0.1 M de una sal cuyo peso fórmula es M = 58.5 g/mol
(considérese exacto). Para ello se pesan 0.294 g de la sal con una balanza que aprecia 0.001 g,
y se disuelven en 50 ml de agua destilada medidos con una pipeta que aprecia 0.2 ml. ¿Qué
valor debemos admitir para la molaridad de la disolución y cuál es el error absoluto?
M=
m a / PF
1 ⎛a⎞
=
=
⎜ ⎟
V
V
PF ⎝ V ⎠
∆M =
a
1 ⎛1
⎞
⎜ ∆a + 2 ∆V ⎟
PF ⎝ V
V
⎠
M=
m a / PF
=
V
V
M = molaridad
m = moles a = nº gramos PF = peso fórmula
PF (g/mol) =
a (g) =
∆a (g) =
V (ml) =
∆V (ml) =
58,5
0,294
0,001
50
0,2
V (l) =
∆V (l) =
M (mol/l) =
∆M (mol/l) =
V = volumen disol.
0,0500
0,0002
0,1005
0,0007
M = (0.1005 ± 0.0007 ) mol/l
Modelo B
3. Se quiere preparar una disolución 0.1 M de una sal cuyo peso fórmula es M = 58.5 g/mol
(considérese exacto). Para ello se pesan 0.592 g de la sal con una balanza que aprecia 0.001 g,
y se disuelven en 100 ml de agua destilada medidos con una pipeta que aprecia 0.5 ml. ¿Qué
valor debemos admitir para la molaridad de la disolución y cuál es el error absoluto?
M=
m a / PF
1 ⎛a⎞
=
=
⎜ ⎟
V
V
PF ⎝ V ⎠
∆M =
a
1 ⎛1
⎞
⎜ ∆a + 2 ∆V ⎟
PF ⎝ V
V
⎠
M=
m a / PF
=
V
V
M = molaridad m = moles a = nº gramos PF = peso fórmula
PF (g/mol) =
a (g) =
∆a (g) =
V (ml) =
∆V (ml) =
58,5
0,592
0,001
100
0,5
V (l) =
∆V (l) =
M (mol/l) =
∆M (mol/l) =
M = (0.1012 ± 0.0007 ) mol/l
V = volumen disol.
0,1000
0,0005
0,1012
0,0007
Modelos A y B
4. Definir brevemente las fuerzas de rozamiento estática y dinámica y explicar qué diferencias
existen entre ellas. ¿Cuál es el umbral para que se inicie el movimiento?.
Véase tema 2: Dinámica, transparencias 19 - 23
5. En el esquema C5 de la hoja anterior se han dibujado tres casos distintos en que la
aplicación de una misma fuerza provoca el mismo desplazamiento de un cuerpo de masa M
sobre una superficie horizontal. Ordenar razonadamente de mayor a menor el trabajo realizado
por la fuerza F en los tres casos.
Desplazamiento
(a)
F
M
F
(b)
M
Para un cuerpo que se mueve a lo largo
de una trayectoria rectilínea:
d
Desplazamiento
W = F ⋅ d ⋅ cos θ
30º
d
Siendo iguales F y d, el trabajo será
mayor cuando cos θ sea mayor.
F Desplazamiento
(c)
M
F: fuerza aplicada
d: desplazamiento
θ: ángulo entre F y d
10º
d
El orden de trabajos realizados por F es
Mayor
Menor
Esquema (a): θ = 0 ⇒ cos θ = 1
Esquema (c): θ = 10º ⇒ cos θ = 0.9848
Esquema (b): θ = 30º ⇒ cos θ = 0.8660