Funciones uno a uno e inversas

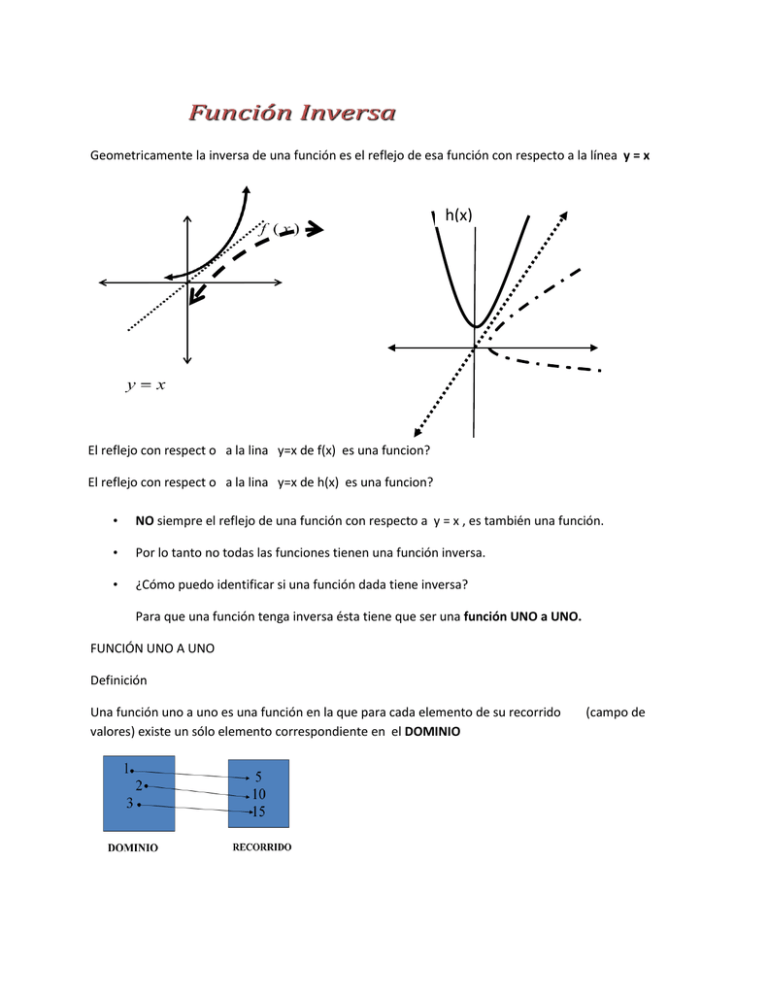
Geometricamente la inversa de una función es el reflejo de esa función con respecto a la línea y = x
h(x)
El reflejo con respect o a la lina y=x de f(x) es una funcion?
El reflejo con respect o a la lina y=x de h(x) es una funcion?
•
NO siempre el reflejo de una función con respecto a y = x , es también una función.
•
Por lo tanto no todas las funciones tienen una función inversa.
•
¿Cómo puedo identificar si una función dada tiene inversa?
Para que una función tenga inversa ésta tiene que ser una función UNO a UNO.
FUNCIÓN UNO A UNO
Definición
Una función uno a uno es una función en la que para cada elemento de su recorrido
valores) existe un sólo elemento correspondiente en el DOMINIO
(campo de
PRUEBA DE LA LÍNEA HORIZONTAL
Para determinar si una gráfica dada corresponde a una función uno a uno utilizamos la
prueba de la línea horizontal. Si la gráfica de una función toca un solo punto a traves
de toda línea horizontal que se dibuje en el dominio de la function, ésta
corresponde a una función uno a uno.
Existe alguna línea horizontal que toque dos puntos de esta gráfica a la misma vez?
Identifica cuáles de las siguientes funciones son uno a uno.
”
Sea f una función uno a uno, denotamos la inversa de f de la siguiente forma:
NOTACIÓN
“ función inversa de f(x)”
f(x)
Procedimiento para hallar la función inversa de f(x)
1. Expresar la función en término de las variables x y y.
2. Intercambiar en la ecuación la x por la y y viceversa.
3. Despejar la ecuación para y , (variable dependiente) .
4. Expresar la ecuación en notación de función inversa .
Halla la función inversa de las siguientes funciones uno a uno.
1.
2. g ( x)
x3 1
3.
h( x )
1
x 2
Prueba para verificar si dos funciones dadas f y g, una es inversa de la otra. Sean f y g dos funciones
uno a uno, si g es función inversa de f entonces:
f ( g ( x))
x y
g ( f ( x))
x