2.3. Funciones par e impar 2.4. Expansiones de medio periodo

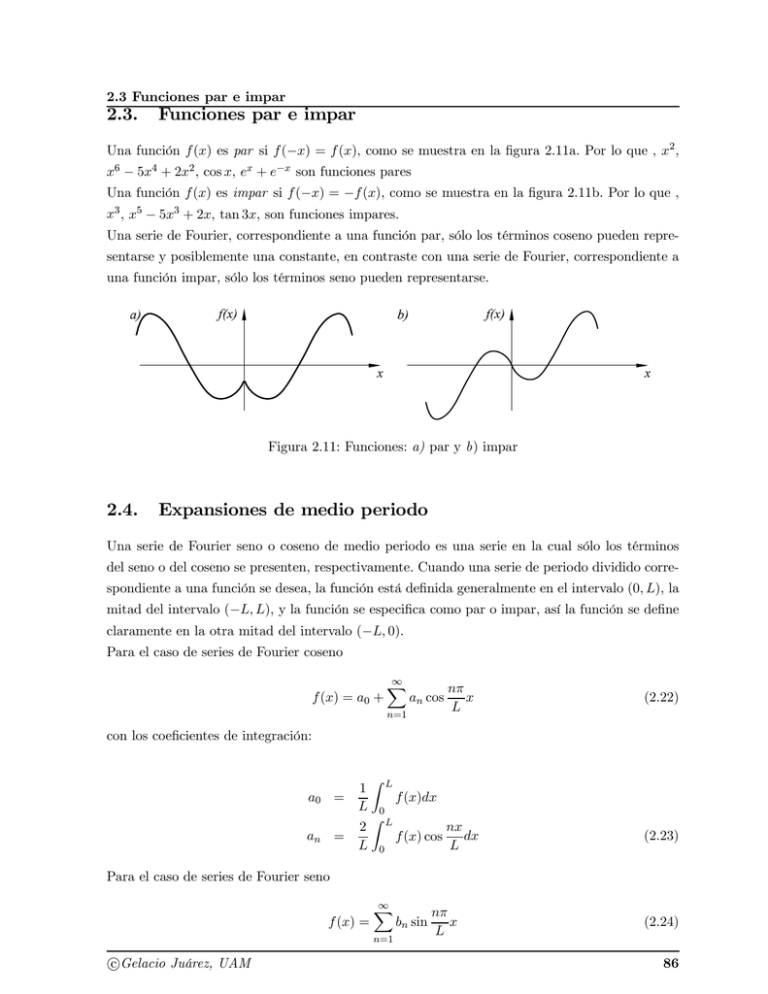
2.3 Funciones par e impar
2.3.
Funciones par e impar
Una función  () es par si  (−) =  () como se muestra en la figura 2.11a. Por lo que , 2 ,
6 − 54 + 22 , cos ,  + − son funciones pares
Una función  () es impar si  (−) = − (), como se muestra en la figura 2.11b. Por lo que ,
3 , 5 − 53 + 2, tan 3, son funciones impares.
Una serie de Fourier, correspondiente a una función par, sólo los términos coseno pueden representarse y posiblemente una constante, en contraste con una serie de Fourier, correspondiente a
una función impar, sólo los términos seno pueden representarse.
Figura 2.11: Funciones: a) par y b) impar
2.4.
Expansiones de medio periodo
Una serie de Fourier seno o coseno de medio periodo es una serie en la cual sólo los términos
del seno o del coseno se presenten, respectivamente. Cuando una serie de periodo dividido correspondiente a una función se desea, la función está definida generalmente en el intervalo (0 ), la
mitad del intervalo (− ), y la función se especifica como par o impar, así la función se define
claramente en la otra mitad del intervalo (− 0).
Para el caso de series de Fourier coseno
 () = 0 +
∞
X
 cos
=1



(2.22)
con los coeficientes de integración:
0 =
 =
Z
1 
 ()
 0
Z
2 


 () cos
 0

(2.23)
Para el caso de series de Fourier seno
 () =
∞
X
=1
c
°Gelacio
Juárez, UAM
 sin



(2.24)
86
2.4 Expansiones de medio periodo
con los coeficientes de integración:
2
 =

Z

 () sin
0



(2.25)
Ejemplo
Determine los coeficientes de Fourier de la función par periódica definida en la ec. (2.26) y
mostrada en la figura 2.12.
 () =
n
25 − 2 −5 ≤  ≤ 5   = 10
(2.26)
Figura 2.12: Función periódica.
Solución. Los coeficientes
1
0 =


Z
0

1
 () =
5
Z
0
5¡
¢
50
25 − 2  =
3
Z
Z
¢

2 

2 5¡
25 − 2 cos
=
 () cos
 =
 =
 0

5 0
5
100
(sin () −  cos )
=
 3 3
100
= − 2 2 cos 
 
(2.27)
(2.28)
(2.29)
 = 0
La correspondiente serie de Fourier es
c
°Gelacio
Juárez, UAM
87
2.4 Expansiones de medio periodo
∞ ³
X
 ´
 =
 () = 0 +
 cos

=1
¶
∞ µ
9 X

100
+

− 2 2 cos  cos
4 =1
 
3
(2.30)
La figura 2.13 muestra la ec. (2.30) cuando  = 4.
f(x) 20
10
-14
-12
-10
-8
-6
-4
-2
0
2
4
6
8
10
12
14
x
Figura 2.13: n=4
Expansión seno
Z
Z
¢
2 5¡
2 


 =

 () sin
25 − 2 sin
 0

5 0
5
´
³ ´
50 ³ 2 2
2 
−
2
sin



+
4
sin
3  3
2
³  ´´
50 ³ 2 2
  + 4 sin2
3  3
2
 =
=
=
(2.31)
La expansión de Fourier seno se obtiene con el coeficiente de las ec. (2.36)
¶
∞ ³
∞ µ
³ ´´
X

50 ³ 2 2
 ´ X
2 
 =
sin

 sin
  + 4 sin
 () =

3  3
2
5
=1
=1
(2.32)
La figura 2.14 muestra la ec. (2.30) cuando  = 4.
f(x)
-14
-12
-10
-8
-6
-4
20
-2
2
4
6
8
10
12
14
x
-20
Figura 2.14: n=8
c
°Gelacio
Juárez, UAM
88
2.4 Expansiones de medio periodo
Ejemplo
Determine los coeficientes de Fourier de la función de medio periodo definida en la ec. (2.33) y
mostrada en la figura 2.15. Realice la expansión coseno y la expansión seno.
n
 () =
 0 ≤  ≤ 3   = 6
(2.33)
Figura 2.15: Expansión de función: a) par y b)impar.
Solución. Los coeficientes para la expansión coseno son
1
0 =

 =
=
=
 =
0

1
 () =
3
Z
3
()  =
0
3
2
Z
2 3


 =
 =
 () cos
 cos

3 0
3
0
´
´
6 ³ ³ 2 ³  ´
2
cos
−
1
−

sin

2  2
2
´
12 ³ 2 ³  ´
cos
−
1
2  2
2
2

Z
Z
2

(2.34)

Z
0

2

 =
 () sin

3
Z
0
3
 sin
(2.35)



6
=
(sin () −  cos )
2
 2
6
= − 2 2  cos 
 
(2.36)
La expansión de Fourier coseno se obtiene con los coeficientes de las ecs. (2.34) y (2.35)
c
°Gelacio
Juárez, UAM
89
2.4 Expansiones de medio periodo
¶
∞ ³
∞ µ
´
X
12 ³ 2 ³  ´
 ´ 3 X

+ = +

 () = 0 +
 cos
cos
− 1 cos

2 =1 2  2
2
3
=1
(2.37)
La expansión de Fourier seno se obtiene con el coeficiente de las ec. (2.36)
¶
∞ ³
∞ µ
X
6
 ´ X

 =

 sin
 () =
− 2 2  cos  sin

 
3
=1
=1
(2.38)
La figura 2.16 muestra la expansión coseno (par) definida en la ec. (2.37) con  = 4, mientras
que la figura 2.17 muestra cuando  = 8.
f(x)
4
2
-8
-6
-4
-2
2
4
6
8
-2
x
-4
Figura 2.16: Expansión coseno, n=4.
f(x)
4
2
-8
-6
-4
-2
2
4
6
-2
8
x
-4
Figura 2.17: Expansión seno, n=4.
Tarea
Determine las series de Fourier de las funciones
 () =
 () =
 () =
n
n
n
 −  −       = 2
2 −       = 2
3 −       = 2
Determine y grafique las series de Fourier coseno y seno de la función
c
°Gelacio
Juárez, UAM
90
2.4 Expansiones de medio periodo
 () =
c
°Gelacio
Juárez, UAM
n
2 0       = 2
91