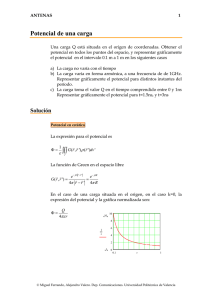
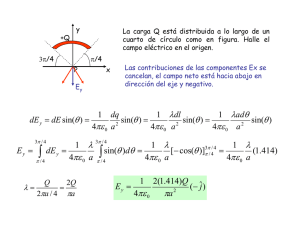
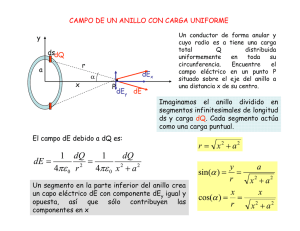
λ λ dl da =

21.94 La carga positiva Q está distribuida uniformemente alrededor de un
semicírculo de radio a. Halle el campo eléctrico (magnitud y dirección) en el
centro de curvatura P.
y
+
+
+
+ +
dEx
dE
+ +
Q
a
θ
P
Consideremos un elemento de longitud dl con
carga dq. El campo dE producido por ese
elemento tiene la dirección del radio del
semicírculo.
dθ
dq dl
+
+
x
Las componentes dEx de todos los elementos
con x < 0 son iguales y opuestas a las
componentes dEx de los elementos con x > 0.
No hay componente neta en x. El campo total
tiene dirección –j.
dEy
a dθ = dl
dq
λ=
dl
La longitud del semicírculo es L=2πa/2
⇒ dq = λdl
dq
1 λdl
1 λa dθ
1 λdθ
dE =
=
=
=
2
2
2
4πε 0 a
4πε 0 a
4πε 0 a
4πε 0 a
1
dE y = dE sin(θ ) =
1
λ sin(θ )dθ
4πε 0
a
π
π
1 λ
1 λ
1 λ
2 λ
π
E y = ∫ dE y =
sin(θ )dθ =
− cos(θ ) 0 =
(1 + 1) =
∫
4πε 0 a 0
4πε 0 a
4πε 0 a
4πε 0 a
0
dq Q
Q
Q
λ=
= =
=
dl L (2πa / 2) πa
r
Ey =
1
2Q ˆ
(− j )
2
4πε 0 πa
Hacia abajo
y
-Q
- - - -
a
P
θ
Carga negativa: dE hacia el elemento dq,
campo neto Ey hacia arriba
dθ
dq
x
y
+Q
La longitud de la distribución de carga es
L=2πa/4 y el campo eléctrico total es:
3π/4
π/4
P
3π / 4
x
Ey =
∫π dE
y
/4
Ey
π/2
+Q
En este caso el campo neto es hacia la
izquierda, las componentes que se
cancelan son las dEy. El campo neto es:
π /2
Ex =
-π/2
∫π dE
− /2
π /2
x
=
∫π dE cos(θ )
− /2
FLUJO DEL CAMPO ELECTRICO (CAP. 22)
Cálculos de campo eléctrico
Dada una distribución de
carga, ¿cuál es el campo
eléctrico que produce esa
distribución en un punto P?
?
Si se conoce la disposición del
campo eléctrico en una región,
¿qué se puede saber acerca de la
distribución de carga en esta
región?
Consideremos una caja cerrada que puede
contener o no contener carga eléctrica hecha
de un material que no influye en los campos
eléctrico (superficie imaginaria).
¿Cómo se puede saber cuánta carga hay dentro
la caja?
E
E
+ +q
a
+q +
+q
E
+
b
-
c
Si movemos una carga de prueba q0 en torno a las proximidades de la caja y
medimos la fuerza F que la carga experimenta en distinta posiciones
podemos elaborar un mapa tridimensional del campo eléctrico E=F/q0
afuera de la caja y hallar el valor de la carga puntual en el interior de la
caja.
Para conocer el contenido de la caja es necesario medir E sólo en la
SUPERFICIE de la caja.
Se puede decir que en los casos a y b de la figura hay un * FLUJO
ELECTRICO saliente, en el caso c de carga negativa un FLUJO
ENTRANTE.
* En analogía con los vectores de velocidad de un fluido en movimiento, pese a que
un campo eléctrico no “fluye” en realidad.
E=0
E=-E
+σ
-
+
q=0
Si no hay carga en la caja
el campo eléctrico es 0,
no hay flujo a través de
la caja
El campo eléctrico fluye
hacia adentro en la mitad
y fluye hacia afuera en la
otra mitad. El flujo neto
es 0
Hay carga afuera de la
caja. En un extremo de la
caja el campo fluye hacia
adentro y en el otro
extremo hacia afuera. El
flujo neto es 0
Hay una relación entre el signo (positivo, negativo, cero) de la carga neta en
la caja cerrada y el sentido (saliente, entrante, cero) del flujo eléctrico neto
a través de la superficie de la caja. También hay una relación entre la
magnitud de la carga adentro de la caja y la intensidad del flujo eléctrico.
El flujo eléctrico neto a través de la superficie de la caja es directamente
proporcional a la magnitud de la carga neta que encierra la caja.
E
CALCULO DEL FLUJO ELECTRICO ΦE
r
A = Anˆ
Consideremos una superficie
n̂ φ=0
de área
A y un campo eléctrico uniforme.
De forma aproximada, podemos exprimir ΦE
en términos de las líneas de campo que pasan
a través de A. Aumentar el área significa
que más líneas atraviesan A y el flujo
aumenta.
A
E
n̂
n̂ φ
A
E
n̂
φ=90ο
Si el área es plana pero no perpendicular al
campo eléctrico, menos líneas la atraviesan.
En ese caso consideramos el área reducida
Acosφ.
Si el área es paralela al campo eléctrico,
las líneas no la atraviesan.
E
r
A = Anˆ
n̂
r
A
A
r r
Φ E = E ⋅ A = EA cos(ϕ )
Producto escalar
[ m 2 ]
ΦE =
[C ]
E
r
A
Flujo hacia afuera: ΦE positivo
cosφ=1
E
r
A
Flujo hacia adentro: ΦE negativo
cosφ=-1
Si el campo eléctrico no es uniforme, o si la superficie no es plana, se divide el
área en muchos elementos pequeños dA, cada uno de los cuales tiene su vector
unitario:
r
dA = dAnˆ
r r
Φ E = ∫ E cos(ϕ )dA = ∫ E ⋅ dA
22.1 FLUJO ELECTRICO A TRAVES DE UN DISCO
Un disco cuyo radio mide 0.1 m está orientado con
su vector unitario normal formando un ángulo de
30o respecto a un campo eléctrico uniforme de
magnitud 2 103 N/C. ¿ Cuál es el flujo eléctrico a
través del disco? ¿Cuál es el flujo si se orienta el
disco de modo que su normal sea perpendicular a
E? ¿Cuál es el flujo si la normal del disco es
paralela a E?
E
n̂
30o
A
A = πR 2 = π (0.1 m 2 ) = 0.0314 m 2
m 2
Φ E = EA cos(30 ) = (2 10 / C )(0.0314 m ) cos(30) = 54
C
o
3
2
Φ E = EA cos(90) = 0
=0
2
m
Φ E = EA cos(0) = (2 103 / C )(0.0314 m 2 ) = 63
C
=1
22.1 FLUJO ELECTRICO A TRAVES DE UNA ESFERA
n̂
E
q
Una carga puntual q=3 µC está rodeada por una
esfera centrada en la carga y cuyo radio es
R=0.2 m. Halle el flujo eléctrico a través de la
esfera debido a esta carga.
El campo eléctrico es el campo de una carga
puntual. Nos interesa el flujo a través de la
superficie de la esfera, que está a una
distancia R de la carga:
2
q
3 10 −6 C
9 m
5
=
=
/C
E=
6
.
75
10
(
8
.
9
10
)
2
2
2
C
(0.2m)
4πε 0 R
1
La superficie de la esfera es curva, el campo eléctrico E es igual en cada
punto de la superficie y es paralelo al vector normal a la superficie:
Φ E = ∫ EdA = E ∫ dA = E (4πR 2 )
2
m
Φ E = (6.75 105 / C )(4π )(0.2m) 2 = 3.4 105
C
π/2
-Q
-π/2
La carga negativa Q = -10 nC está distribuida
uniformemente sobre un círculo de radio
a=0.005 m como en figura. Halle la magnitud y
la dirección del campo eléctrico en la origen
del sistema de coordenadas.