Solucions a “Ejercicis i problemes”

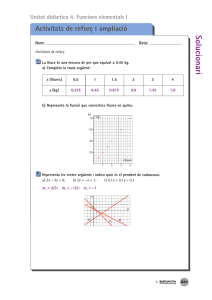
5
Solucions a “Ejercicis i problemes”
PÀGINA 116
38
Pàg. 1
Roser ha comprat un regal d’aniversari per a Pau que ha costat 100 €. La resta
dels amics del grup decidix pagar el regal entre tots. Construïx una funció que ens
done els diners que ha de posar cada un depenent del nombre de persones que hi
haja i dibuixa-la.
Si van a sopar a un restaurant en què el menjar val 10 €, quina serà la funció dels
diners que ha de posar cada un, sense incloure Pau, depenent del nombre de persones que són? Dibuixa-la en els mateixos eixos. Digues el domini de definició
d’ambdues funcions tenint en compte que x només pren valors naturals i suposant
que el nombre d’amics no supera 10.
Si el número de amigos es x, x é N, la función que
da lo que debe pagar cada uno es y1 = 100 .
x
Si van a un restaurante, entonces la función es y2 = 100 + 10(x + 1) .
x
El dominio de definición de ambas funciones es Dom = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
39
Y
120
100
y1
y2
10
1
10 X
El metge ha posat a Ricard un règim d’aprimament de 12 setmanes i li ha fet
aquest gràfic per a explicar-li el que espera aconseguir:
PES (en kg)
a)Quin n’era el pes en començar el règim?
80
b)Quant ha d’aprimar-se per setmana en la primera
70
etapa del règim? I entre la 6a i la 8a setmana?
60
c)Troba l’expressió analítica d’aquesta funció.
a)Ricardo pesaba 80 kg al comenzar el régimen.
b)5 = 1,67 kg por semana.
3
Entre la sexta y octava semana no tiene que adelgazar nada.
SETMANES
1 2 3 4 5 6 7 8 9 10 11 12
c)Buscamos la ecuación de cada uno de los tramos:
•Para 0 Ì x Ì 6, la pendiente m = – 10 = – 5 y n = 80 8 y = – 5 x + 80
6
3
3
•Para 6 < x Ì 8, y = 70
•Para 8 < x Ì 12, m = – 5 y pasa por (12, 65)
4
y – 65 = – 5 (x – 12) 8 y = – 5 x + 80
4
4
Luego, la expresión analítica de esta función será:
°– 5 x + 80
§ 3
y = ¢70
§ 5
£– 4 x + 80
Unitat 5. Funcions elementals
si 0 Ì x Ì 6
si 6 < x Ì 8
si 8 < x Ì 12
5
Solucions a “Ejercicis i problemes”
40
Les despeses anuals, en euros, d’una empresa per la fabricació de x ordinadors
són: G(x) = 20000 + 250x
I els ingressos, en euros, que s’obtenen per les vendes són: I(x) = 600x – 0,1x 2
Quants ordinadors s’han de fabricar perquè el benefici (ingressos menys despeses)
siga màxim?
La función beneficio es:
B = I – G = 600x – 0,1x 2 – (20 000 + 250x) 8 B(x) = –0,1x 2 + 350x – 20 000
El vértice es el máximo: V = –350 = 1 750
–2 · 0,1
Se deben fabricar 1 750 ordenadores para que el beneficio sea máximo.
41
En el contracte de treball d’un empleat figura que el seu sou pujarà un 8%
anual. El seu sou inicial és de 24 000 euros anuals.
a)Escriu la funció que relacione els diners que guanya amb el nombre d’anys transcorreguts.
b)Quant guanyarà d’ací a 10 anys?
a)C = 24 000 · 1,08 t
b)C (10) = 24 000 · 1,0810 = 24 000 · 2,1589 = 51 814 €
■Problemes “+”
42
L’altura, h, a la qual es troba en cada instant, t, una pedra que llancem verticalment cap amunt amb una velocitat de 20 m/s és h = 20t – 5t 2.
a)Representa gràficament la funció.
b)Digues quin n’és el domini de definició.
c)En quin moment aconseguix l’altura màxima? Quina és aquesta altura?
d)En quin moment cau la pedra al sòl?
e)En quin interval de temps la pedra està a una altura superior a 15 metres?
a)
b)Dominio de definición = [0, 4]
c)La piedra alcanza la altura máxima a los 2 segundos
de haberla lanzado, y es de 20 m.
Y
20
d)A los 4 segundos.
e)20t – 5t 2 = 15
15
5t 2 – 20t + 15 = 0
10
t=1
t=3
2
–5t + 20t – 15 Ó 0 8 1 Ì t Ì 3
t 2 – 4t + 3 = 0
2
Unitat 5. Funcions elementals
4
X
Pàg. 2
5
Solucions a “Ejercicis i problemes”
43
Tenim 200 kg de taronges que hui es vendrien a 0,40 €/kg. Cada dia que passa se n’spatla 1 kg i el preu augmenta 0,01 €/kg.
Quan hem de vendre les taronges per a obtindre-hi el màxim benefici? Quin serà
aquest benefici?
Sea t el tiempo, en días.
La función que da el precio de las naranjas según transcurren los días es (kilos de naranjas Ò precio de cada kilo):
P (t ) = (200 – t )(0,40 + 0,01t )
P (t ) = 80 + 2t – 0,40t – 0,01t 2 = –0,01t 2 + 1,60t + 80
El máximo de la función está en el punto de abscisa: –b = –1,60 = 80
2a –0,02
Las naranjas se deben vender, para obtener el máximo beneficio, dentro de 80 días, y se
venderán por 144 euros.
44
El cost per unitat de fabricació de certs sobres disminuïx segons el nombre
d’unitats fabricades i ve donat per la funció:
y = 0,3x + 1 000
x
a)Quins valors pren la variable independent, x ?
b)Calcula el cost per unitat i el cost total per a 10 sobres. Fes el mateix per a 100 000
sobres.
c)A quant creus que s’acosta el cost per unitat quan el nombre de sobres es fa molt
gran?
a)x toma valores naturales.
b)•Para 10 sobres:
Coste por unidad = 1 003 = 100,3
10
Coste total de 10 unidades = 1 003
•Para 100 000 sobres:
Coste por unidad = 30 000 + 1 000 = 0,31
100 000
Coste total de 100 000 unidades = 31 000
c)El coste por unidad se acerca a 0,3.
45
En una piscina hi ha un trampolí a 8 m de l’aigua. Llancem una pilota rodant i cau a l’aigua a 12 m del trampolí. Escriu l’equació de la trajectòria descrita
per la pilota des que ix del trampolí fins que toca l’aigua. Dóna’n el domini de
definició.
☞ La trajectòria és una paràbola y = ax2 + bx + c amb el
seu vèrtex en el punt de caiguda. Pren O com a centre de
coordenades i tin en compte que el vèrtex és (0, 8).
8m
O
Unitat 5. Funcions elementals
12 m
Pàg. 3
5
Solucions a “Ejercicis i problemes”
resolución 1
Pàg. 4
(0, 8)
O
Tomando el centro de coordenadas en el punto O, el
vértice de la parábola es (0, 8). La ecuación de la parábola queda así:
(12, 0)
y = ax 2 + b
°
2
¢ y = ax + 8
Para x = 0, y = 8 8 8 = b £
Calculamos el valor de a sabiendo que pasa por (12, 0):
0 = a · 122 + 8 8 a = – 8 = – 1
144
18
La ecuación de la trayectoria es y = – 1 x 2 + 8, definida en [0, 12].
18
resolución 2
En la resolución anterior se ha tenido en cuenta que la trayectoria es una parábola con su
vértice en el punto de caída. Resolvámoslo, ahora, como lo haría un físico, teniendo en
cuenta, solamente, las leyes del movimiento:
Tiempo que tarda en caer 8 m: (movimiento uniformemente acelerado. Aceleración, g):
√
1 gt 2 = 8. Tomamos g = 10 m/s2 8 5t 2 = 8 8 t = 8
2
5
¿A qué velocidad rueda la pelota por el trampolín? Tengamos en cuenta que, a esa veloci-
√ 85 s (componente horizontal).
Movimiento uniforme e = v · t 8 12 = v · √ 8 8 v = 12
5
√8/5
dad, recorre 12 m en
Obtengamos la ecuación de la trayectoria tomando O como origen de coordenadas:
8/5 2 1 2
√8/5x
2
Comp. horizontal: x = 12 t °§ t = 12 8 t = 144 x = 90 x √8/5 ¢
§
Comp. vertical: y = 8 – 5t 2 £ y = 8 – 5 · 1 x 2 = 8 – 1 x 2
90
18
Hemos obtenido la trayectoria y = 8 – 1 x 2, la misma que antes como es natural.
18
Unitat 5. Funcions elementals