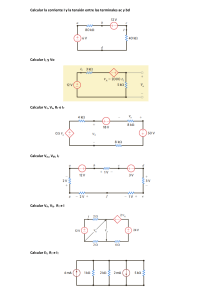
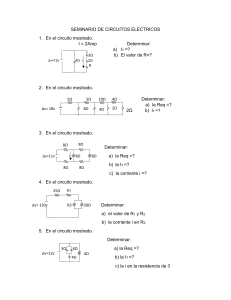
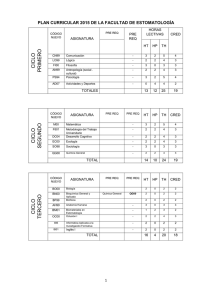
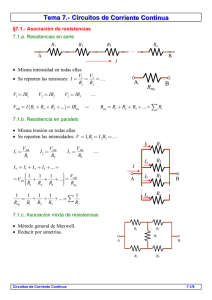
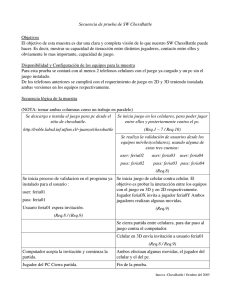
En el circuito de la figura a) Calcular la intensidad que circula por
Anuncio

En el circuito de la figura a) Calcular la intensidad que circula por cada resistencia b) Calcular la diferencia de potencial entre los puntos A y B, y entre C y B c) Comprobar que la potencia suministrada al circuito es igual a la potencia consumida y calcular el rendimiento del motor A R1=6Ω ε1=10 V ε2=42 V r2=1Ω r2=1Ω i2 i1 R2=6Ω R3=4Ω R4=10 Ω i3 B C R5=10 Ω Resolución a) Asignamos sentidos arbitrarios a las corrientes del circuito A R1=6Ω ε1=10 V ε2=42 V r2=1Ω r2=1Ω R2=6Ω R3=4Ω i2 i1 B R4=10 Ω i3 C R5=10 Ω La resistencia equivalente de R4 y R5 es Req=5Ω por estar asociadas en paralelo. En el nudo B i1+i3=i2 En la malla izquierda 13i1+i2=42-10=32 En la malla derecha 9i3+i2=42 La resolución del sistema de ecuaciones proporciona i1=2A, i2=6A, i3=4A. b) La diferencia de potencial entre A y B es V A − VB = r (−i2 ) − (−ε 2 ) = −6 + 42 = 36V y entre C y D VC − V D = Req i3 = 20V c) La energía es suministrada por el generador de ε2=42 V, y la potencia que suministra es Psum = 42V ·6 A = 252W La potencia consumida es Pcos n = ε 1i1 + ( R1 + r1 + R2 )i12 + r2 i22 + ( R3 + Req )i32 = 252W