Sobre una mesa horizontal hay dos masas m y m/2, que pueden

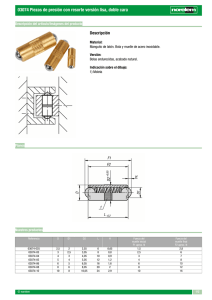
Sobre una mesa horizontal hay dos
masas m y m/2, que pueden
considerarse puntuales, situadas como
se indica en la figura. La masa m está
unida a la mesa por un muelle de
constante k y de longitud natural L/2.
Y
L/2
k
L/2
m
m/2
H
X
Mediante la masa m se comprime
el muelle una longitud L/4 y se
suelta en el instante t0=0. El
rozamiento entre la masa m y la
mesa es despreciable.
Al cabo de un tiempo t1 se rompe el muelle y simultáneamente aparece rozamiento entre
la masa y la mesa.
Utilizando los ejes dibujados, calcular:
1)
Ecuación del movimiento de la masa m hasta que se rompe el muelle.
2)
Velocidad y aceleración de m en el instante t1.
3)
Cuantos periodos y fracciones de periodo del movimiento de m han ocurrido
desde t0 hasta t1.
4)
Valor máximo que puede tener el coeficiente de rozamiento µ para que las
masas choquen.
5)
Suponiendo µ=0, lugar del suelo (plano y=0) donde cae la masa m/2, sabiendo
que el choque entre las masas es elástico.
DATOS:
m = 250 g
L=2m
tómese g = 10 m/s2
H = 80 cm
k = 81 N/m
t1 = π/4 s
NOTA:
Resolver simbólicamente y después hacer aplicación numérica.