1ºB/C - 10-may-2010 - IES Medina Albaida
Anuncio

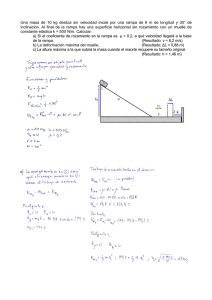
EXAMEN DEL TEMA 4 LA ENERGÍA Y SU TRANSFERENCIA EXAMEN DEL TEMA 4 LA ENERGÍA Y SU TRANSFERENCIA Páginas 110-157 del libro de texto Páginas 110-157 del libro de texto Recuperación de 1ºB/C de Bachillerato - Lunes, 10 de mayo de 2010 Se pide: * claridad en la exposición, sin omitir explicaciones * limpieza y orden en cada pregunta, cuestión, ejercicio o problema * adaptar la respuesta en cada caso al enunciado propuesto * utilizar las unidades adecuadas * cuidar la ortografía * utiliza g = 10 m/s2 1.- Un automóvil circula a 108 km/h. Su motor desarrolla una fuerza útil de 1.000 N. 1a) ¿cuál es la potencia útil del motor en kW y en CV?, 1b) ¿qué trabajo desarrolla si recorre 20 km a esa velocidad? 2.- Desde una terraza situada a 20 m de altura se lanza una pelota de 50 g formando un ángulo de 60º con la horizontal y a una velocidad de 20 m/s. Calcula razonadamente: 2a) la energía mecánica inicial de la pelota, 2b) la velocidad de la pelota cuando se encuentra a 5 m sobre el suelo, 3.- Lanzamos un objeto de 500 g de masa a 10 m/s sobre una superficie horizontal, sin rozamiento, contra un muelle situado horizontalmente. La máxima compresión que experimenta el muelle es de 10 cm. Calcula razonándolo: 3b) el trabajo necesario para comprimirlo 10 cm desde su posición de equilibrio, 3a) la constante recuperadora elástica del muelle en unidades S.I. 4.- Un cuerpo de 1 kg de masa se encuentra en reposo sobre un plano horizontal. El coeficiente dinámico de rozamiento entre el cuerpo y el plano vale 0’6. Se aplica al cuerpo una fuerza horizontal de 10 N. Deduce razonadamente: 4a) la fuerza útil que acelera el cuerpo, 4b) la velocidad que llevará el cuerpo tras recorrer 20 m sobre el plano. 5.- A un calorímetro que contiene 100 g de agua a 19 ºC le añadimos un bloque metálico de una determinada aleación de 50 g de masa y calentado a 100 ºC. La temperatura de equilibrio es de 20 ºC. Sabiendo que el calor específico del agua es de 4’18 J/g.K y suponiendo que no hay pérdidas de energía, deduce razonándolo: 5a) el aumento de energía interna experimentado por el agua, 5b) el calor específico de la citada aleación, expresado en unidades S.I. 6.- Se deja caer por un plano inclinado 30º sobre la horizontal un cuerpo de 2 kg de masa. El coeficiente dinámico de rozamiento entre cuerpo y plano es 0’2, deduce razonándolo: 6a) el trabajo de las fuerzas de rozamiento si la longitud del plano es de 2 m, 6b) la velocidad final que lleva el cuerpo al terminar de deslizar sobre el plano. 7.- Una grúa realiza un trabajo de 60 kJ para elevar un peso de 500 kg a 10 m en 50 s. Teniendo en cuenta la existencia de rozamiento, calcula de forma razonada: 7a) la potencia total desarrollada por la grúa, 7b) el trabajo útil desarrollado por la misma. 8.- Se lanza una bala de 10 g de masa a 400 m/s contra un bloque de madera que está fijo y penetra en el mismo una distancia de 50 cm hasta pararse. Calcula razonadamente: 8a) el trabajo realizado por la fuerza que se opone a la penetración de la bala, 8b) el valor de dicha fuerza en unidades S.I. Recuperación de 1ºB/C de Bachillerato - Lunes, 10 de mayo de 2010 SOLUCIONES: 1a) La velocidad de 108 km/h equivale a 108/3’6 m/s = 30 m/s. La potencia útil será igual al producto de la fuerza útil por la velocidad: P = F.v = 1.000*30 W = 30.000 W = 30 kW. La potencia expresada en CV es aproximadamente: P = 30.000/735 CV = 40’8 CV. 1b) El trabajo realizado será el producto de la fuerza útil por el desplazamiento, ya que ambos tienen en todo instante la misma dirección y sentido, ya que la fuerza útil contrarresta en todo momento a la fuerza de rozamiento total: W = F.x = 1.000*20.000 N.m = 2.107 J = 20 MJ. 2a) En el instante inicial tiene energía potencial porque hay altura: Ep = m.g.h = 0’05*10*20 J = 10 J. También tiene energía cinética porque lleva velocidad: Ec = ½.m.v2 = 0’5*0’05*(20)2 J = 10 J. La energía mecánica inicial era: Em = Ep + Ec = 20 J. (No importa el ángulo de lanzamiento) 2b) Cuando esté a 5 m sobre el suelo su Ep = m.g.h = 0’05*10*5 J = 2’5 J. Como la Em se conserva si despreciamos el rozamiento: Ec = Em – Ep = (20-2’5) J = 17’5 J. De aquí deducimos el valor de la velocidad: ½.m.v2 = 17’5 v2 = 17’5*2/0’05 = 700 m2/s2 v = 26’5 m/s más o menos. 3a) El trabajo necesario para comprimir el muelle será igual a la disminución de la Ec del objeto y se acumula en el muelle en forma de Ep elástica, luego: W = ½.m.v2 = 0’5*0’5*(10)2 = 25 J. 3b) Como la Ep elástica del muelle vale: Ep = ½.k.x2 y como sabemos que el muelle se ha comprimido un máximo de 10 cm (= 0’1 m), se deduce que la constante recuperadora elástica del muelle vale: k = 2.Ep/x2 = 2*25/(0’1)2 N/m = 5.000 N/m. 4a) La reacción normal del plano vale 10 N y la fuerza de rozamiento es: FR = µ.N = 0’6*10 N = 6 N. Por tanto, la fuerza útil que acelera el cuerpo es: Fútil = FT – FR = (10-6) N = 4 N. 4b) La aceleración con que se mueve el cuerpo es: a = Fútil/m = 4/1 N/kg = 4 m/s2. Como lleva un MRUA con vo = 0, el espacio recorrido es: x = ½.a.t2 t2 = 2.x/a = 2*20/4 s2 = 10 s2. El tiempo que le cuesta recorrer los 20 m fue: t = (10)½ s = 3’16 s, y la velocidad que llevará en ese instante con MRUA es: v = vo + a.t = 0 + 4*3’16 m/s = 12’64 m/s aproximadamente. 5a) Para calcular el aumento de energía interna experimentado por el agua al calentarse empleamos la masa en g porque c viene en J/g.K, luego: ∆Ei = m.c.∆T = 100*4’18*(20-19) J = 418 J. 5b) La misma variación de energía interna disminuye en el bloque metálico: ∆Ei = mb.cb.∆Tb. La disminución de temperatura del bloque ha sido 80 ºC = 80 K, el calor específico de la aleación es: cb = ∆Ei/mb.∆Tb = 418/(50*80) J/g.K = 0’1045 J/g.K y en unidades S.I. es: 104’5 J/kg.K. 6a) La componente del peso perpendicular al plano es: py = m.g.cos(30º) = 2*10*0’866 N = 17’32 N. La normal es igual y contraria y la fuerza de rozamiento vale: FR = µ.N = 0’2*17’32 N = 3’464 N. Como la fuerza de rozamiento y el desplazamiento llevan sentidos contrarios, el trabajo de rozamiento es negativo: WR = FR.x.cos(180º) = - 3’464*2 N.m = - 6’928 J. 6b) Al estar inclinado 30º, la h máxima es: h = x.sen(30º) = 2*0’5 m = 1 m Ep = m.g.h = 2*10*1 J = 20 J. La Ec abajo es igual a la Ep arriba más el trabajo de la FR Ec = Ep + WR = (20 – 6’928) J = 13’072 J = ½.m.v2 v2 = 13’072*2/1 = 26’144 v = (26’144)½ m/s = 5’11 m/s. 7a) La potencia total es el cociente entre el trabajo realizado y el tiempo empleado, o sea: PT = W/t = 60.000/50 J/s = 1.200 W = 1’2 kW. 7b) El W útil es igual a la variación de la Ep gravitatoria del cuerpo: Wútil = ∆Ep = m.g.h = 500*10*50 J = 500*10*10/50 W = 50.000 J = 50 kJ. 8a) El trabajo realizado por la FR que se opone a la penetración de la bala es igual y de signo contrario a la variación de la Ec de la misma: WR = - ∆Ec = - ½.m.v2 = - 0’5*0’01*(400)2 J = - 800 J. 8b) Ese trabajo es igual a la fuerza que se opone a la penetración por el desplazamiento realizado y ambas magnitudes tienen sentidos opuestos: WR = - FR.∆x FR = - WR/∆x = - (-800/0’5) J/m = 1.600 N. (Si el desplazamiento fuera en el sentido positivo del eje x: ∆x = + 0’5.i (m), entonces el vector fuerza iría en sentido opuesto: FR = - 1.600 i (N).