1.1.16.5 Distancia entre dos puntos. La circunferencia

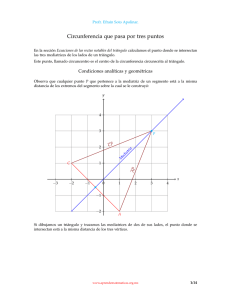
1.1.16.5 Distancia entre dos puntos. La circunferencia
Considérense, en el plano cartesiano, dos puntos: P( x1 , y1 ) y Q( x 2 , y 2 ) .
En el caso en que x1 < x 2
A( x1 , y 2 ) . Véase la figura
y
y1 < y 2 ,
puede construirse el triángulo
PAQ,
con
El triángulo PAQ es rectángulo, con PQ como hipotenusa.
La distancia entre P y Q es la longitud de PQ . El Teorema de Pitágoras lleva a:
d ( P , Q ) = ( x1 − x 2 ) 2 + ( y 1 − y 2 ) 2
Es fácil probar que esta fórmula es válida con independencia de las relaciones entre x1 y
x2 y entre y1 y y2.
Ejemplo:
Calcúlese la distancia entre los puntos A(−1,2) y (3,2) .
Solución
Considérese un punto C (h, k ) y un real positivo r.
El conjunto de los puntos del plano cuya distancia a C es r se denomina circunferencia
de centro C y radio r.
Sea P( x, y ) un punto cualquiera de la circunferencia.
Así, d ( P, C ) = r
Es decir,
( x − h) 2 + ( y − k ) 2 = r
De esta ecuación se obtiene:
(x − h )2 + ( y − k )2
= r2
Esta última, se conoce como ecuación de la circunferencia de centro C y radio r.
Ejemplo:
Encuéntrese la ecuación de la circunferencia que pasa por
C (−2,−3) .
A(3,−1)
y tiene centro
Solución (Véase la figura )
El cuadrado del radio es:
r 2 = (3 − (− 2)) + (− 3 − (− 1))
r 2 = 29
2
2
La ecuación de la circunferencia es:
(x + 2)2 + ( y + 3)2 = 29
Ejercicio:
Encuéntrese la ecuación de la circunferencia que pasa por los puntos:
y C (1,7)
Respuesta:
(x + 2)2 + ( y − 3)2 = 25
A(−2,8) ,
B(3,3)