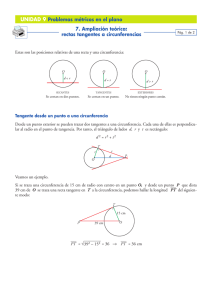
Ejercicios de tangencias

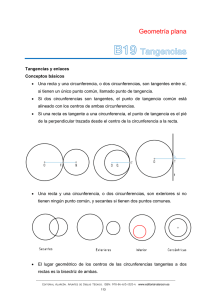
Unarectay unacircunferencia,
o doscircunferencias,
sontangentes
entresí, si tienenun únicopuntocomún,
lamadopuntode tangencia.
Unarectay unacircunferencia,
o doscircunferencias,
sonexteriores
si no tienenningúnpuntocomún,
y secantes
si tienendospuntoscomunes.
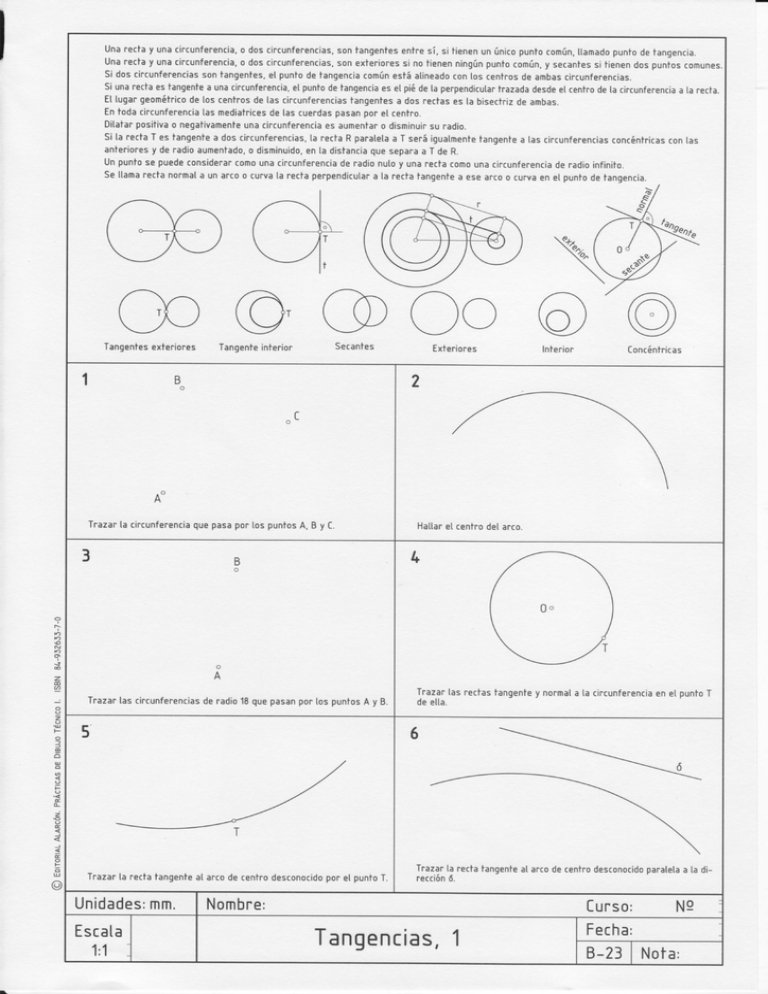
Si doscircunferencias
sontangentes,
el puntode tangencia
común
estáatineado
conlos centrosde ambascircunferencias.
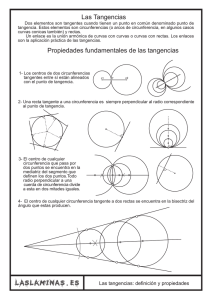
Si unarectaes tangente
a unacircunferencia,
e[ puntodetangencia
es el piéde[a perpendicutar
trazadadesdeel centrode la circunferencia
a [a recta.
E[tugargeométrico
de toscentrosde tascircunferencias
tangentes
a dosrectases [a bisectriz
de ambas.
Entodacircunferencia
las mediatrices
de tascuerdaspasanpor et centro.
Dilatarpositiva
o negativamente
unacircunferencia
es aumentar
o disminuir
su radio.
Si la rectaT es tangente
a dosci¡cunferencias,
la rectaR paratela
a T seráiguatmente
tangente
a las circunferencias
concéntricas
conlas
y de radioaumentado,
anteriores
o disminuido,
queseparaa T de R.
en la distancia
Unpuntose puedeconsiderar
comounacircunferencia
de radionuloy unarectacomounacircunferencia
de radioinfinito.
Se llamarectanormala un arcoo curva[a recfaperpendicular
a la rectatangente
a esearcoo curvaen el puntode tangencia.
Tangentes
exteriores
Tangente
interior
Secantes
Exteriores
Interior
Concéntricas
2
Bo
A"
Trazarta circunferencia
quepasapor [ospunfosA, B y C.
3
Hattarel centno
delarco.
4
o
r\
¡o
¡r)
o
N¡
¡r,
o
I
I
.¡
ó
I
o
A
z
.T¡
2
j
o
(J
Trazar
lascircunferencias
deradio18quepasan
porlospuntos
A y B.
Trazarlas rectastangente
y normala la circunferencia
en el puntoT
de ella.
=
o
¡t¡t
F
-)
:)
o
5
6
g
o
ó
U
u,
9
F
(J
É.
¿
.o
L
(J
e.
J
J
c.
o
E
ct
Lu
@
Trazar[a rectatangentea[ arcode centrodesconocido
por el puntoT.
Unidades
m :m .
E s c ala
1: 1
Trazarla rectatangente
al arcode centrodesconocido
paralela
a la dirección
6.
N o mrbe :
T a n g e n c i a1s ,
fu r so :
F e ch a :
Ng
B-23| Nota:
2
A
Traza¡un¿(¡acunfeaeñcia
de 18nrnde r¿dioquepesepo¡ el puntoA
y tengasu centloen [a re(t¡ R.
Trazaruñ¿circunferc¡(i¿
qle p¿sepor los puntosA y B y ieñg¿su
centroen l¿ ¡ectáR.
4
lrazar un¿carcunfe¡enc¡a
de 18mr¡de fad¡o.t¿ngentea l¡ ¡ecteS y
queleñg¿su cpntroen l¿ aect¿R.
Tfez¿run¿circunfercncia
de 1ónn de a¿dio.
t¡ñoente¿ la cif(unferen(i¡O y queteñg¿su centroen le reclaR.
7
Tr¿z¿a
dos(iÍcunfefen(ias
t¿ngentes
a tásrc(tásS y T queteng¿nsu
centrosobre[¿ rcct¡ R.
q
6
e
Ta¡z¿rdosc¡¡cunfeaencias
tangentes
¿ l¿sd¿d¿sd€ iguálredio,que
lenqansu centroen l¿ aectaR,
Trazerdos(iacunferenc¡as
tangentes
a l¿ d¿d¿cuyocentrose en(uentreen [¿ rc(t¿ R y p¿señpoaP.
Unidadem
s :m . Nombre:
EscaIa
1:1
Ta n g e n c i a2s ,
Cu r so : N q
F e ch a :
B- 2 l*| N ota:
6
3
a
I
¡
¡
9
¡
I
!
I
@
Unidades.mm.
Nombrer
Esc¿l¿
1;1
Curso: N9
T angencias,3
B-25 Nota:
Po
P
Tr¿z¿rdos circunferencias
de 14mmde radio,quepasenpor P y sean
tangentesa la de centro0.
3
4
Trazardos circunferencias
de 10mmde ¡adiotangentesa las dadas.
o
F
Trazarun¿ci¡cunferencia
de 21mmde r¿dio,quepasepor P y sea
tangente
a R.
5
Traza¡unacircunferencia
de 30 mmde radiotangente
a las dadas,
exteriorde 0 e incluyente
de 0.
6
o
N
a
o
€
-t
z
o
o
2
ru
F
o
e
o
U
o
9
É
€¿
L
E
I
d
L
U
Trazarunacircunferencia
de 44 mmde radio,tangenteen su interior
a las dadas.
U nidades
m :m .
E s c ala
1: 1
Trazar dos circunferenciastangentes a R y a la dada en el punto T,
Nombre:
l*
Tangencias,
Cu r so :
F e ch a :
N9
8-26| Nota:
2
Trazardoscircunferencias
de 14mmde radio,tangentes
a la daday
a [a rectaR.
Trazarunacircunfe¡encia
de 50 mmde radio,tangentea ta rectaR y
a t¿ dadaen su interior.
3
Circunsoibir
un triánguloequitátero
a la circunferencia.
Trazarunacircunferenci¿
tangentea tas rectasR, S y T
T¡azartas circunferencias
de radio15tangentesa las rectasR y S.
Trazarseiscircunferencias
langentesentresí y a ta dadainteriormente.
ts
D
a
€
o
-t
o
z
@
I
j
=
F
g
o
ó
9
É
¿
a
e
)
J
e
tr
U
o
Unidades:
mm. Nombre:
Es c ala
1: 1
T a n g e n c i a s ,5
Cu r so :
F e ch a :
N9
B-21| Nota:
Tr¿zarlas ci¡cunferencias
concéntricas
tangentes
a ires dadasde
igualradio.
3
Trazartascircunfe¡encias
tangentes
a las de centro0 y 0 dadoel
puntode tangencia
T en unade ellas.
4
lrA
Trazarunarectatangenteinterior,comúna las dos circunferencias.
5
N
D
o
N
o
o
z
o
I
o
!¿
z
!u
F
3
e
u
9
F
e
L
€¿
e
-=
6
U
@
Trazarunarectatangente
exterior.común
a las doscircunferencias.
Unidades:
m m . Nombre:
Es c ala
1: 1
Trazardos ci¡cunferencias
tangentesa la daday a [a recfaR, dadoel
puntode tangencia
T en la rect¿.
T a n g e n c i a6s,
Cu r so :
F e ch a :
N9
Dilatación
B-28| N ota:
quemedianle
Enlacees un arcode circunferencia
tangencias
unedos ¡ectas,unarectay un alco o dos a¡cos.
2
oE
lospuntos
mediante
tangentes
entresí.
Enlazar
arcosdecircunferencia
T
Enlazarlas dos rectasconun afco.Se conoceet puntode tangencia
en la rectaR.Dossoluciones.
3
4
s
Enlazarlas dos rectasconun afcode radio23 mm.
Enlazarla rectaS conel arcoA condos arcosde r¿dio19mm,uno
de ellosinterior,el otro exte¡iora[ arco.
5
6
o
F
n
€
N
o
{
o
z
o
I
J
o
z
U
F
o
3
E
6
U
ó
I
F
Qo
c
c
€¿
0"
e
I
J
f
e
o
=
ó
U
Enlaza¡los dos ¿rcosd¿dosconotro de radio25 mm.
Enlazerlos dos a¡cosdadosconotro de radio11mm.
@
Unidades:
mm. Nombre:
Escala
1:1
Tangencias,
?
Enlaces
Cu r so :
F e ch a :
N9
B-29| Nota:
El óvaloes unacuruacerraday planafornadapor arcosde circunferencia
y simétricarespectode dos ejes perpendicutares.
E[ovoidees unacurvacerraday planaformadapof afcosde circunferencia
y simétricarespectode un eje.
2
D
Const¡uirel óvaloconocido
su eje mayorAE.
3
Construir
el óvaloconocido
los ejesTBytD.
l+
D
Consfruir
el óvaloconocido
su eje menortD.
€
5
[onstruirel ovoide
conocido
su eje menorfB.
6
o
@
z.
@
a
o
=
U
F
g
o
!¿
F
É
€¿
É
L
J
B
e
=
o
U
o
Construire[ ovoideconocido
su eje mayofT-8.
Construir
et ovoideconocidos
sus ejesTBy6.
Unidades
m :m . Nombre:
E s c ala
121
ó v a toy o v o i d e
Cu r so :
F e ch a :
N9
B-30| Nota:
Laespirales l¿ cu¡vadedescibeunpuntoquegiraalrededor
deotroatejándose
deé1.Pasoes la distancia
radialquehayentreespirasconsecutivas.
La espiralde Arquímedes
es el lugargeométrico
de [os puntosdel planocuyomódulo.distanciaal polo0, es proporcional
a su ángulopotar.
por arcosde circunferencia
Lavolutaes unacurvacompuesta
tangentesentresí. Losceni¡osde los arcosson los vérticesde un polígono.
2
Construirla espiralde dos centrossobreel segmenio
AB.
Construirta espiralde tres centrossobreel triángutoABC.
3
Construirun¿volutaa partir del círculo.
[ontinuarla construcción
de [a e:; piratdeArquímedes
o
ts
€
5
o
o
@
z
o
I
j
2
t0
F
o
3
óc
U
!¿
F
É
€¿
e
J
o
=
u
o
Construirla evolvente
de la cifcunferencia
a partir del puntoA.
Unidades:
m m . Nombre:
Escata
1:1
Espirales
Cu r so :
F e ch a :
Ng
B-31| Nota:
_
Ifl
t\"/t I
G
Mediopunto
0jivat
Escarzano
ffi
Deprimido
Carpanet
Herradura
2
T-rlT
tl
Trazarel arcode mediopunto.
Trazarel arcoojivalequilátero.
3
4
t---t
Trazarel afcoescarzano.
Trazarel arcodeorimido.
5
F
€
o
6
-t-- --T
] --I
I
@
-t
z
o
a
!¿
z
F
-t
Trazarel arcoconopial.
frazar el arcotrebolado.
71,
I
f
I
E
!¿
E
¿
ro
E
J
T--I--T
ril
J
I
o
=
o
U
quepasaporP.
Trazaret arcocarpanel
Trazarel arcode herradura.
o
U nidades
m :m .
Escata
1:1
Nombre:
--l
Arco sa r q u i te c tó n i c o s
fu r so :
F e ch a :
Ng
B-35| Nota:
v_ r
(-
t+
Corona
>r_
6orguera
Toro
t
+
h$-
t\
r---É
Bocel
Caveto
Gotarebajada
Escocia
2
Dibujarta gorguefa.
Dibujarla corona.
4
3
Dibujaret cuartobocel.
Dibujarel foro.
6
5
ts
N
o
z
2.
:
:¿
z
Dibujarel talón.
Dibujarel caveto,
7
I
q
z
a
a
U
Dibujarta golarebajada.
Unidades :
Escata
Dibujarta escocia.
Nombre:
Cu r so :
F e ch a :
Motdur aasr q u i te c tó n i c a s B-36
N9
Nota: