Solución láminas TANGENCIAS

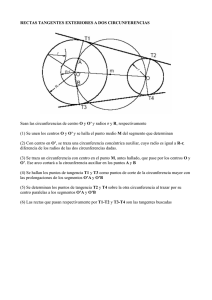
DIBUJO TÉCNICO
BACHILLERATO
Láminas resueltas del
TEMA 4. TANGENCIAS.
Departamento de Artes Plásticas
y Dibujo
1.- Dibujar 2 circunferencias radio 10 mm. que sean
TANGENTES EXTERIORES a la dada y entre ellas.
2.- Dibujar 2 circunferencias radio 10 mm. que sean
TANGENTES INTERIORES a la dada y entre ellas.
R = 10 mm
O2
O3
R = 10 mm
T1
R = 32 mm
T2
T1
O2
O1
R = 23 mm
O1
O3
T2
3.- Dibujar las circunferencias de r = 12 mm.,
TANGENTES a la dada y que pase por el PUNTO P.
4.- Circunferencias tangentes a otra de r = 18 mm. dada,
que pase por un punto P exterior y por un punto de
tangencia T.
P
O2
O1
T1
P
T
O1
T2
O3
R = 18 mm
El radio de la circunferencia que se busca se sabrá cuando se acabe
el ejercicio.
5.- Hallar las circunferencias tangentes
COMUNES EXTERIORES de r= 12 mm., a las
circunferencias dadas O1 y O2.
O1= 10 mm
O2 = 15 mm
6.- Hallar las circunferencias tangentes
COMUNES INTERIORES de r= 35 mm.,
a las circunferencias dadas O1 y O2. O1-O2 = 30
O1= 10 mm
O1-O2 = 40 mm
O2 = 15 mm
O3
O3
O2
O1
O4
Fecha
O4
Nombre alumno
N. lámina
Curso:
Nombre lámina
T 01
O2
O1
Nota:
TANGENCIAS ENTRE CIRCUNFERENCIAS
mm
1.-Dibuja la recta r tangente a la circunferencia O1
por el punto dado de tangencia (T).
2.- Dibuja la circunferencia de radio 13 mm. que
sea tangente a la recta dada y que pase por el
punto T dado.
O1
O1
T
T
3.- Dibuja las rectas tangentes a la circunferencia 01
dada y que pasen por P
4.- Dibuja la circunferencia de radio 15 mm. que
sea tangente a las rectas que se cortan dadas.
15 mm
O1
O1
P
15 mm
5.- Hallar las RECTAS tangentes COMUNES
EXTERIORES a las dos circunferencias dadas..
O1= 14 mm
O2 = 23 mm
6.- Hallar las RECTAS tangentes COMUNES
INTERIORES a las dos circunferencias dadas..
O1= 10 mm
O2 = 22 mm
T1
T1
T4
O2
T4
O1
O2
O1
T3
T3
T2
T2
Fecha
N. lámina
T 02
Nombre alumno
Curso:
Nombre lámina
Nota:
TANGENCIAS ENTRE RECTAS Y CIRCUNFERENCIAS
1.-Dibujar una circunferencia tangente a la recta r y que
pase por el punto P. (Circunferencia que pasa por 2
puntos)
2.- Circunferencias tangentes a una recta r dada, que
pasan por un punto P y que tiene de radio 20 mm.
P
o1
o1
o2
P
r
r
T
3.- Hallar las circunferencias tangentes a una recta r
y que pasan por dos puntos dados A y B. (aplicación de
eje radical)
4.- Dibujar las circunferencias tangentes a dos rectas
r y s dado el punto de tangencia T en una de ellas.
T2
o1
r
T
o1
T1
B
T
t
T
A
r
o2
o2
5.- Dibujar las circunferencias tangentes a O1 por el
punto de tangencia dado T y a la recta r.
6.- Representar las circunferencias de radio 20 mm.
tangentes comunes a la circunferencia y a la recta dadas.
Habrían dos resultados más al otro extremo de la
circunferencia O
o1
o
T
o2
o1
o2
o
r
r
Fecha
Nombre alumno
N. lámina
Curso:
Nombre lámina
T 03
Nota:
TANGENCIAS III
1.- Trazar tres circunferencias tangentes entre sí, dados
sus respectivos radios.
2.- Trazar tres circunferencias tangentes entre sí,
conocidos sus centros respectivos.
r1
r2
o2
o2
r3
T
T
r2
o1
r1
r3
T
T
o1
T
r3
T
o3
o3
3.- Dibujar las circunferencias de igual radio y tangentes
interiores a los lados de los ángulos de los vértices del
pentágono.
4.- Dibujar 4 circunferencias de igual radio y tangentes
interiores a la circunferencia dada.
o3
o
o´
o´
5.- Dadas las tres rectas r, s y t que se cortan entre sí,
trazar una circunferencia tangente común a las tres.
6.- Dibuja la circunferencia que es tangente a la recta r,
pasa por el punto P que está en la recta t y además
r
tiene el centro en t.
t
T
r
T
o
P
T
o
t
s
T
Fecha
Nombre alumno
N. lámina
Curso:
Nombre lámina
T 04
Nota:
TANGENCIAS IV
1.- Dibujar la circunferencia tangente a dos circunferencias O1 y O2, dado el punto de tangencia de una de ellas.
Método de eje radical.
1. Se dibuja una circunferencia auxiliar (O3) con centro en cualquier
punto de la recta t que une el punto de tangencia T con el centro
de la primera circunferencia O1. La circunferencia debe de pasar
por el punto T y cortar a la circunferencia de centro O2.
2. Se dibuja una recta tangente a O1 que pase por T
(perpendicular a t).(eje radical entre O1, O3 y las buscadas)
3. Por las intersecciones entre O3 y O2 (donde cortan)
se dibuja una recta que cortará a la recta tangente por T
en O4. (eje radical de O3 y O2.
4. Se dibuja una segunda circunferencia auxiliar de
centro O4 y radio O4T.
5. Esta circunferencia cortará a O2 en los puntos de
tangencia T´ y T´´.
6. Unimos O2 con T´ y con T´´ mediante dos rectas.
7. La prolongación de estas rectas cortará
respectivamente a t en O5 y en O6,
centros de las circunferencias buscadas.
O1
O5
T
O4
T´´
O6
O3
T´
t
O2
O3 punto cualquiera
2.- Dadas las rectas r y t y el punto P, dibujar las circunferencias tangentes a las rectas r y t y que pasen por P.
Aplicación de eje radical.
Solución: 1. dibujar la bisectriz del ángulo entre r y s. -2. Dibujar una recta perpendicular a la bisectriz y que pase
por el punto P. -3. Hallar el simétrico de P = Q. -4. Dibujar una circunferencia auxiliar que pase por P y por Q. En este
caso es la de centro O1, pero puede ser cualquiera. (La perpendicular que pasa por P y por Q será eje radical de las
circunferencias buscadas.)
5. Donde corta esta perpendicular
a la recta s será el punto R.
6. Desde R se halla la recta
tangente a O1 (será T1 y T2,
acordarse de rectas tangentes a
una circunferencia desde un punto
exterior).
7. Desde R se dibuja un arco de
radio Rt1 que cortará a s en los
puntos T3 y T4.
8. Desde estos puntos se levantan
perpendiculares a s hasta que
corten a la bisectriz en los centros
O2 y O3 respectivamente. Centros
de las circunferencias buscadas.
Han de pasar por T3, T4 y por P y Q.
r
P
O3
O1
O2
T1
T2
Q
T3
R
T4
s
Fecha
Nombre alumno
N. lámina
Curso:
Nombre lámina
T 05
Nota:
TANGENCIAS V
1.- Dibuja la circunferencia tangente exterior a O1 y a
la recta r por el punto de tangencia T.
1.- Dibuja la circunferencia tangente interior a O1 y a la
recta r por el punto de tangencia T.
O1
R
T
r
T
R
O1
R
T
r
R
T
1.- Dibuja las circunferencias tangentes a la circunferencia dada O y que pase por los puntos M y N
Fecha
Nombre alumno
N. lámina
Curso:
Nombre lámina
T 06
Nota:
TANGENCIAS VI
1.- Determine todas las circunferencias tangentes a la circunferencia C y a la recta r en el punto T.
- Indique los centros de los arcos a trazar y los puntos de tangencia. No borre las operaciones auxiliares que permiten determinarlos.
Solución por medio de POTENCIA. EJE RADICAL.
C
r
O1
O
T
O2
Fecha
Nombre alumno
N. lámina
Curso:
Nombre lámina
T 07
Nota:
TANGENCIAS ejercicio PAU Junio 2012
1.- Determine todas las circunferencias tangentes a la circunferencia C y a la recta r en el punto T.
- Indique los centros de los arcos a trazar y los puntos de tangencia. No borre las operaciones auxiliares que permiten determinarlos.
Solución por medio de TANGENCIAS. El radio de la circunferencia se pone a un lado y a otro de la recta r por T.
T2
C
r
O
T
T1
Fecha
Nombre alumno
N. lámina
Curso:
Nombre lámina
T 07
Nota:
TANGENCIAS ejercicio PAU Junio 2012
2.-Dado el croquis de la figura, obtenga el dibujo a
Escala 1:2, indicando los centros de los arcos a trazar
y los puntos de tangencia entre los diversos arcos y
rectas.
100
O3
O1 y O2 por posición de datos según acotación.
O3 según arcos con centro O1 y O2 respectivamente y radio:
O1+O3 y O2+O3
T
O1
T
r
T
O2
T
O5
O4
T
Dibujar un ángulo de 30º desde la paralela a la base de 30 mm
(escala 1:2) y como centro del vértice O2, se halla así el
punto de tangencia. Por él trazar una perpendicular a la prolongación
O2-T por T y que corte a la línea base. En ese punto se dibuja
una curva hasta T y que corte a la línea base o bien se halla
la bisectriz de los ángulos que forma. Hallamos entonces O4.
(Caso de circunferencia tangente entre una circunferencia y
una recta cuando el punto de tangencia está en la circunferencia dada)
r
Se coloca el radio de O1 bajo
la línea base y a partir de T.
Se une con O1 y se halla la
bisectriz. Donde corte ésta
con la perpendicular por T
estará O5.
(Caso de circunferencia
tangente a una circunferencia
y a una recta cuando el punto
T está en la recta)
Fecha
Nombre alumno
Curso:
N. lámina
Nombre lámina
Nota: