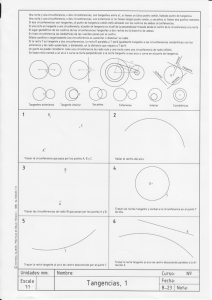
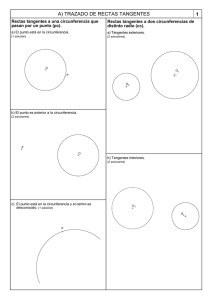
rectas tangentes a circunferencias

UNIDAD 9 Problemas métricos en el plano
7. Ampliación teórica:
rectas tangentes a circunferencias
Pág. 1 de 2
Estas son las posiciones relativas de una recta y una circunferencia:
O
O
O
d<r
d=r
d>r
SECANTES
TANGENTES
EXTERIORES
Se cortan en dos puntos.
Se cortan en un punto.
No tienen ningún punto común.
Tangente desde un punto a una circunferencia
Desde un punto exterior se pueden trazar dos tangentes a una circunferencia. Cada una de ellas es perpendicular al radio en el punto de tangencia. Por tanto, el triángulo de lados d, r y t es rectángulo:
d 2 = r2 + t2
T
t
r
P
d
O
Veamos un ejemplo.
Si se traza una circunferencia de 15 cm de radio con centro en un punto O, y desde un punto P que dista
39 cm de O se traza una recta tangente en T a la circunferencia, podemos hallar la longitud PT del siguiente modo:
T
15 cm
P
39 cm
O
PT = √392 – 152 = 36 8 PT = 36 cm
UNIDAD 9 Problemas métricos en el plano
7. Ampliación teórica:
rectas tangentes a circunferencias
Pág. 2 de 2
Tangentes comunes a dos circunferencias
T
T
t
T'
r
t
r'
O
O
O'
d
T'
r
r'
O'
d
t'
t'
Tanto si las circunferencias son exteriores como si son secantes, se pueden trazar dos rectas tangentes comunes
exteriores a las dos circunferencias. El cuadrilátero TT'O'O es un trapecio rectángulo.
Si las circunferencias son externas, tienen, además, dos tangentes comunes interiores.
r
r'
O'
O
Las correas sinfín son una aplicación de las tangentes comunes a dos circunferencias.
Cuando las ruedas han de girar en el mismo sentido, las correas serán tangentes
exteriormente.
Si las ruedas han de girar en sentido inverso, las correas serán tangentes interiormente.
t1
r
Veamos un ejemplo.
t2
O
r'
O'
d = 20 cm
t2
O
t2
d = 20 cm
OO' = 20 cm,
El triángulo sombreado en verde es rectángulo. La hipotenusa es d = 20 cm.
Los catetos son r + r' = 14 cm y t2, longitud del segmento buscado.
r'
r
En estas circunferencias, r = 9 cm, r' = 5 cm y
t1 = 19,6 cm. Calculemos t2 (tangente interior).
O'
r'
t2 = √202 – 142 = 14,3 cm