a) trazado de rectas tangentes 1

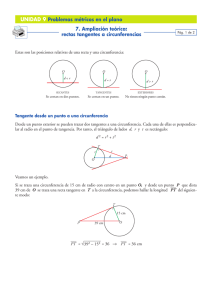
A) TRAZADO DE RECTAS TANGENTES
1
Rectas tangentes a una circunferencia que
pasan por un punto (pc).
Rectas tangentes a dos circunferencias de
distinto radio (cc).
a) El punto está en la circunferencia.
a) Tangentes exteriores.
(1 solución)
(2 soluciones)
O
O1
P
O2
b) El punto es exterior a la circunferencia.
(2 soluciones)
P
O
b) Tangentes interiores.
(2 soluciones)
c) El punto está en la circunferencia y el centro es
desconocido. (1 solución)
O1
O2
P
B) TRAZADO DE CIRCUNFERENCIAS TANGENTES CONOCIENDO EL RADIO 2
Circunferencias que pasan por un punto y son tangentes a una recta (Rpr).
a) El punto está en la recta.
b) El punto es exterior.
(2 soluciones)
(2 soluciones)
R
R
r
M
M
r
Circunferencias que pasan por un punto y son tangentes a una circunferencia (Rpc).
a) El punto está en la circunferencia.
b) El punto es exterior.
(2 soluciones)
(4 soluciones máximo)
R
R
M
O
M
O
Circunferencias tangentes a dos rectas que se cortan (Rrr).
(4 soluciones)
R
s
r
B) TRAZADO DE CIRCUNFERENCIAS TANGENTES CONOCIENDO EL RADIO 3
Circunferencias tangentes a una recta y a una circunferencia (Rrc).
a) La circunferncia y la recta son exteriores.
b) La circunferencia y la recta son tangentes.
(4 soluciones máximo)
(4 soluciones)
R
R
O
O
r
r
c) La circunferencia y la recta son secantes.
(8 soluciones máximo)
Circunferencias tangentes a dos circunferencias (Rcc).
a) Las circunferencias son exteriores.
(8 soluciones máximo)
R
O’
b) Las circunferencias son tangentes.
(4 soluciones)
c) Las circunferencias son secantes.
(8 soluciones máximo)
O’’
ENLACES
Enlazar dos rectas que se cortan mediante un arco de
radio conocido.
4
Enlazar dos rectas que se cortan mediante un arco,
conociendo el punto de tangencia en una de ellas.
R
s
s
T
r
Enlazar dos rectas paralelas mediante dos arcos de
igual radio, conociendo los dos puntos de tangencia.
Enlazar dos rectas cualesquiera mediante dos arcos,
conociendo el radio de uno de ellos y los puntos de
tangencia.
s
R
M
r
s
N
N
r
Enlazar una recta y un arco mediante otro arco de
radio conocido.
R
M
r
Enlazar una recta y un arco mediante otro arco,
conociendo el punto de tangencia con la circunferencia.
O
O
T
r
r
Enlazar una recta y un arco mediante otro arco,
conociendo el punto de tangencia con la recta.
Enlazar dos arcos de circunferencia mediante otro
arco de radio conocido.
R
O
O’
T
r
O’’
C) TRAZADO DE CIRCUNFERENCIAS TANGENTES SIN CONOCER EL RADIO
5
Circunferencias que pasan por dos puntos y son tangentes a una recta (ppr).
b) Un punto está en la recta.
(2 soluciones)
(1 solución)
APLICACIÓN DE POTENCIA
a) Los puntos son exteriores.
M
M
N
r
N
r
Circunferencias que pasan por un punto y son tangentes a dos rectas (prr).
a) El punto es exterior.
b) El punto está en una de las rectas
(2 soluciones)
(2 soluciones)
s
APLICACIÓN DE POTENCIA
s
M
M
r
r
Circunferencias que pasan por dos puntos y son tangentes a una circunferencia (ppc).
a) Los puntos son exteriores.
b) Un punto está en la circunferencia
(2 soluciones)
(1 solución)
APLICACIÓN DE POTENCIA
M
O
N
M
O
N
C) TRAZADO DE CIRCUNFERENCIAS TANGENTES SIN CONOCER EL RADIO
Circunferencias tangentes a tres rectas que se cortan (rrr).
(4 soluciones)
t
s
r
Circunferencias que pasan por un punto y son tangentes a una recta y a una circunferencia (prc).
a) El punto es exterior
APLICACIÓN DE INVERSIÓN Y POTENCIA
(4 soluciones)
O
M
r
b) El punto está en la recta
APLICACIÓN DE INVERSIÓN
(2 soluciones)
O
r
M
6
C) TRAZADO DE CIRCUNFERENCIAS TANGENTES SIN CONOCER EL RADIO
Circunferencias que pasan por un punto y son tangentes a dos circunferencias (pcc).
a) El punto es exterior.
(4 soluciones: 2 soluciones se obtienen con el centro
de inversión intersección de las rectas tangentes
exteriores a las circunferencias dadas)
APLICACIÓN DE INVERSIÓN Y POTENCIA
M
O1
O2
a) El punto es exterior.
APLICACIÓN DE INVERSIÓN Y POTENCIA
(4 soluciones: 2 soluciones se obtienen con el
centro de inversión intersección de las rectas
tangentes interiores a las circunferencias dadas)
M
O1
O2
b) El punto está en una circunferencia.
(2 soluciones)
O’
APLICACIÓN DE POTENCIA
M
O
7
C) TRAZADO DE CIRCUNFERENCIAS TANGENTES SIN CONOCER EL RADIO
Circunferencias tangentes a tres circunferencias: problema de Apolonio (ccc).
(8 soluciones)
Obtener sólo 2 soluciones: una tangente exterior a las tres circunferencias dadas y
otra tangente interior a las tres dadas.
Procedimiento: Dilatación negativa para reducir el ejercicio a circunferencias tangentes
que pasan por un punto y son tangentes a otras dos (caso ya estudiado). Aplicaremos
también el concepto de inversión y potencia.
Centro de inversión positivo
P2 - P1
P3 - P1
P1
P2
P3
8a
C) TRAZADO DE CIRCUNFERENCIAS TANGENTES SIN CONOCER EL RADIO
Circunferencias tangentes a tres circunferencias: problema de Apolonio (ccc).
(8 soluciones)
Otras 2 soluciones:
- Una circunferencia solución será tangente exterior a las dos circunferencias dadas
y tangente interior a la otra.
- Y la otra solución será tangente interior a dos y exterior a la otra.
Procedimiento: Dilatación positiva para reducir el ejercicio a circunferencias tangentes
que pasan por un punto y son tangentes a otras dos (caso ya estudiado). Aplicaremos
también el concepto de inversión (positiva) y posteriormente el de potencia.
P1
P2
P3
Centro de inversión positivo
P2 + P1
P3 + P1
8b
C) TRAZADO DE CIRCUNFERENCIAS TANGENTES SIN CONOCER EL RADIO
Circunferencias tangentes a tres circunferencias: problema de Apolonio (ccc).
(8 soluciones)
Otras 2 soluciones:
- Una circunferencia solución será tangente exterior a las dos circunferencias dadas y tangente
interior a la otra.
- Y la otra solución será tangente interior a dos y exterior a la otra.
Procedimiento: Dilatación positiva en P2 y dilación negativa en P3 para reducir el ejercicio a
circunferencias tangentes que pasan por un punto (P1) y son tangentes a otras dos (caso ya
estudiado). Aplicaremos también el concepto de inversión (negativa) y posteriormente el de
P1
P2
P3
Centro de inversión negativo
P2 + P1
P3 - P1
8c
C) TRAZADO DE CIRCUNFERENCIAS TANGENTES SIN CONOCER EL RADIO
Circunferencias tangentes a tres circunferencias: problema de Apolonio (ccc).
(8 soluciones)
Otras 2 soluciones:
- Una circunferencia solución será tangente interior a las dos circunferencias dadas y tangente exterior
a la otra.
- Y la otra solución será tangente exterior a dos e interior a la otra.
Procedimiento: Dilatación positiva en P3 y dilación negativa en P2 para reducir el ejercicio a
circunferencias tangentes que pasan por un punto ( P1) y son tangentes a otras dos (caso ya
estudiado). Aplicaremos también el concepto de inversión (negativa) y posteriormente el de potencia.
P1
P2
P3
Centro de inversión negativo
P2 - P1
P3 + P1
8d
POTENCIA: EJE RADICAL Y CENTRO RADICAL
EJE RADICAL DE DOS CIRCUNFERENCIAS SECANTES
O1
0
EJE RADICAL DE DOS CIRCUNFERENCIAS TANGENTES
(EXTERIORES)
O2
O2
O1
EJE RADICAL DE DOS CIRCUNFERENCIAS TANGENTES
(INTERIORES)
EJE RADICAL DE DOS CIRCUNFERENCIAS EXTERIORES
O2
O2
O1
O1
EJE RADICAL DE DOS CIRCUNFERENCIAS INTERIORES
CENTRO RADICAL DE TRES CIRCUNFERENCIAS
O1
O1
O2
O2
O3
TANGENTES DESDE EL EJE RADICAL
TANGENTES DESDE EL CENTRO RADICAL
O’’
O3
O1
O’
O2