MaquetaciÛn 1
Anuncio

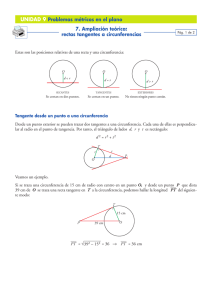
4 UNIDAD Generalización del estudio de tangencias CONOCIMIENTOS TEÓRICOS 1 Potencia respecto a una circunferencia 1.1 Concepto de potencia. Expresiones de la misma 1.2 Eje radical de dos circunferencias. Propiedades 1.3 Centro radical de tres circunferencias. Propiedades 2 Propiedades de las tangentes a las cónicas 2.1 Elipse 2.2 Parábola 2.3 Hipérbola APLICACIONES PRÁCTICAS 1 Tangencias con circunferencias 1.1 Casos posibles 1.2 Resoluciones basadas en el eje radical 1.3 Resoluciones basadas en la inversión 2 Tangencias con otras cónicas 2.1 Tangentes a la elipse 2.2 Tangentes a la parábola 2.3 Tangentes a la hipérbola CUESTIONES Y EJERCICIOS UNIDAD 4 CONOCIMIENTOS TEÓRICOS Generalización del estudio de tangencias En la unidad 5 de Dibujo técnico 1 estudiamos los casos más habituales de tangencias, estudio que completaremos en la presente unidad con la sistematización de los mismos, ampliando al mismo tiempo los procedimientos de resolución. Este tema se completa con el trazado de tangencias a las restantes curvas cónicas. 1 POTENCIA RESPECTO A UNA CIRCUNFERENCIA Un punto y una circunferencia situados en el mismo plano pueden relacionarse a través del concepto de potencia, a partir del cual definiremos los denominados elementos radicales, eje y centro radical. Lo vemos a continuación: 1.1 Concepto de potencia. Expresiones de la misma La potencia de un punto P respecto de una circunferencia puede definirse como el producto de las distancias entre el punto y los puntos de corte de una cualquiera de las secantes trazada desde P. Para cualquiera de las dos circunferencias de la figura 1 ha de cumplirse: Pot = PA · PB Fig. 1 Cuando el punto es exterior a la circunferencia, la potencia es positiva, y en el caso de puntos interiores, negativa. Los puntos pertenecientes a la circunferencia tienen potencia cero respecto a esa circunferencia. Fig. 2 76 La expresión y el valor de la potencia son independientes de la secante que utilicemos; así, en la figura 2, trazamos dos secantes distintas desde un mismo punto P. Los triángulos PBC y PDA son semejantes al tener iguales Generalización del estudio de tangencias TEÓRICOS UNIDAD CONOCIMIENTOS UNIDAD CONOCIMIENTOS TEÓRICOS sus tres ángulos: el ángulo de vértice en P es común a ambos triángulos y los ángulos de vértices en B y D son iguales, por estar inscritos en la misma circunferencia y abarcar el mismo arco; por tanto, podremos establecer, entre los dos triángulos, la siguiente proporcionalidad: PA PD = PC PB Esta proporción demuestra que los productos PA · PB y PC · PD son iguales e independientes de la secante utilizada. A la igualdad entre estos dos productos, también habríamos llegado al considerar los segmentos AD y BC como antiparalelos de PB y PD, por ser iguales los ángulos de vértices en B y D, siendo, por tanto, iguales los productos entre PA · PB y entre PC · PD. En la figura 3, podemos considerar la tangente a la circunferencia trazada desde el punto P como la posición límite de una secante; el punto de tangencia T es un punto doble. Del análisis de esta figura, deducimos dos expresiones de la potencia: Fig. 3 • La tangente trazada desde el punto P a la circunferencia, segmento PT, es la expresión gráfica de la potencia de ese punto respecto a dicha circunferencia, segmento del que nos serviremos al utilizar la potencia en la resolución de tangencias. • Aplicamos el teorema de Pitágoras al triángulo PTO; la hipotenusa es la expresión gráfica de la potencia, segmento PT, siendo los catetos el radio de la circunferencia y la distancia al centro desde el punto P. Pot = d2 – r2 1.2 Eje radical de dos circunferencias. Propiedades El eje radical de dos circunferencias lo constituyen los puntos del plano que tienen la misma potencia respecto a dichas circunferencias. Los puntos del eje radical definen un lugar geométrico. Para determinar gráficamente la posición del eje radical, consideraremos las dos circunferencias secantes de la figura 4; sus puntos de intersección, A y B, tienen potencia cero respecto a cada una de ellas; dichos puntos, por tener igual potencia, pertenecen al eje radical de ambas circunferencias, definiendo su posición en el plano. Fig. 4 En la figura anterior observamos, también, que la recta que une los centros O1 y O2 de las dos circunferencias es la mediatriz del segmento AB; es decir, el eje radical es perpendicular a la recta que une los centros de las dos circunferencias. 77 4 UNIDAD 4 CONOCIMIENTOS TEÓRICOS Generalización del estudio de tangencias Utilizando la propiedad anterior, nos basta un único punto para trazar el eje radical de dos circunferencias. En las circunferencias tangentes de la figura 5, su punto de tangencia T, por tener potencia cero respecto a ambas, define el punto de paso de su eje radical, que trazaremos perpendicularmente a O1-O2. Fig. 5 En el caso de dos circunferencias exteriores o interiores (Fig. 6 y 7), determinaremos el eje radical con ayuda de una tercera circunferencia auxiliar, secante a ambas; entre ésta y las de centros O1 y O2 podemos establecer sendos ejes radicales, e1 y e1, cuya intersección nos marcará el punto de paso P del eje radical buscado, que trazaremos perpendicularmente a O1O2. También podríamos buscar un segundo punto perteneciente al eje radical con ayuda de una nueva circunferencia auxiliar. Fig. 6 Fig. 7 Si desde un punto cualquiera P del eje radical de dos circunferencias trazamos las tangentes a las mismas (Fig. 8), los segmentos tangentes t1 y t2 tendrán la misma longitud, ya que todos los puntos del eje radical tienen la misma potencia. Esta propiedad será de utilidad en la resolución de algunos problemas de tangencias. Si trazamos una de las circunferencias con centro en el eje radical y que sea secante a las de centro O1 y O2, los radios O1T1 y PT1 son perpendiculares, por lo que diremos que dichas circunferencias son ortogonales. El eje radical de dos circunferencias será, también, lugar geométrico de los centros de las circunferencias ortogonales a dichas circunferencias. Fig. 8 1.3 Centro radical de tres circunferencias. Propiedades El centro radical CR de tres circunferencias es el punto que tiene igual potencia respecto a las tres. Se halla en la intersección de los ejes radicales de las circunferencias, tomadas éstas dos a dos. Así, en la figura 9, el centro radical se ha determinado como intersección de los ejes radicales e1 y e2; el tercer eje radical, no dibujado, también pasaría por CR. 78 Generalización del estudio de tangencias CONOCIMIENTOS TEÓRICOS UNIDAD Si desde el centro radical trazamos las tangentes a las tres circunferencias (Fig. 10), los seis segmentos comprendidos entre CR y cada una de las circunferencias tendrán la misma longitud. Esta longitud es el radio de una circunferencia de centro CR, la cual es ortogonal a las otras tres. Fig. 9 Fig. 10 2 PROPIEDADES DE LAS TANGENTES A LAS CÓNICAS En la unidad 1 del presente libro estudiamos las curvas cónicas; en ésta, partiendo de sus características y conociendo la construcción de cada una de ellas, veremos las propiedades que permiten el trazado de rectas tangentes a las mismas. 2.1 Elipse Los ejes AB y CD de la figura 11 definen una elipse con centro en su punto O de intersección. Con centro en C o D y con un radio igual a la longitud del semieje OA, determinamos los focos F y F’ de la elipse. La circunferencia principal Cp tiene por centro el punto O de la elipse y su radio es la longitud OA. Esta circunferencia es el lugar geométrico de los pies de las perpendiculares trazadas desde los focos a cada una de las tangentes a la cónica; es decir, que si desde Fig. 11 79 4 UNIDAD 4 CONOCIMIENTOS TEÓRICOS Generalización del estudio de tangencias uno de los focos, F’ en la figura 11, trazamos la perpendicular a una tangente t1 de la elipse, el pie de la perpendicular P es un punto de la circunferencia principal Cp. Las circunferencias focales Cf y Cf’ tienen por centro, respectivamente, cada uno de los focos de la elipse y un radio igual a la longitud de su eje real AB. El centro M de cualquier circunferencia que, pasando por uno de los focos, sea tangente a la circunferencia focal del otro foco está situado sobre la elipse. Esta propiedad hace que la elipse puede también definirse como el lugar geométrico de los centros de las circunferencias que pasan por uno de los focos y son tangentes a la circunferencia focal del otro. Del análisis de la figura 11, y a partir de las propiedades que acabamos de definir, podemos establecer las siguientes reglas, que han de permitirnos trazar rectas tangentes a una elipse cualquiera: • La tangente a una elipse, trazada por un punto M cualquiera de ella, es la bisectriz del ángulo formado por el radio vector MF y la prolongación del otro MF’. • Respecto a una recta tangente a la elipse, el punto simétrico de uno de los focos se halla sobre la circunferencia focal del otro foco. T es el simétrico de F respecto a la tangente t2, siendo ésta, lógicamente, la mediatriz del segmento FT. 2.2 Parábola Si conocemos la posición del vértice V y del foco F de una parábola, ya podemos efectuar su trazado. La recta que pasa por ambos puntos define el eje de simetría de la parábola. El vértice V es el punto medio entre el foco y la directriz, siendo ésta última perpendicular al eje (Fig. 12). Fig. 12 Al tratarse de una curva abierta, su circunferencia principal Cp es de radio infinito, coincidiendo su posición con la directriz de la parábola. Como en la elipse, la circunferencia principal (directriz en la parábola) es el lugar geométrico de los puntos simétricos del foco respecto de cada tangente. El centro M de cualquier circunferencia que, pasando por el foco, sea tangente a la directriz está situado sobre la parábola. Esta propiedad hace que la parábola puede también definirse como el lugar geométrico de los centros de las circunferencias que pasan por el foco y son tangentes a la directriz. La tangente a la parábola trazada por su vértice es una recta paralela a la directriz y coincide con la circunferencia focal, Cf, que, como la Cp, es de radio infinito. Esta recta es el lugar geométrico de los pies de las perpendiculares trazadas desde el foco a cada una de las tangentes a la cónica; es decir, que si desde el foco trazamos la perpendicular a una tangente t de la parábola, el pie de la perpendicular es un punto de la tangente a la parábola trazada por el vértice. 80 Generalización del estudio de tangencias CONOCIMIENTOS TEÓRICOS UNIDAD A partir de las propiedades que acabamos de definir y del análisis de la figura 12, podemos establecer algunas reglas que han de permitirnos trazar rectas tangentes a la parábola: • La tangente t en un punto M de la parábola es la bisectriz de los radios vectores MT y MF. • El punto simétrico del foco respecto a una tangente a la parábola está situado en la directriz. 2.3 Hipérbola Como en la elipse, la hipérbola tiene seis puntos característicos: los focos F y F’ y los cuatro vértices A, B, C y D. Conocidos cuatro de estos puntos, podemos determinar los dos restantes y trazar la curva o determinar sus tangentes. En la figura 13 conocemos los extremos del eje real, vértices A y B, y la posición de los focos, F y F’; los extremos C y D del eje imaginario se hallan sobre la mediatriz del segmento AB y a una distancia de A o B igual a la longitud del segmento OF. La hipérbola también la podemos definir como el lugar geométrico de puntos que son centros de las circunferencias que, pasando por uno de los focos, son tangentes a la circunferencia focal del otro foco; en ella podremos trazar las dos circunferencias a las que nos hemos referido en las cónicas anteriores, la principal Cp, con centro en O y con radio igual a la mitad de la distancia entre A y B, y las focales Cf, con centro en los focos y con radio igual al segmento AB. Fig. 13 Las circunferencias anteriores tienen las propiedades ya enunciadas al hablar de elipse y parábola, por lo que podremos establecer las siguientes reglas que nos permitirán el trazado de las tangentes a la cónica: • La tangente a una hipérbola trazada desde un punto M cualquiera de ella es la bisectriz del ángulo formado por los radios vectores MF y MF’, los cuales unen ese punto con los focos. • Respecto a una recta tangente a la hipérbola, el punto simétrico de uno de los focos se halla sobre la circunferencia focal del otro foco. T es el simétrico de F respecto a la tangente t, siendo ésta, lógicamente, la mediatriz del segmento FT. Oscar Niemeyer. Catedral metropolitana, Brasilia. 81 4 UNIDAD 4 APLICACIONES PRÁCTICAS Generalización del estudio de tangencias 1 TANGENCIAS CON CIRCUNFERENCIAS El trazado de rectas tangentes ya es conocido desde Dibujo técnico 1. Veremos ahora las tangencias en que las soluciones a determinar son circunferencias; el procedimiento utilizado deriva de la aplicación de elementos radicales o del concepto de inversión. 1.1 Casos posibles Consideremos los siguientes elementos intervinientes en un problema de tangencias: punto, P, recta, R, y circunferencia, C. Estos elementos, agrupados de tres en tres, y con la posibilidad de que alguno de ellos aparezca repetido, dan lugar a las diez combinaciones siguientes: PPP, PPR, PPC, PRR, PRC, PCC, RRR, RRC, RCC, CCC Para cualquiera de estas combinaciones, debemos determinar la circunferencia o circunferencias que, pasando por el punto o puntos dados (en los casos en que los haya), sean tangentes a los restantes elementos de la combinación; así, PCC, por ejemplo, significa buscar las circunferencias que, pasando por un punto P, sean tangentes a dos circunferencias también dadas. Las combinaciones PPP y RRR tienen una resolución ya conocida y en la que no nos detendremos. La primera de ellas, circunferencia que pasa por tres puntos, tiene su centro en el punto de intersección de las mediatrices de los segmentos formados por los tres puntos, tomados dos a dos; lógicamente, estos puntos no pueden estar alineados. Para encontrar el centro de las circunferencias tangentes a tres rectas, RRR, deberemos buscar las bisectrices de los ángulos que forman. Para resolver los restantes casos, los agrupamos en dos bloques, el primero, PPR, PPC, PRR y CRR, lo resolvemos a continuación como aplicación de elementos radicales. Los cuatro restantes, PCR, PCC, CCR y CCC, los resolveremos en el apartado 1.3 aplicando el concepto de inversión. 1.2 Resoluciones basadas en el eje radical Cuando resolvemos un problema de tangencias, aplicando elementos radicales, seguimos el siguiente proceso: buscamos el centro radical CR, punto con la misma potencia respecto a las circunferencias solución y a las del enunciado, caso de existir éstas. El CR se halla, lógicamente, en la intersección de dos ejes radicales; para el trazado de alguno de éstos, es necesario, a veces, dibujar una circunferencia auxiliar que guarde relación con los datos del enunciado. Lo vemos más claramente resolviendo los siguientes cuatro casos: PPR, PPC, PRR y CRR. 82 Generalización del estudio de tangencias APLICACIONES PRÁCTICAS UNIDAD • Circunferencias tangentes a una recta pasando por dos puntos dados, PPR Dadas una recta r y dos puntos, P y Q, se trata de encontrar las circunferencias tangentes a la recta que pasen por los dos puntos dados. Por dos puntos, P y Q, pasan infinitas circunferencias, entre las que se incluyen las que sean tangentes a la recta r; todas ellas tendrán al segmento PQ como eje radical común, ER1 en la figura 14. La recta r, tangente a las dos circunferencias solución, es también eje radical ER2 de todos los haces de circunferencias tangentes en cada uno de sus puntos. La intersección del segmento PQ con la recta r, intersección de dos ejes radicales, define la posición del centro radical CR entre las circunferencias buscadas y cualquier otra que pase por P y Q. Fig. 14 Todas las circunferencias que pasen por P y Q tendrán su centro en la mediatriz del segmento que definen, mediatriz que en la figura denominamos recta de centros. Trazamos una circunferencia auxiliar de centro en el punto medio de PQ y cuyo diámetro es la longitud de dicho segmento; esta circunferencia satisface dos de las tres condiciones que han de cumplir las circunferencias solución (tener el centro en la mediatriz de PQ, pasar por P y Q y ser tangente a r). La potencia del CR respecto a la circunferencia auxiliar es la misma que la que tendrá CR en relación a las circunferencias solución. 83 4 UNIDAD 4 APLICACIONES PRÁCTICAS Generalización del estudio de tangencias Desde CR trazamos la tangente a la circunferencia auxiliar, segmento que representa, gráficamente, el valor de la potencia. Con centro en CR y con radio igual a la magnitud de la potencia, trazamos un arco que corta a la recta r en los puntos de tangencia T1 y T2; desde ellos levantamos perpendiculares a r hasta interceptar, sobre la recta de centros, los puntos O1 y O2, centros de las circunferencias solución. Con los mismos elementos, PPR, en las figuras 15 y 16 resolvemos dos casos singulares; en el primero de ellos, el punto P es el de tangencia sobre la recta r, y en el segundo, ambos puntos definen un segmento paralelo a r. Del análisis gráfico de las figuras puede deducirse, fácilmente, el proceso de resolución seguido. Fig. 15 • Circunferencias tangentes a una circunferencia pasando por dos puntos dados, PPC Dada una circunferencia de centro O y dos puntos A y B, queremos trazar las circunferencias que, pasando por dichos puntos, sean tangentes a la circunferencia. La mediatriz del segmento AB es la recta de centros sobre la que se encontrarán los de las circunferencias solución (Fig. 17). Seguimos el proceso de resolución referido al inicio del apartado: • Trazamos una circunferencia auxiliar, con el centro sobre la recta de centros, que pase por los puntos dados A y B y que corte a la circunferencia inicial de centro O. Fig. 16 Fig. 17 84 Generalización del estudio de tangencias APLICACIONES PRÁCTICAS UNIDAD • La recta que definen A y B es el eje radical ER1 entre las circunferencias solución. El segundo eje radical, ER2, pasa por los puntos de intersección de la circunferencia auxiliar con la de centro O. • La intersección de los dos ejes radicales es el centro radical CR. Desde él trazamos la tangente a la circunferencia auxiliar, tangente cuya longitud coincide con el valor de la potencia. • Con centro en CR y con radio igual a la longitud del segmento representativo de la potencia, trazamos un arco que intercepta, sobre la circunferencia de centro O, los puntos de tangencia T1 y T2. • Las rectas que unen T1 y T2 con O, al cortar a la recta de centros, fijan la posición de los centros de las circunferencias solución. Con los mismos elementos, PPC, consideramos otros casos de fácil resolución, al ocupar los puntos A y B posiciones particulares en relación a la circunferencia y a su centro O (Fig.18, 19 y 20). Fig. 18 Fig. 19 Fig. 20 • Circunferencias tangentes a dos rectas pasando por un punto dado, PRR Para que las circunferencias solución sean tangentes a r y s, la recta de centros será la bisectriz del ángulo que forman (Fig. 21). Desde P trazamos la perpendicular a la bisectriz y buscamos su simétrico P’ respecto a ella. Las circunferencias solicitadas pasarán por los puntos P y P’, siendo tangentes a la recta r; es decir, que hemos transformado el problema planteado en otro, PPR, resuelto en el primer subapartado de 1.2. Fig. 21 85 4 UNIDAD 4 APLICACIONES PRÁCTICAS Generalización del estudio de tangencias La recta r define la posición del primer eje radical, ER1, y PP’, la del segundo, ER2; la intersección de ambos es el centro radical CR, desde el cual trazamos la tangente a la circunferencia auxiliar de diámetro PP’. Con centro en CR y con un radio igual a la longitud de la tangente a la circunferencia auxiliar (valor de la potencia), trazamos un arco que corta a r en los puntos de tangencia T1 y T2; desde ellos levantamos perpendiculares a r, las cuales cortan a la bisectriz en los centros de las circunferencias solución. Antes de proceder a su trazado, buscaremos los puntos de tangencia en la segunda de las rectas, la s. Como en casos anteriores, indicamos, para los mismos elementos, otras posiciones en las que la resolución puede leerse gráficamente a partir de las representaciones efectuadas: en la figura 22 el punto P está situado sobre la recta s, mientras que en la figura 23 las rectas r y s son paralelas, siendo P un punto interior a ambas. Fig. 22 Fig. 23 • Circunferencias tangentes a dos rectas y a una circunferencia comprendida entre ellas, CRR Partimos de dos rectas r y s y de una circunferencia, de centro O y radio R, comprendida entre ellas; encontraremos las circunferencias solución, tangentes a las rectas y a la circunferencia inicial, transformando el problema en otro: dibujar las tangentes a dos rectas pasando por un punto. Para efectuar esta transformación, se resta el radio R a todos los elementos del sistema: la circunferencia queda reducida a un punto, su centro O, y las dos rectas r y s se convierten en otras dos paralelas, r’ y s’, a una distancia R. El problema se transforma en dibujar las circunferencias tangentes a las rectas transformadas r’ y s’ y que pasen por el punto centro O de la circunferencia, caso que hemos denominado PRR y que hemos resuelto en el apartado anterior. 86 Generalización del estudio de tangencias APLICACIONES PRÁCTICAS UNIDAD En la figura 24 hemos trazado las paralelas r’ y s’ hacia el exterior del ángulo formado por r y s; en relación a ellas y con el punto O, realizamos el proceso de resolución del caso PRR. Con centro en CR y con un radio igual al valor de la potencia, trazamos un arco que determina sobre r’ los puntos de tangencia A y B; a partir de ellos, sumamos el radio R de la circunferencia inicial para obtener los puntos de tangencia T1 y T2 sobre la recta r; desde éstos determinamos los centros O1 y O2, y los puntos de tangencia sobre la segunda de las rectas. Todo ello se hará previamente al trazado de las circunferencias solución. Pero el problema planteado tiene otras dos soluciones; las obtenemos en la figura 25 realizando la operación de restar el radio R a las dos rectas, ahora hacia el interior del ángulo. Cuando tenemos la posición del centro radical CR, llevamos la magnitud de la potencia sobre r’ para determinar los puntos A y B, desde los cuales, sumando el radio R, encontramos T1 y T2 sobre la recta r. A partir de estos puntos, completamos el trazado tal como hemos hecho con las otras dos soluciones. Fig. 24 1.3 Resoluciones basadas en la inversión El concepto de inversión lo estudiamos en la unidad 3 y lo aplicamos a la resolución de tangencias, en concreto, al caso de circunferencias tangentes a una recta y a una circunferencia, pasando por un punto; a este caso lo denominamos PCR. Para completar el estudio de las diez combinaciones indicadas anteriormente y que podemos formar con un punto P, una circunferencia C y una recta R, nos faltan tres casos, PCC, CCR y CCC, que veremos a continuación. Fig. 25 87 4 UNIDAD 4 APLICACIONES PRÁCTICAS Generalización del estudio de tangencias • Circunferencias tangentes a otras dos pasando por un punto, PCC En la resolución de este caso (Fig. 26) y en los próximos, resueltos todos ellos como aplicación del concepto de inversión, describiremos únicamente el proceso de realización, pero sin entrar en las construcciones particulares que nos permiten transformar una figura en su inversa, o deshacer la inversión mediante la cual hemos resuelto un problema; todas ellas se han practicado suficientemente en la unidad 3. Fig. 26 El punto dado P es el que utilizamos como centro de inversión, siendo un valor cualquiera la razón de la misma. Con estos parámetros (Fig. 27), determinamos las circunferencias inversas de las dos circunferencias c y d iniciales. A las inversas c’ y d’ les trazamos, inicialmente, las rectas tangentes comunes exteriores; estas tangentes, T1’T2’ y T3’T4’, son las figuras inversas de dos de las circunferencias solución. Situamos sobre las circunferencias iniciales, y alineados con el centro P, los inversos de T1’, T2’, T3’ y T4’. Las rectas que unen cada punto de tangencia con el centro de la cir- Fig. 27 88 Generalización del estudio de tangencias APLICACIONES PRÁCTICAS UNIDAD cunferencia correspondiente son las que nos permiten encontrar los centros de las circunferencias solución: así, O1 se halla en la intersección entre la recta que une T1 con el centro de la circunferencia c y la recta que pasa, al mismo tiempo, por T2 y por el centro de la circunferencia d. Si una vez obtenidas las circunferencias c’ y d’, inversas de las iniciales, trazamos a las mismas las tangentes comunes interiores (Fig. 28), éstas nos permiten encontrar (siguiendo el mismo proceso empleado con las tangentes exteriores) las otras dos circunferencias tangentes a c y d pasando por el punto P. Fig. 28 • Circunferencias tangentes a otras dos y a una recta, CCR Deseamos trazar las circunferencias tangentes a las circunferencias c y d de la figura 29 y que lo sean, también, a la recta r de la misma figura. En los dos problemas de tangencias resueltos anteriormente, teníamos un punto que tomábamos como centro de inversión. Ahora no disponemos de ningún punto, pero restando el radio de la circunferencia pequeña, la d, a ella misma, ésta queda transformada en su centro. A los restantes ele- Fig. 29 89 4 UNIDAD 4 APLICACIONES PRÁCTICAS Generalización del estudio de tangencias mentos del problema aplicamos la misma transformación: así, la recta r se transforma en su paralela r’, pudiendo estar en cualquiera de los lados de ella, y la circunferencia c se transforma en otra circunferencia concéntrica y equidistante de ella una distancia igual al radio de la circunferencia d, también con la posibilidad de trazarla a uno u otro lado. De este modo, el problema inicial se nos ha transformado en trazar las circunferencias tangentes a una circunferencia y a una recta (las equidistantes de las c y r iniciales) pasando por un punto (el centro de la circunferencia d), problema que hemos denominado PCR y que resolvimos en las Aplicaciones prácticas de la unidad 3. Combinando la paralela a r a cada uno de sus lados con las circunferencias concéntricas a c, también a cada uno de sus lados, tenemos cuatro casos posibles PCR; cada uno de ellos tenía dos soluciones posibles, por lo que el problema planteado puede llegar a tener hasta ocho circunferencias solución que cumplan las condiciones iniciales. En la figura 30 hemos encontrado una de estas circunferencias tangentes a CCR mediante la realización simultánea de estas tres acciones: trazar la Fig. 30 90 Generalización del estudio de tangencias APLICACIONES PRÁCTICAS UNIDAD paralela inferior a la recta r, restar el radio a la circunferencia c y trazar las tangentes comunes exteriores a las dos circunferencias inversas de c’ y r’. La determinación de estas figuras inversas, así como pasar los puntos de tangencia sobre las circunferencias iniciales, se ha hecho en la forma acostumbrada, teniendo en cuenta que los puntos de tangencia se habrán de referir, finalmente, a la circunferencia c y a la recta r iniciales. Conocido el centro de la circunferencia solución, buscaremos el punto de tangencia en la circunferencia d mediante la recta de unión de sus centros. En la figura 31 trabajamos con los mismos elementos, pero con otra combinación: paralela inferior a la recta r, circunferencia concéntrica exterior a la circunferencia c y tangentes interiores a sus dos figuras inversas. Fig. 31 91 4 UNIDAD 4 APLICACIONES PRÁCTICAS Generalización del estudio de tangencias Dejamos el resto de combinaciones posibles como ejercicios optativos a realizar, teniendo en cuenta que, en función de la posición relativa entre los datos del problema, no siempre todas las soluciones posibles se concretan en soluciones reales. • Circunferencias tangentes a otras tres, CCC Este es el problema más complejo de tangencias: determinar las circunferencias tangentes, simultáneamente, a otras tres. El problema se ha de transformar para poder resolverlo mediante la aplicación de la inversión. La transformación consiste en restar el radio de la menor de las circunferencias; ésta queda transformada en su centro, que tomaremos como centro de inversión, mientras que las otras dos se transforman en circunferencias concéntricas a las iniciales y de radios iguales al propio, al que podremos añadir o restar el de la menor. El problema se ha transformado, por tanto, en trazar las tangentes a dos circunferencias pasando por un punto, caso que hemos denominado PCC y que hemos resuelto en el segundo apartado de 1.4. El problema tiene ocho circunferencias solución posibles. 2 TANGENCIAS CON OTRAS CÓNICAS Estudiadas las tangencias con circunferencias, en este apartado nos centraremos en las rectas tangentes a las restantes curvas cónicas: elipse, parábola e hipérbola. En todos los casos aplicaremos las propiedades que hemos visto en los Conocimientos teóricos. 2.1 Tangentes a la elipse Para el trazado de las tangentes a la elipse, no es necesario tener dibujada la cónica, nos basta con conocer sus ejes y la condición que ha de cumplir la tangente o tangentes que hemos de trazar, tangentes que agrupamos en los siguientes subapartados: • Recta tangente por un punto de la elipse Por un punto de la elipse, únicamente podemos trazar una tangente a la misma. Si unimos el punto P con los focos F y F’, la recta tangente es la bisectriz del ángulo formado por uno de los radios vectores, PF’, con la prolongación del otro, PF (Fig. 32). Fig. 32 92 Sobre la misma figura, y teniendo en cuenta que el simétrico de uno de los focos respecto a una recta tangente a la elipse se halla sobre la circunferencia focal del otro foco, hemos efectuado un trazado diferente. Generalización del estudio de tangencias APLICACIONES PRÁCTICAS 4 UNIDAD Representamos la circunferencia focal cuyo centro es el foco F y unimos este foco con el punto P; la prolongación del radio vector intercepta sobre la circunferencia focal el punto M; la mediatriz de MF’ es la tangente buscada. • Rectas tangentes desde un punto exterior a la elipse A partir de los ejes AB y CD, determinamos los focos F y F’. Con centro en el punto dado P, trazamos una circunferencia que pase por F y, con centro en el otro foco F’, trazamos la circunferencia focal correspondiente; la intersección de ambas circunferencias se produce en los puntos 1 y 2 de la figura 33. Las mediatrices de los segmentos 1F y 2F son las tangentes buscadas. El punto de contacto con la elipse de cada una de las tangentes trazadas se halla uniendo los puntos 1 y 2 con el foco F’; estas rectas cortan a cada una de las tangentes en los puntos T y T’. • Rectas tangentes paralelas a una dirección dada Con centro en uno de los focos, trazamos la circunferencia focal correspondiente y, desde el otro foco, dibujamos la recta perpendicular a la dirección dada. Circunferencia y recta se cortan en dos puntos, 1 y 2, de la figura 34; las mediatrices de los segmentos 1F y 2F son las tangentes buscadas. Los puntos de tangencia T1 y T2, se hallan en la intersección de las rectas 1F’ y 2F’ con la tangente correspondiente. Golden Gate. San Francisco, California. Fig. 33 Fig. 34 93 UNIDAD 4 APLICACIONES PRÁCTICAS Generalización del estudio de tangencias 2.2 Tangentes a la parábola Como en la elipse, no es necesario tener dibujada una parábola para trazar rectas tangentes a ella, basta conocer su foco y directriz, u otros elementos que permitan su determinación. Veamos casos similares a los vistos en la anterior cónica. • Recta tangente por un punto de la parábola Fig. 35 Desde el punto P (Fig. 35), trazamos la perpendicular a la directriz para unir el punto M, en que esta perpendicular la corta, con el foco F; la mediatriz del segmento FM coincide con la tangente a la parábola por el punto P. La tangente es, lógicamente, bisectriz del ángulo MPF. • Rectas tangentes desde un punto exterior a la parábola Trazamos una circunferencia que, con centro en el punto P, pase por el foco F de la parábola (Fig. 36). Esta circunferencia corta la directriz en los puntos 1 y 2, los cuales, por ser los simétricos del foco respecto a cada una de las tangentes, permiten la determinación de las mismas. Las mediatrices de los segmentos 1F y 2F son las tangentes solicitadas; sobre ellas, trazando la perpendicular a la directriz desde los puntos 1 y 2, encontraremos los correspondientes puntos de tangencia T1 y T2. • Rectas tangentes paralelas a una dirección dada Fig. 36 Desde el foco trazamos una perpendicular a la dirección d dada (Fig. 37), perpendicular que se corta con la directriz en el punto M. Este punto, por estar en la directriz, es el simétrico del foco respecto a una de las tangentes, por lo que ésta será la mediatriz del segmento FM. Fig. 37 94 Generalización del estudio de tangencias APLICACIONES PRÁCTICAS 4 UNIDAD 2.3 Tangentes a la hipérbola Con el eje AB y la distancia focal FF’, tenemos definida una hipérbola a la que podemos trazar rectas tangentes en los siguientes supuestos: • Recta tangente por un punto de la hipérbola Como ocurría en la elipse, la tangente a una hipérbola por uno de sus puntos, hipérbola no dibujada de la figura 38, es la bisectriz del ángulo formado por los dos radios vectores que unen el punto P con los focos de la hipérbola, segmentos PF y PF’. Fig. 38 • Rectas tangentes desde un punto exterior a la hipérbola Haciendo centro en el punto P y con radio igual a su distancia hasta uno de los focos, trazamos una circunferencia que se corta en los puntos 1 y 2 con la circunferencia focal del otro foco (Fig. 39). Los puntos 1 y 2 son los simétricos del foco F respecto a sendas rectas tangentes a la hipérbola; por tanto, las tangentes buscadas serán las mediatrices de los segmentos 1F y 2F. Sobre ellas, y en su intersección con las rectas que unen los puntos 1 y 2 con el centro de la circunferencia focal, se hallan los puntos de tangencia con la hipérbola T1 y T2. • Rectas tangentes paralelas a una dirección dada Fig. 39 Desde uno de los focos trazamos la perpendicular a la dirección d dada, buscando sus puntos de corte, 1 y 2 en la figura 40, con la circunferencia focal correspondiente al otro foco. Las mediatrices de los segmentos 1F’ y 2F’ son las tangentes buscadas. Fig. 40 95 UNIDAD 4 CUESTIONES Y EJERCICIOS Generalización del estudio de tangencias Tangencias con circunferencias 1. Como aplicación de los elementos radicales, trazar las circunferencias tangentes a la de la figura 41 que, pasando por el punto P, también lo sean a la recta r. 5. Trazar las circunferencias tangentes a las rectas r y s que pasen por el punto P (Fig. 45). Fig. 45 Fig. 41 2. Trazar las circunferencias tangentes a la recta y circunferencia de la figura 42 que pasen por el punto P. Fig. 42 3. Determinar las circunferencias que, pasando por los puntos A y B de la figura 43, sean tangentes a la recta r. Fig. 43 4. Determinar las circunferencias tangentes a las rectas de la figura 44 que pasen por el punto P de la misma. 6. Determinar las circunferencias tangentes, simultáneamente, a las rectas r y s y a la circunferencia de centro O (Fig. 46). Fig. 46 7. Trazar las circunferencias que, pasando por el punto P de la figura 47, sean tangentes a la recta y circunferencia de la misma figura. Fig. 47 8. Representar alguna de las circunferencias que, pasando por el punto P, sean tangentes, simultáneamente, a las de la figura 48. Fig. 48 Fig. 44 96 Generalización del estudio de tangencias CUESTIONES Y EJERCICIOS UNIDAD 9. Buscar alguna de las circunferencias tangentes, simultáneamente, a las tres circunferencias de la figura 49. Fig. 49 10. Dibujar las figuras de los croquis, con las medidas indicadas sobre los mismos, determinando con precisión los diferentes centros y puntos de tangencia (Fig. 50 y 51). Fig. 52 Fig. 50 Fig. 53 Tangencias con cónicas 12. Los segmentos AB y CD de la figura 54 definen una elipse; trazar la tangente a la misma desde el punto P; determinar los puntos de tangencia sobre cada una de las tangentes trazadas. Fig. 51 11. Como en la actividad anterior, trazar las figuras indicadas en los croquis correspondientes (Fig. 52 y 53). Fig. 54 97 4 UNIDAD 4 CUESTIONES Y EJERCICIOS Generalización del estudio de tangencias 13. Trazar las tangentes a la elipse, representada por los elementos dados en la figura 55, paralelas a la dirección d. Hallar los puntos de tangencia sobre cada recta tangente. 16. Determinar los puntos de tangencia de las rectas t1 y t2 con la parábola cuyo foco es el punto F de la figura 58. Fig. 58 Fig. 55 14. Construir la elipse de la que conocemos su eje AB y una de las tangentes a la cónica (Fig. 56). Fig. 56 17. Trazar las tangentes a la hipérbola representada por los vértices y focos dados en la figura 59, que pasan por el punto P. Hallar los puntos de tangencia sobre cada recta tangente. Fig. 59 15. Trazar las tangentes a la parábola que definen la directriz y el foco dados en la figura 57, desde un punto P exterior a la cónica. Fig. 57 Contenidos básicos de la unidad en formato hipermedia, en el CD. Más actividades en el CD La inspiración existe, pero tiene que encontrarte trabajando. PABLO PICASSO 98