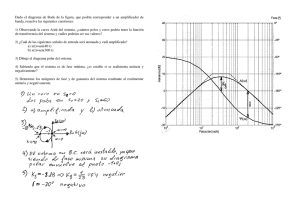
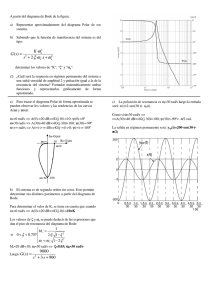
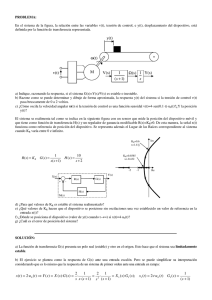
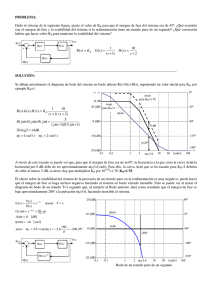
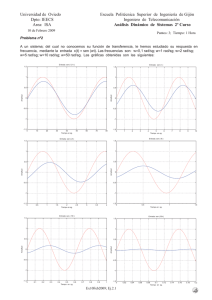
En la figura se representan los diagramas de Bode de... y G2(s), y sus correspondientes diagramas polares.

En la figura se representan los diagramas de Bode de dos sistemas de fase mínima, G1(s)
y G2(s), y sus correspondientes diagramas polares.
a)
3
a) Determine el diagrama de bode y el diagrama polar del sistema G3(s) resultado
de poner en cascada los sistemas G(1) y G(2).
G3(s)
X(s)
Y(s)
G1(s)
G2(s)
III
10 [dB]
90º
Im
ψ(ω)
0 [dB]
45º
ω=0
0º
-10 [dB]
b) ¿Cuál es la respuesta del sistema G3(s) en régimen permanente ante una señal
de entrada x(t) = sen(0.1·t) + sen(t+π/4)?
A(ω)
Re
-45º
-20 [dB]
ω=∞
1
I
10 [dB]
0 [dB]
A(ω)
Im
45º
ω=∞
-10 [dB]
-30 [dB]
0.01
ψ(ω)
1
[rad/s]
-90º
10
b) A partir de diagrama de Bode de G3(s):
ω=0
Re
-45º
-30 [dB]
0.01
A(0.1) = A(1) = -10 dB ; ψ(0.1) = π/4 ; ψ(1) = -π/4
0º
-20 [dB]
0.1
1
[rad/s]
II
90º
ψ(ω)
Im
0 [dB]
45º
-10 [dB]
0º
ω=0
ω=∞
A(ω)
Re
-20 [dB]
-45º
0.1
1
[rad/s]
-90º
10
yRP(t) = 10-10/20·sen(0.1·t+π/4) + 10-10/20·sen(t+π/4-π/4)
yRP(t) = 0.32·sen(0.1·t+π
π/4) + 0.32·sen(t)
-90º
10
2
10 [dB]
-30 [dB]
0.01
0.1
90º