Ley de Gauss 1. Una esfera de radio

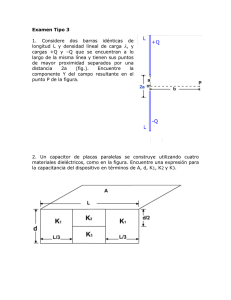
Ley de Gauss
1. Una esfera aislante de radio a tiene una densidad de carga uniforme  y una carga
positiva total Q. Calcule la magnitud del Campo Eléctrico en un punto:
a. Fuera de la esfera (r > a)
b. Dentro de la esfera a una distancia r < a
6
+++++++
m
+++++ r ++
+
+++++++ r>a
+ + + + ++ a + +
+ + +++ + +
+
2. Un cascarón esférico delgado de radio a tiene una carga total Q distribuida
uniformemente sobre su superficie. Encuentre la magnitud del campo eléctrico en
puntos dentro y fuera del cascarón
3. Una esfera conductora sólida de radio a tiene una carga positiva neta 2Q. Una cascarón
esférico conductor de radio interior b y radio exterior c es concéntrico con la esfera
sólida y tiene una carga neta –Q. Determine la magnitud del campo eléctrico en los
puntos marcados (ver figura), así como la distribución de carga sobre el cascarón
esférico.
2
Q
a
-Q
2Q
c
b
4. Una pirámide con una base cuadrada de 6m y altura de 4m se coloca en una campo
eléctrico vertical de 52 N/C.
a. Calcule el flujo eléctrico a través de una de las caras.
b. Multiplique el flujo encontrado por 4 y compruebe su resultado calculando el
flujo total a través de la base de la pirámide.
4m
6m
5. Un cable coaxial largo se compone de un conductor cilíndrico interior de radio a y un
cilindro coaxial exterior de radio interior b y radio exterior c. El cilindro exterior esta
montado sobre soportes aislantes y no tiene carga neta, El cilindro interior tiene una
carga positiva uniforme en cada unidad de longitud . Calcule el campo eléctrico:
a. En cualquier punto entre los cilindros, a una distancia r del eje
b. En cualquier punto afuera del cilindro exterior
c. Grafique la magnitud del campo eléctrico en función de la distancia r respecto al
eje del cable, de r = 0 a r = 2c
d. Halle la carga en cada unidad de longitud de la superficie interna y en la
superficie externa del cilindro exterior