Curso 04/05 (Convocatoria de Junio)

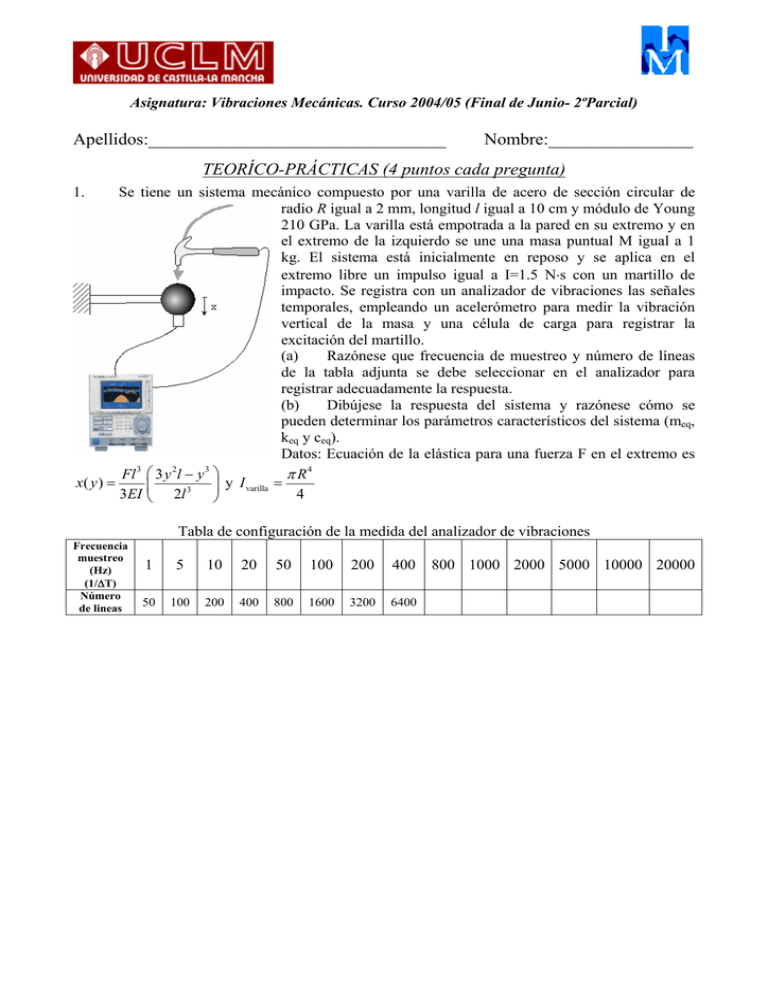
Asignatura: Vibraciones Mecánicas. Curso 2004/05 (Final de Junio- 2ºParcial)
Apellidos:_________________________________
Nombre:________________
TEORÍCO-PRÁCTICAS (4 puntos cada pregunta)
1.
Se tiene un sistema mecánico compuesto por una varilla de acero de sección circular de
radio R igual a 2 mm, longitud l igual a 10 cm y módulo de Young
210 GPa. La varilla está empotrada a la pared en su extremo y en
el extremo de la izquierdo se une una masa puntual M igual a 1
kg. El sistema está inicialmente en reposo y se aplica en el
extremo libre un impulso igual a I=1.5 N⋅s con un martillo de
impacto. Se registra con un analizador de vibraciones las señales
temporales, empleando un acelerómetro para medir la vibración
vertical de la masa y una célula de carga para registrar la
excitación del martillo.
(a)
Razónese que frecuencia de muestreo y número de líneas
de la tabla adjunta se debe seleccionar en el analizador para
registrar adecuadamente la respuesta.
(b)
Dibújese la respuesta del sistema y razónese cómo se
pueden determinar los parámetros característicos del sistema (meq,
keq y ceq).
Datos: Ecuación de la elástica para una fuerza F en el extremo es
3
2
3
π R4
Fl  3 y l − y 
y
I
=
x( y ) =


varilla
4
3EI  2l 3 
Tabla de configuración de la medida del analizador de vibraciones
Frecuencia
muestreo
(Hz)
(1/∆T)
Número
de lineas
1
5
10
20
50
100
200
400
50
100
200
400
800
1600
3200
6400
800 1000 2000 5000 10000 20000
2. Se tiene una sistema mecánico compuesto por una varilla rígida uniforme de masa 2m y longitud
L colgada por sus extremos de con dos resortes de rigidez k. Los resortes están unidos a dos masas
puntuales iguales de valor m que solo pueden moverse en dirección vertical según se muestra en la
figura. Cada una de las masas puntuales están colgada del techo por
unos resorte de rigidez k. Si la posición de la figura es la de equilibrio
estático, obténgase:
(a) Número de grados de libertad del sistema y vector de
desplazamiento escogido para el estudio. Dibújese las variables del
vector en un dibujo.
(b) Ecuaciones dinámicas del sistema para el estudio de las
vibraciones libres.
(c) Matrices de masa y rigidez.
PROBLEMA nº1 (6 Puntos)
Se tiene un sistema mecánico compuesto por un carrito que se desplaza en un plano
horizontal y una varilla de longitud L, ambos
tienen una masa m y están acoplados con
resortes de rigidez k según se muestra en la
figura. Determínese:
(a) Ecuaciones dinámicas del sistema para el
estudio de las vibraciones libres.
(b) Frecuencias naturales y modos de vibración
del sistema.
Datos: m=1kg, L=1 m y k=1000N/m.
PROBLEMA Nº2 (6 Puntos)
Se tiene un ventilador centrífugo que posee un elevado nivel de vibraciones. El ventilador se
acciona mediante un motor con una transmisión por correas según se muestra en la figura. Para
detectar la causa de este nivel anormal se efectúa un análisis en frecuencia midiendo la vibración
sobre un rodamiento del ventilador y en dirección vertical, en la gráfica adjunta se muestra el
espectro medido. En función de los datos constructivos, razonar justificadamente cuáles son los
defectos que sufre la máquina.
Características técnicas
Motor: potencia 18.5 kW, giro a 1000 rpm
Polea lado motor: diámetro 40 cm
Polea lado ventilador: diámetro 25 cm
Correa de longitud 200 cm
Número de palas=12
Rodamientos de motor y ventilador:
Diámetro de bolas: 6 mm
Número de bolas: 12
Diámetro pista interior: 28 mm
Diámetro pista exterior: 34 mm
Angulo de contacto: 0º
2.0
1.8
1.6
1.4
mm/s
1.2
1.0
0.8
0.6
0.4
0.2
0.0
0
25
50
75
100
125
150
175
200
225
250
Hz
Formulas de frecuencias de fallo de rodamientos:
D
Do
Di
f bola = i
f bext =
N bω
ω
Db Do + Di
Do + Di
f bint =
Do
N bω
Do + Di
f jaula =
Di
ω
Do + Di
Asignatura: Vibraciones Mecánicas. Curso 2004/05 (Final de Junio. 1er Parcial)
Apellidos:_________________________________
Nombre:________________
TEORÍCO-PRÁCTICAS (12 puntos)
Formulas necesarias para la resolución del examen:
Función
Módulo
1
1
M (ω ) =
M (ω ) =
2
(1 − τ 2 ) + i 2ζτ
(1 − τ 2 ) + ( 2ζτ )2
1 + i 2ζτ
T (ω ) =
(1 − τ 2 ) + i 2ζτ
T (ω ) =
Z
τ2
=
Y (1 − τ 2 ) + i 2ζτ
Z
=
Y
1.
1 + ( 2ζτ )
ϕ = arctg
2
(1 − τ ) + ( 2ζτ )
2 2
τ2
(1 − τ ) + ( 2ζτ )
2 2
Desfase
2
2
ϕ = arctg
2ζτ
1−τ 2
2ζτ 3
1 − τ 2 + 4ζ 2τ 2
ϕ = arctg
Máximo
ωr = ωn 1 − 2ζ
(1 + 8ζ )
2
ωr = ωn
4ζ
1
2
2ζτ
1−τ 2
Se tiene el sistema mecánico de la figura, compuesto por una masa m, un muelle de rigidez k y
un amortiguador viscoso de coeficiente de amortiguamiento c.
x
El sistema se encuentra originalmente en reposo, si desplaza
de su oposición de equilibrio una distancia X positiva y se deja
c
vibrar libremente. Escribir las posibles ecuaciones de la
m
respuesta x(t) en función del amortiguamiento c explicando los
términos que aparecen. Cada solución de deberá acompañar
k
con su correspondiente representación en función del tiempo.
2
2
−1
2. En la figura se muestra un sistema mecánico compuesto por dos masas puntuales
unidas por un brazo de masa despreciable, el brazo
tiene un resorte a torsión kt. La masa m1 está unida al
suelo por medio de tres resortes montados dos en serie
y en paralelo con el restante, tal y como se muestra en
la figura. La masa m2 está unida a una varilla que tiene
en su extremo una boya de masa m y área A que flota
en un líquido de densidad ρ. Las dimensiones
necesarias para resolver el problema son las que se
muestran en el dibujo. Suponiendo que las varillas y
brazos son rígidos. Obténgase:
(a) Sistema equivalente de un grado de libertad para el
giro del brazo (coordenada ϑ).
(b) Frecuencia natural del sistema.
3. Se tiene un eje de acero de 1 m de longitud con módulo de Young E=210 GPa y diámetro 50 mm,
con ambos extremos está apoyado con un
rodamiento de bolas. Tiene acoplado un rotor de
masa m igual a 100 kg en la mitad del eje. La
máquina funciona en el rango de 0 a 3000 rpm.
Determinar la frecuencia crítica del eje.
Ecuación de la elástica: y ( x ) =
Momento de inercia: I =
πd4
64
F  xb 2
3
l − x 2 − b 2 ) + x − a  (Nota: término x − a para x≥a)
(

6 EI  l

4. En una planta industrial se tiene una máquina de precisión que funciona incorrectamente por el
excesivo nivel de vibraciones que se transmiten por el suelo. Se decide instalar unos absorsores de
vibración para reducir el nivel de vibraciones. Dibujar la curva que se debería emplear para la
selección, describiendo el proceso que se debe seguir. ¿Cómo debe ser el coeficiente de
amortiguamiento relativo del absorsor?
PROBLEMA (8 Puntos)
Se tiene una varilla rígida esbelta de longitud L=1 m y masa M=10 kg, articulada en el extremo
inferior. En el extremo superior está acoplado un resorte de
rigidez k y un amortiguador viscoso de coeficiente de
amortiguamiento c. En el lado izquierdo tiene un resorte de
rigidez k acoplado en el centro de masas. Determinar:
(a) Rigidez torsional equivalente, frecuencia natural y
coeficiente de amortiguamiento relativo para el estudio de las
vibraciones torsionales de la varilla.
(b) La respuesta (permanente y transitoria) del sistema si un
actuador comienza a funcionar aplicando una fuerza en el
centro de masas igual a F(t)=F0senωt con F0=2000 N.
Inicialmente la varilla está en reposo.
(c) Frecuencia de excitación donde el desplazamiento angular
es máximo y distancia D que debe existir entre la varilla en
posición vertical y la pared de la izquierda para que la varilla
no impacte en estas condiciones.
Datos:
k=100 N/mm, c=100 Ns/m