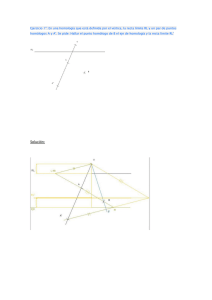
Para que una homología quede determinada es preciso conocer

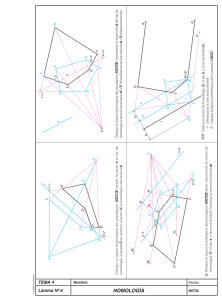
DETERMINACIÓN DE UNA HOMOLOGÍA.
O
Para que una homología quede determinada es preciso conocer, además
de una de las figuras, los siguientes elementos:
A
B
El eje, el centro y el punto homólogo cualquiera de la figura dada.
C
EJE
(Ilustración nº 4)
Para obtener la transformada se debe aplicar el método empleado en la
ilustración nº 2.
En la ilustración nº 4 partimos de un triángulo dado ABC y un punto
A'
homólogo A’, para obtener el triángulo transformado se trazan rectas
O
desde el centro de homología O por cada uno de los vértices del triángulo (A..B..C) y se prolonga el lado ABe hasta que corten al eje de simetría en un punto. Al unir dicho punto con el homólogo de A (A’)
A
B
mediante una recta ésta cortará a la trazada por O y B en un punto B’
C
EJE
que será homólogo de B.
C'
La figura se completa prolongando otro lado (BC o AC) hasta que corte
al eje de simetría y aplicando lo anterior.
B'
A'
ILUSTRACIÓN Nº 4
El eje, el centro y la recta límite de la figura dada, (Ilustración nº 5)
O
En este caso se debe aplicar de forma inversa el procedimiento seguido
para la obtención de rectas límites (ilustración nº 3).
RL
En la ilustración nº 5 se ha hallado el transformado de un triángulo ABC
a partir de una recta límite su eje y centro de homología
A
B
1º) Desde el centro de homología (O) trazar rectas que pasen por
los vértices del triángulo dado (ABC).
C
EJE
2º) Prolongar uno de los lados (AC) del triángulo dado hasta que
corte a la recta límite dada en un punto (M), unir dicho punto
con el centro de homología (O).
O
RL
N
M
A
4º) Repetir los pasos 2 y 3 con el lado BC o AB y completar la
transformada.
B
EJE
3º) Prolongar el mismo lado (AC) hasta cortar en un punto al eje
de homología y por dicho punto trazar una paralela al segmento
OM hasta que corte a las rectas trazadas desde O y que pasen
por los puntos A y C obteniendo así los homólogos A’ y C’.
C
C'
B'
5º) La figura también se puede resolver si prolongamos Ab hasta
que corte al eje de simetría en un punto y unimos mediante una
recta éste con el homólogo de A (A’) anteriormente hallado,
esta recta cortará a la recta que pase por O y B en un punto B’.
Obsérvese como los segmentos OM y A’C’ son paralelos así como ON
y C’B’.
A'
ILUSTRACIÓN Nº 5