HOMOLOGÍA

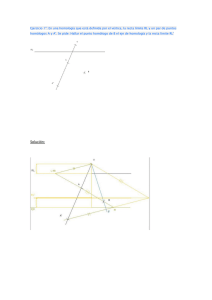
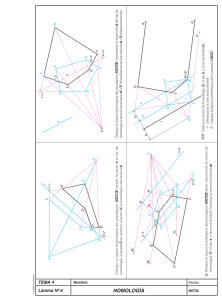
HOMOLOGÍA
DEFINICIÓN Y GENERALIDADES.
La homología es una transformación geométrica de una figura en otra coplanarias, de manera que se correspondan
punto a punto y recta a recta respetando las siguientes leyes: (Ilustración 1).
O
O
RECTA LÍMITE
A
A
B
C
C
EJE
A'
C'
B
C'
B'
B'
A'
ILUSTRACIÓN Nº 1
Dos puntos homólogos (A y A’) están alineados con un punto fijo (O) llamado centro de homología.
Dos rectas homólogas se cortan en una recta llamada eje de homología.
R.L
C
A'
d
B
C'
EJ
E
B'
O
RL
N
M
d
C'
A
R' L'
B P
d
C
EJE
C'
B'
A'
ILUSTRACIÓN Nº 2
d
EJE
R' L'
RL
R' L'
EJE
ILUSTRACIÓN Nº 3
d
O
d
O
RL
d
* Puntos Homólogos: Son los que corresponden a la pareja de puntos formada por el inicial (A) y su transformado (A’). (Ilustración nº 2).
N
A
*Centro de Homología: Es el punto de convergencia de las rectas que contienen a un punto y a su homólogo.
* Eje de Homología: Es la recta doble formada por puntos que son homólogos de ellos mismos.
* Rectas límite: Son las rectas que definen el lugar geométrico de los puntos
homólogos del infinito que corresponden a las figuras inicial y transformada.
Siendo una homología una relación entre dos figuras, existen dos rectas límite, una por cada figura. (Ilustración 2)
La distancia (d) de una recta límite respecto al centro de homología es igual
a la distancia de la otra recta límite respecto al eje de homología.(Ilustración
nº 2). Para determinar las rectas límites se sigue el siguiente método:
(Ilustración nº2).
Para la figura original (ABC): Por el centro de homología se traza una recta
paralela a un lado homólogo (A’C’) y se prolonga el lado original (AC) hasta que corte a la paralela anterior en un punto (M). Para obtener otro punto
de la recta límite se sigue el mismo procedimiento: por O se traza una paralela a C’B’ y se prolonga el lado original CB hasta que ambos se corte en N.
Se unen los puntos hallados anteriormente (M y N) mediante una recta, que
resulta paralela al eje de homología, obteniendo así la recta límite.
La recta límite de la figura transformada (A’B’C’) se determina siguiendo el
mismo método aplicado a su homóloga (A’B’C’).
Como las rectas límites son siempre paralelas al eje de homología, también
serán paralelas entre sí, además se puede comprobar en la ilustración nº 3
que la distancia entre una recta límite y el centro de homología es igual a la
distancia que existe entre la otra recta límite y el eje, pudiendo ocupar las
dos posiciones indicadas en la ilustración nº 3.
O
M