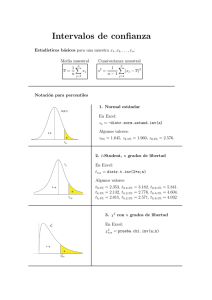
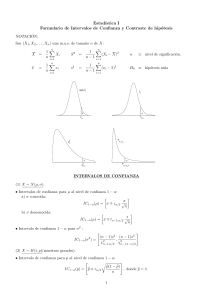
NOTACI ´ON: (X1,...,Xn) muestra aleatoria de X: ¯x = 1 n ∑ xi 1 n − 1

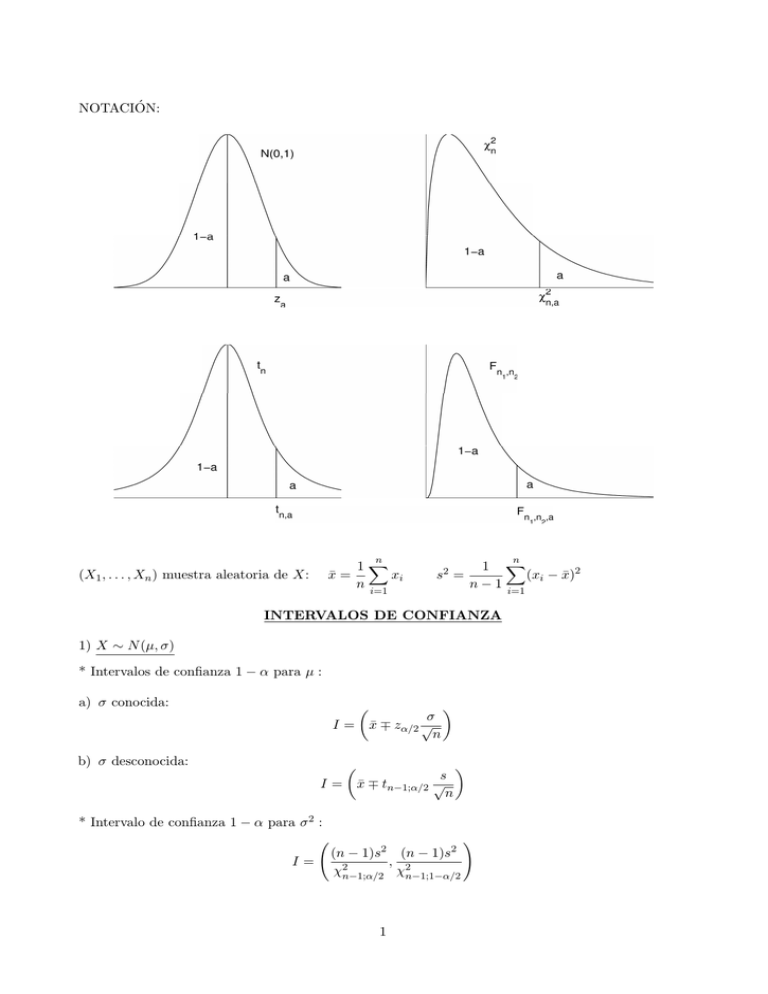
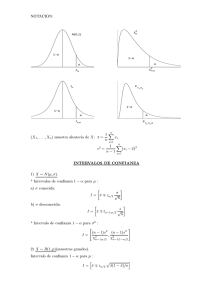
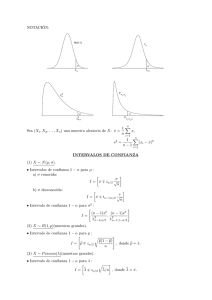
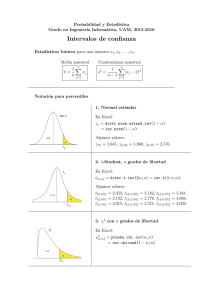
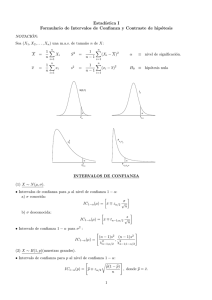
NOTACIÓN:
n
(X1 , . . . , Xn ) muestra aleatoria de X:
x̄ =
1X
xi
n
n
s2 =
i=1
1 X
(xi − x̄)2
n−1
i=1
INTERVALOS DE CONFIANZA
1) X ∼ N (µ, σ)
* Intervalos de confianza 1 − α para µ :
a) σ conocida:
σ
I = x̄ ∓ zα/2 √
n
b) σ desconocida:
I=
s
x̄ ∓ tn−1;α/2 √
n
* Intervalo de confianza 1 − α para σ 2 :
I=
(n − 1)s2 (n − 1)s2
,
χ2n−1;α/2 χ2n−1;1−α/2
1
!
2) X ∼ Bernoulli(p)(muestras grandes)
Intervalo de confianza 1 − α para p :
r
x̄ ∓ zα/2
I=
x̄(1 − x̄)
n
!
3) Intervalo de confianza para la media µ de una población no necesariamente normal (muestras grandes)
s
I = x̄ ∓ zα/2 √
n
4) Dos poblaciones normales independientes
X ∼ N (µ1 , σ1 ); (X1 , . . . , Xn1 ) m. a. de X; se calcula x̄ y s21 .
Y ∼ N (µ2 , σ2 ); (Y1 , . . . , Yn2 ) m. a. de Y ; se calcula ȳ y s22 .
s2p =
(n1 − 1)s21 + (n2 − 1)s22
n1 + n2 − 2
* Intervalos de confianza 1 − α para µ1 − µ2 :
a) σ1 , σ2 desconocidas, σ1 = σ2 :
r
I=
x̄ − ȳ ∓ tn1 +n2 −2;α/2 sp
1
1
+
n1 n2
b) σ1 , σ2 desconocidas, σ1 6= σ2 :

s
I = x̄ − ȳ ∓ tf ;α/2

s21
s22 
+
n1 n2
donde f es el entero más próximo a
(s21 /n1 + s22 /n2 )2
(s21 /n1 )2
n1 −1
+
(s22 /n2 )2
n2 −1
* Intervalo de confianza 1 − α para σ12 /σ22 :
s21 /s22
s21
, F
I=
Fn1 −1,n2 −1;α/2 s22 n2 −1,n1 −1;α/2
5) Comparación de proporciones (muestras grandes e independientes)
X ∼ B(1, p1 ); (X1 , . . . , Xn1 ) m. a. de X
Y ∼ B(1, p2 ); (Y1 , . . . , Yn2 ) m. a. de Y
Intervalo de confianza 1 − α para p1 − p2 :

I = x̄ − ȳ ∓ zα/2
s

x̄(1 − x̄) ȳ(1 − ȳ) 
+
n1
n2
2
CONTRASTES DE HIPÓTESIS
NOTACION:
α = nivel de significación del contraste
n = tamaño de la muestra
H0 = hipótesis nula
R = región crı́tica o de rechazo de H0
1) X ∼ N (µ, σ)
s
R = |x̄ − µ0 | > tn−1;α/2 √
n
s
R = x̄ − µ0 > tn−1;α √
n s
R = x̄ − µ0 < tn−1;1−α √
n
∈
/ χ2n−1;1−α/2 , χ2n−1;α/2
2
> χn−1;α
2
< χn−1;1−α
H0 : µ = µ0 (σ desconocida);
H0 : µ ≤ µ0 (σ desconocida);
H0 : µ ≥ µ0 (σ desconocida);
n−1 2
H0 : σ = σ0 ; R =
2 s
σ0
n−1 2
H0 : σ ≤ σ0 ; R =
2 s
σ0
n−1 2
H0 : σ ≥ σ0 ; R =
s
σ02
2) X ∼ Bernoulli(p) (muestras grandes)
(
)
r
p0 (1 − p0 )
H0 : p = p0 ; R = |x̄ − p0 | > zα/2
n
(
)
r
p0 (1 − p0 )
H0 : p ≤ p0 ; R = x̄ − p0 > zα
n
)
(
r
p0 (1 − p0 )
H0 : p ≥ p0 ; R = x̄ − p0 < z1−α
n
(tn−1;1−α = −tn−1;α )
(z1−α = −zα )
3) Contrastes para la media de una población no necesariamente normal (muestras grandes)
s
H0 : µ = µ0 (σ desconocida);
R = |x̄ − µ0 | > zα/2 √
n
s
H0 : µ ≤ µ0 (σ desconocida);
R = x̄ − µ0 > zα √
n s
H0 : µ ≥ µ0 (σ desconocida);
R = x̄ − µ0 < z1−α √
(z1−α = −zα )
n
4) Dos poblaciones normales independientes
X ∼ N (µ1 , σ1 ); (X1 , . . . , Xn1 ) m. a. de X; se calcula x̄ y s21 .
Y ∼ N (µ2 , σ2 ); (Y1 , . . . , Yn2 ) m. a. de Y ; se calcula ȳ y s22 .
(n1 − 1)s21 + (n2 − 1)s22
n1 + n2 − 2
r
1
1
R = |x̄ − ȳ| > tn1 +n2 −2;α/2 sp
+
n1 n2


s

s21
s2 
R = |x̄ − ȳ| > tf ;α/2
+ 2

n1 n2 
r
1
1
R = x̄ − ȳ > tn1 +n2 −2;α sp
+
n1 n2
s2p =
H0 : µ1 = µ2 (σ1 = σ2 );
H0 : µ1 = µ2 (σ1 6= σ2 );
H0 : µ1 ≤ µ2 (σ1 = σ2 );
3
H0 : µ1 ≤ µ2 (σ1 6= σ2 );
H0 : µ1 ≥ µ2 (σ1 = σ2 );
H0 : µ1 ≥ µ2 (σ1 6= σ2 );
s21
2
s22
s1
R=
2
s22
s1
R=
s22
H0 : σ1 = σ2 ;
H0 : σ1 ≤ σ2 ;
H0 : σ1 ≥ σ2 ;
R=


s

s22 
s21
+
R = x̄ − ȳ > tf ;α

n1 n2 
r
1
1
R = x̄ − ȳ < tn1 +n2 −2;1−α sp
+
n1 n2


s

s21
s2 
R = x̄ − ȳ < tf ;1−α
+ 2

n1 n2 
∈
/ Fn1 −1;n2 −1;1−α/2 , Fn1 −1;n2 −1;α/2
> Fn1 −1;n2 −1;α
< Fn1 −1;n2 −1;1−α
donde f = entero más próximo a
(s21 /n1 + s22 /n2 )2
(s21 /n1 )2
n1 −1
+
(s22 /n2 )2
n2 −1
ANÁLISIS DE LA VARIANZA (ANOVA)
Rechazamos la hipótesis de igualdad de medias H0 : µ1 = . . . = µI , al nivel de significación α,
cuando
PI
2
i=1 ni (ȳi• − ȳ•• )
F = PI PnI − 1
> FI−1;n−I;α
2
i
j=1 (yij − ȳi• )
i=1
n−I
Tabla ANOVA:
Fuentes de
variación (FV)
Explicada o
Entre grupos
Suma de
cuadrados (SC)
I
X
SCE =
ni (ȳi• − ȳ•• )2
Grados de
libertad (gl)
Varianzas o Cuadrados
medios (CM)
I −1
s2e =
SCE
I −1
(yij − ȳi• )2
n−I
s2R =
SCR
n−I
(yij − ȳ•• )2
n−1
i=1
Residual o
Dentro de los grupos
SCR =
Total
SCT =
ni
I X
X
i=1 j=1
ni
I X
X
i=1 j=1
4
Estadı́stico
F