[1library.co] análisis de sistemas y señales transformadas de laplace z y fourier índice transformadas de laplace

Análisis de Siste
S emass y Señalles
Transfo
ormadass: Laplacce, Z y Fourier.
F
F
L
Z
A
Alumnos:
ƒ
ƒ
ƒ
ƒ
ƒ
Anzurres Robles Jorrge
Garcíaa Luciano Lau
ura
Queza
ada Borja Arn
nulfo
Rojas Arteaga I. Karina
Román Guadarram
ma José Roquee
G
Grupo:
04
F
Fecha
de entrega: 12‐Marzzo.2008
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
ÍNDICE
Transformadas de Laplace……………………………………………………………………………………………….
ƒ
ƒ
ƒ
ƒ
ƒ
ƒ
Pulso
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Impulso ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Escalón ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Exponencial [Decreciente y creciente] ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Senoidal ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Rampa ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
3
4
4
5‐6
6
8
Transformada de Fourier………………………………………………………………………………………………….
ƒ
ƒ
ƒ
ƒ
ƒ
ƒ
Pulso
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Impulso ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Escalón ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Exponencial [Decreciente y creciente] ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Senoidal ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Rampa ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Pulso
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Impulso ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Escalón ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Exponencial [Decreciente y creciente] ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Senoidal ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Rampa ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
9
9
10
10
10‐11
11
12
Transformada Z…………………………………………………………………………………………………………………
ƒ
ƒ
ƒ
ƒ
ƒ
ƒ
3
14
14
14
15
15
16
17
Bibliografía……………………………………………………………………………………………………………………..
18
2
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
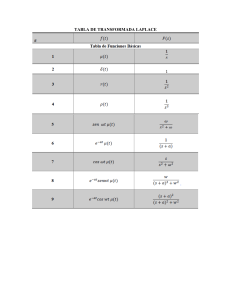
Transformada de Laplace
La Transformada de Laplace de una función f(t) para todos los números reales t ≥ 0 es la función F(s),
definida por:
Siempre y cuando la integral esté definida.
Esta transformada integral tiene una serie de propiedades que la hacen útil en el análisis de sistemas
lineales. Una de las ventajas más significativas radica en que la integración y derivación se convierten en
multiplicación y división.
Una aplicación importante en los sistemas lineales es el cálculo de la señal de salida. Ésta se puede calcular
mediante la convolución de la respuesta impulsiva del sistema con la señal de entrada. La realización de este
cálculo en el espacio de Laplace convierte la convolución en una multiplicación, habitualmente más sencilla.
La transformada de Laplace toma su nombre en honor de Pierre‐Simon Laplace.
Cuando se habla de la transformada de Laplace, generalmente se refiere a la versión unilateral. También
existe la transformada de Laplace bilateral, que se define como sigue:
La transformada de Laplace F(s) típicamente existe para todos los números reales s > a, donde a es una
constante que depende del comportamiento de crecimiento de f(t).
Calculando las transformadas de Laplace de las funciones elementales:
ƒ
Pulso
Sea la función impulso siguiente:
Donde A y T0 son constantes y cuya gráfica es:
La transformada de esta función se calcula de la siguiente manera:
3
Análisis de Sistemas y Señales: Transforrmadas de Laplaace, Z y Fourier.
ƒ
Impulso
∞
Usando la propiedad:
∫ ∂(t − t ) f (t ) = f (t )
0
0
−∞
L=
ƒ
0
1
Escalón
La función escalón un
nitario o funció
ón de Heavisidee H:[0, +∞]
se define com
mo:
Teniend
do la función f (t‐0) que simp
plificado tenem
mos sólo f(t) no
os quedaría la ecuación
e
de la siguiente
maneraa:
f(t)==
0 Si 0 ≤ t
1 Si t ≥ 0
y
Graficando esta función tenemos:
1
x
Calculando la transforrmada de Laplaace de esta fun
nción:
F [u(t)]=
;
,
Evaluan
ndo en los intervalos de integgración tenemos:
L [u(t)]=
4
Análisis de Sistemas y Señales: Transforrmadas de Laplaace, Z y Fourier.
ƒ Exponencial [Decreciente y creciente]
La función exponencial tiene como función a la sigguiente ecuación:
ndo la transforrmada de Laplaace para la función creciente que tiene valo
ores a>0
*CRECIENTE: Calculan
;
L=
0
S
Sustituimos
la función en la ecuación
e
de la transformada con el intervallo
dado dee 0 a infinito y procedemos a integrar esta función
L=
V
Vemos
que por
p leyes de los exponentees se puede factorizar de la
siguientte manera hacciendo una sum
ma de la potenccia a la que esttán.
L=
C
Como
tenemoss una integral impropia
i
realizzamos el límitee para saber a
qué valor tiende.
L=
Resolviendo
o esto vemos que
q su valor es a cero y ahora sustituimoss su
valor y valuamos la fu
unción teniendo ese resultado.
L=
Esta es la transfo
ormada de Laplace de la funcción exponenccial creciente
5
Análisis de Sistemas y Señales: Transforrmadas de Laplaace, Z y Fourier.
*DECREECIENTE:
;
0
Calculando la transfo
ormada de Laplace para la función decreeciente que tiene valores a<0
a pero que se
ue significa qu
ue la función decaerá.
d
Realizzando los mism
mos pasos quee la
identifica ahora con un signo (‐) qu
or pero tomand
do ahora en cu
uenta el signo tenemos
t
que su transformad
da se calcula dee la
transformada anterio
siguientte manera:
L=
S
Sustituimos
la función en la ecuación
e
de la transformada con el intervallo
dado dee 0 a infinito y procedemos a integrar esta función
L=
V
Vemos
que por
p leyes de los exponentees se puede factorizar de la
siguientte manera hacciendo una sum
ma de la potenccia a la que esttán.
L=
C
Como
tenemoss una integral impropia
i
realizzamos el límitee para saber a
qué valor tiende.
L=
Resolviendo
o esto vemos que
q su valor es a cero y ahora sustituimoss su
valor y valuamos la fu
unción teniendo ese resultado.
L=
ƒ
Esta es la transfo
ormada de Laplace de la funcción exponenccial decreciente
e
Senoidal
X(t) = Acos
A
(ωot+Φ))
Sustituyeendo en la eccuación de la transformada
t
a de Laplace
L =x(s))=
ωot
L =x(s)) =
ωot cos Φ
L =x(s)) =
cos Φ
Φ
Por identidad trigonom
métrica hacem
mos lo siguien
nte:
ωot
PARTE 1
ωot
Φ
Resolviendo la integrall:
Φ
ωot
PA
ARTE 2
6
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
Se ve que la integral completa mejor la dividiéremos en partes y se resolverá cada una.
Resolviendo la parte 1
L =x(s) =
ωot
o
L =x(s) =
ωot
o
L =x(s) = 1
2
o
0
o2 s²
ωot
o²
=
o
=
o2
=
2
o
o2 S²
ωot
o²
o²
ωot
cos ωot)
o2
ωot
o2
s²
=
ωot
o2
2
cos ωot
L =x(s) =
ωot
o²
²
cos ωot
o2
²
ωot
o
ωot
L =x(s) =
L =x(s) =
ωot
o
cos ωot
o2
…. (Parte 1)
Resolviendo la parte 2
L =x(s) =
L =x(s) =
o2
cos ωot
2
o
o2
o2
ωot
sen ωot
o2
sen ωot
o2
o2 s²
cos ωot
o2
ωot
o2
L =x(s) = 1
L =x(s) =
ωot
o2
ωot
cos ωot =
o2
o2
2
o
o2 s²
0
cos ωot)
o
=
o
o2 S²
…. (Parte 2)
Uniendo la parte 1 con la parte 2
L =x(s) = A cos Φ
ωo2 S2
sen Φ
ωo
ωo2 S²
Finalmente tenemos que la transformada de Laplace de esta función es:
L =x(s)
ωot
Φ
=
cos Φ
sen Φ ωo
s² ωo2
7
Análisis de Sistemas y Señales: Transforrmadas de Laplaace, Z y Fourier.
ƒ
Rampa
La función rampa es la integral de laa función escalón. Si considerramos que estamos sumando
o toda el área
bajo la función escaló
ón a hasta un tiiempo t. Si t < 0 (cero), el valor de la integral será 0 (cero). Si es mayor
que 0 (ccero), entonce
es el valor será igual a la integgral de 1 desdee el tiempo 0 hasta
h
el tiempo
o t, la cual
también tiene el valor t, es decir:
G
Gráficamente
te
enemos:
ormada de Lapllace de esta función tenemoss
Calculando la Transfo
F[s] = L [r(t)] =
lim
Realizando la integral por el método
o de por partess (uv‐
u= t
) teenemos:
dv=e‐stdt
du=dt v= ‐ e‐st
F[s] = L [r(t)]= lim
l
; 0, ∞
F[s] = L [r(t)]=
Esta es la Traansformada de
e la Laplace de la Función Rampa
8
Análisis de Sistemas y Señales: Transforrmadas de Laplaace, Z y Fourier.
Transform
mada de Fourier
la transsformada de Fourier
F
es una aplicación que hace corresponder a una función f con valores reales o
compleejos y definida en la recta, otrra función g deefinida de la manera siguientte:
Donde f es L1, o sea f tiene que ser una función in
ntegrable en el sentido de la integral de Leb
besgue. El facttor,
que aco
ompaña la inttegral en defin
nición facilita el enunciado de algunos dee los teoremas referentes a la
transformada de Fo
ourier. Aunquee esta forma de normalizar la transforrmada de Fourier es la más
m
comúnm
mente adoptad
da, no es univeersal.
La transsformada de Fourier así defin
nida goza de una serie de pro
opiedades de continuidad
c
qu
ue garantizan que
q
puede extenderse
e
a espacios
e
de fun
nciones mayorees e incluso a espacios
e
de fun
nciones generaalizadas.
La transsformada de Fourier, tiene una
u multitud dee aplicaciones en muchas áreeas de la cienccia e ingeniería: la
física, laa teoría de los números, la combinatoria, el
e procesamien
nto de señales,, la teoría de laa probabilidad, la
estadísttica, la óptica, la propagació
ón de ondas y otras áreas. En procesamien
nto de señaless la transformaada
de Fou
urier suele con
nsiderarse com
mo la descom
mposición de una señal en componentess de frecuenccias
diferentes, es decir, g corresponde al espectro de frecuencias dee la señal f.
d Fourier teneemos:
Dando una definición formal de la transformada de
Sea f un
na función Lebesgue integrab
ble:
o
La transsformada de Fourier de f es la función es:
ƒ
Pulso
∞
1
2
−∞
∞
−
1
2
0
F (π (t )) = ∫ π (t )e − jωt dt
d = ∫ π (t )e − jωt dt = ∫ π (t )e − jωt dt + ∫ π (t )e − jωt dt
1
2
−
1
2
0
Como es causal:
1
2
1
2
0
0
F (π (t )) = ∫ π (t )e − jωt dt = ∫ (1)e − jωt dt =
1
− jω t 2
− jω
2
e
e
1
=−
+
− jω 0
jω
jω
− jω
⎞
1 ⎛
2
−
F (π (t )) =
1
e
⎟
⎜
jω ⎝
⎠
9
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
ƒ
Impulso
∞
Usando la propiedad:
∫ ∂(t − t ) f (t ) = f (t )
0
0
−∞
ƒ
Escalón
,
,
0
0
Para determinar la Trasformada de Fourier, de cualquier función se sustituye dicha función en la expresión
de la Transformada de Fourier (este va a hacer el proceder en todas las funciones que ejemplificaremos),
como se observa; y se desarrolla la integral impropia recordando de cálculo integral como se resuelven este
tipo de integrales, entonces:
F [u(t)]=
;
,
Evaluando en los intervalos de integración tenemos:
F [u(t)]=
Esta es la Transformada de Fourier para la Función escalón (unitario)
ƒ
Exponencial [Decreciente y creciente]
CRECIENTE
Está definida como: x(t) = eat ; a>0;
Sustituimos en la expresión de Fourier y desarrollamos la integral.
F [x(t)]=
;
,
Evaluando en los intervalos de integración tenemos:
F [x(t)] =
10
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
Esta es la Transformada de Fourier para la Función exponencial creciente
DECRECIENTE
Está definida como: x(t) = e‐at ; a<0;
Sustituimos en la expresión de Fourier y desarrollamos la integral.
F [x(t)]=
;
,
Evaluando en los intervalos de integración tenemos:
F [x(t)] =
Esta es la Transformada de Fourier para la Función exponencial decreciente
ƒ
Senoidal
Transformada de Fourier Senoidal
X(t) = Acos (ωot+Φ)
Sustituyendo en la ecuación de la transformada de Laplace
F =x(f)=
ωot
F =x(f) =
ωot cos Φ
Φ
Por identidad trigonométrica hacemos lo siguiente:
Φ
Resolviendo la integral:
Φ
ωot
ωot
cos Φ
F =x(f) =
ωot
PARTE 1
PARTE 2
Se ve que la integral completa mejor la dividiéremos en partes y se resolverá cada una.
Resolviendo la parte 1
F=x(f) =
F =x(f) =
ωot
o
o
ωot
ωot
o
o
ωot
²
o²
ωot
11
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
²
ωot
F =x(f) =
F =x(f) = 1
cos ωot
o2
2
o
F =x(f) =
0
o2 jw²
=
o
=
=
o2
2
o
o2 jw²
s²
=
ωot
o2
ωot
o²
ωot
o2
2
cos ωot
F =x(f) =
ωot
o²
o²
ωot
cos ωot)
o2
cos ωot
o2
…. (Parte 1)
Resolviendo la parte 2
F =x(f) =
F =x(f) =
2
o
s²
o2
cos ωot
sen ωot
o2
o
2
cos ωot
o2
ωot
o2
F =x(f) = 1
F =x(f =
ωot
o2
2
o
ωot
o2
ωot
sen ωot
o2
cos ωot =
2
o
cos ωot)
o2
2
o
2
o
jw²
0
o
=
o
o2 jw²
…. (Parte 2)
Uniendo la parte 1 con la parte 2
F =x(f) = A cos Φ
ωo2 jw2
sen Φ
ωo
ωo2 jw²
Finalmente tenemos que la transformada de Fourier de esta función es:
F =x(f)
ωot
Φ
=
cos Φ
sen Φ ωo
jw ² ωo2
12
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
ƒ
Rampa
lim
F [r(t)] =
Realizando la integral por el método de por partes (uv‐
u= t
) tenemos:
dv=e‐jwt dt
du=dt v= ‐
e‐jwt
F [r(t)]= lim
; 0, ∞
F [r(t)]=
Esta es la Transformada de la Fourier de la Función Rampa
13
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
Transformada Z
Definición
Sea x(t) una función discreta, definida para t>0. Si se admite un muestreo uniforme con período T de la
función x(t), entonces la señal muestreada en t=kT (k=0,1,...), la representaremos por x(kT). La transformada
z de x(t), o de la secuencia de valores x(kt), se define como:
Análogamente, la transformada z de una secuencia de números x(k), se define como:
Calculando la transformada Z de las funciones elementales
ƒ
Pulso
La función definida por este pulso unitario esta descrita por la siguiente ecuación: x(t) =
1; t = 0
0; t ≠ 0
Aplicando la ecuación (2) para esta ecuación vemos que tenemos el siguiente resultado:
0
0
0
0
Vemos que esta serie converge a solo el valor 1 ya que sus demás valores se convierten en 0 dando así como resultado
de la transformada Z de esta ecuación Z =
ƒ
Impulso
Ahora bien, recordemos que en cursos de Cálculo se ve la serie geométrica, y los valores para los cuales
converge esta serie. Se tiene de hecho que:
solo si
Para los demás valores de r, la serie geométrica es divergente. Usando este resultado, podemos concluir
que:
si
Teniendo como resultado:
14
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
ƒ
Escalón
La función escalón unitario se define con la siguiente ecuación:
Aplicando la ecuación (2) su transformada Z es la siguiente:
Estas series son resueltas con las series geométricas teniendo la formula
Utilizando la siguiente expresión
Ubicamos a = 1 y r =
y simplemente sustituimos.
La serie converge a la siguiente expresión que es el resultado de esta transformada Z
ƒ
Exponencial [Decreciente y creciente]
La función exponencial decreciente se define con la siguiente ecuación:
Aplicando la ecuación (2) su transformada Z es la siguiente:
Utilizando la siguiente expresión
sustituimos.
Ubicamos a = 1 y r =
y simplemente
La serie converge a la siguiente expresión que es el resultado de esta transformada Z
La función exponencial creciente se define con la siguiente ecuación pero ahora con los valores para a positivos:
Utilizando la siguiente expresión
sustituimos.
Ubicamos a = 1 y r =
y simplemente
Aplicando la ecuación (2) su transformada Z es la siguiente:
La serie converge a la siguiente expresión que es el resultado de esta transformada Z
15
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
ƒ
Senoidal
A cos(ωt + φ ) = A[ cos(ωt ) cos(φ ) − sin(ωt )sin(φ )]
para la transformada z:
y(t)=
A cos(ωt + φ )
y(kt)=
A cos(ω kt + φ ) =
A [ cos(ω kt ) cos(φ ) − sin(ω kt )sin(φ )]
y(z)=
∞
∑ y(kt ) z
k =0
−k
∞
= ∑ A [ cos(ω kt ) cos(φ ) − sin(ω kt ) sin(φ ) ]z − k
k =0
∞
∞
= A cos(φ )∑ cos(ω kt )z − k − A sin(φ )∑ sin(ω kt )z − k
k =0
k =0
⎡cos(φ ) {1 + cos(ωt ) z + cos(2ωt ) z −2 + cos(3ωt ) z −3 }⎤
⎥
= A⎢
⎢ − sin(φ ) {sin(ωt ) z −1 + sin(2ωt ) z −2 + sin(3ωt ) z −3 } ⎥
⎣
⎦
−1
se sabe que: cos( wt ) = (−1) w
⎡ cos(φ ) {1 + (−1) w z −1 + (−1) 2 w z −2 + (−1)3 w z −3 }
⎤
⎥
y(z)= = A ⎢
⎢ − sin(φ ) {sin(ωt ) z −1 + sin(2ωt ) z −2 + sin(3ωt ) z −3 }⎥
⎣
⎦
{
}
{
}
kw − k
− sin(φ ) sin(kωt ) z − k ⎤⎦ k = 1, 2, 3, 4,.........
y(z)= = A ⎡⎣cos(φ ) (−1) z
en donde: A es amplitud, ω es frecuencia , φ es ángulo de fase.
16
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
ƒ
Rampa
La función rampa unitaria se define con la siguiente ecuación:
Aplicando la ecuación (2) su transformada Z es la siguiente:
Utilizando la siguiente expresión
sustituimos.
Ubicamos a = T
y r=
y simplemente
La serie converge a la siguiente expresión que es el resultado de esta transformada Z
17
Análisis de Sistemas y Señales: Transformadas de Laplace, Z y Fourier.
BIBLIOGRAFÍA
¾ Kemen, Edward, Introducción a Señales y sistemas
¾ Oppenheim Alan, Señales y Sistemas
18