UNIDADES TECNOLOGICAS DE SANTANDER
DEPARTAMENTO DE CIENCIAS BASICAS
PRIMER PARCIAL DE CÁLCULO MULTIVARIABLE
♦
PRUEBA ESCRITA (60 % de la nota del corte)
Nombre:
Código:
Programa:
Grupo:
Resultado:
Fecha:
Profesor: FABIÁN ANDRÉS
GONZÁLEZ C.
Ítem
RESULTADOS DE APRENDIZAJE
Identificar el dominio, imagen y grafica de superficies de tres dimensiones a partir de su expresión algebraica.
1-4
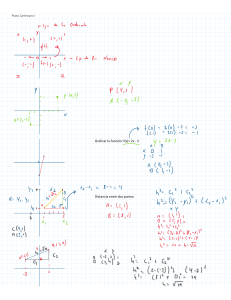
1. (1 punto) La trayectoria de un planeta alrededor de una estrella es elíptica, tal que cumple con las leyes descritas
por Johannes Keppler. Tomando en cuenta que el centro de la elipse corresponde al origen de coordenadas y uno de
sus vértices, se encuentra en la posición (0,8), calcule la excentricidad de la elipse (0,3 puntos), escriba la ecuación
de la trayectoria (0,4 puntos) y realice el dibujo en el plano cartesiano (0,3 puntos), suponiendo, que la posición
focal donde se encuentra la estrella, es (0,6)
La elipse tiene centro en (0,0)
La longitud del semieje menor, puede ser calculada utilizando la relación con la
distancia focal
2
𝑠𝑒𝑚𝑖𝑒𝑗𝑒 √ 𝑠𝑒𝑚𝑖𝑒𝑗𝑒
𝑠𝑒𝑚𝑖𝑒𝑗𝑒
= (
) − 𝑐 2 = √82 − 62 ⇒
≈ 5.3
𝑚𝑎𝑦𝑜𝑟
𝑚𝑒𝑛𝑜𝑟
𝑚𝑒𝑛𝑜𝑟
La ecuación de la elipse es
1
𝑥2 𝑦2
+
=1
28 64
Una vez obtenido este resultado, se puede determinar la excentricidad
𝑒=
2. La función −
𝑧2
4
−
𝑥2
4
6
= 0.75
8
= 𝑦 describe un paraboloide elíptico en el espacio tridimensional. Escriba la ecuación de las
trazas para los siguientes valores de z y dibuje las curvas de nivel.
Plano de la
traza para
Función de la traza (0.3 puntos c/u)
𝑧2 9
9
− = 𝑦 ⇒ 𝑧 2 = −4 (𝑦 + )
4 4
4
x=3
−
y = -5
−
z = -4
−
Gráfica de la traza en z = -4 (0.5 puntos)
𝑧2 𝑥2
𝑧2 𝑥2
−
= −5 ⇒
+
=1
4
4
20 20
16 𝑥 2
−
= 𝑦 ⇒ 𝑥 2 = −4 (𝑦 + 4)
4
4
“Ni siquiera la propia naturaleza sabe que camino va a seguir el electrón.” – R. Feynman
UNIDADES TECNOLOGICAS DE SANTANDER
DEPARTAMENTO DE CIENCIAS BASICAS
PRIMER PARCIAL DE CÁLCULO MULTIVARIABLE
♦
3. Determine la posición del foco (0.3 puntos) y la ecuación de la directriz de la parábola (0.3 puntos) descrita por la
función (𝑥 − 4)2 = 12(𝑦 − 3). Realice el dibujo en el plano cartesiano (0.5 puntos).
Solución: A partir de la ecuación, se puede determinar
fácilmente que el vértice está en la posición (4,3) y el valor de p
= 3. Una vez obtenido este resultado, y con ayuda de la gráfica,
se puede determinar fácilmente, que el foco está en la posición
(4,6) y la directriz la ecuación 𝑦 = 0.
4
4. El cambio de precios en una empresa multinacional, depende de las variables 𝑥 y 𝑦, que están relacionadas con la
fluctuación de los mercados a nivel internacional de la forma 𝑧 = 𝐿𝑛(𝑥𝑦 − 1) + 𝑦 2 . Determine el dominio de la
función, de tal manera que exista la función (0.5 puntos) y grafique su resultado en el plano cartesiano (1 punto).
Solución: Debido a que el dominio de 𝑦 2 es el conjunto de los reales, se establece que el logaritmo natural es quien
restringe el conjunto de valores que pueden tomar las variables 𝑥 y 𝑦, por lo que se establece la condición para el
argumento del logaritmo
𝑥𝑦 − 1 > 0
1
De esta expresión se determina que los valores del dominio son aquellos que cumplen la condición son 𝑦 > 𝑥, de tal
manera, que este puede ser escrito de la siguiente manera:
1
𝐷: {(𝑥, 𝑦)| 𝑦 > }
𝑥
Y su representación en el plano es la región señalada en color verde
“Ni siquiera la propia naturaleza sabe que camino va a seguir el electrón.” – R. Feynman
2
UNIDADES TECNOLOGICAS DE SANTANDER
DEPARTAMENTO DE CIENCIAS BASICAS
PRIMER PARCIAL DE CÁLCULO MULTIVARIABLE
♣
PRUEBA ESCRITA (60 % de la nota del corte)
Nombre:
Código:
Programa:
Grupo:
Resultado:
Fecha:
Profesor: FABIÁN ANDRÉS
GONZÁLEZ C.
Ítem
RESULTADOS DE APRENDIZAJE
Identificar el dominio, imagen y grafica de superficies de tres dimensiones a partir de su expresión algebraica.
1-4
1. (1 punto) La trayectoria de un planeta alrededor de una estrella es elíptica, tal que cumple con las leyes descritas
por Johannes Keppler. Tomando en cuenta que el centro de la elipse corresponde al origen de coordenadas y uno de
sus vértices, se encuentra en la posición (0,8), calcule la excentricidad de la elipse (0,3 puntos), escriba la ecuación
de la trayectoria (0,4 puntos) y realice el dibujo en el plano cartesiano (0,3 puntos), suponiendo, que la posición
focal donde se encuentra la estrella, es (0,6)
La elipse tiene centro en (0,0)
La longitud del semieje menor, puede ser calculada utilizando la relación con la
distancia focal
2
𝑠𝑒𝑚𝑖𝑒𝑗𝑒 √ 𝑠𝑒𝑚𝑖𝑒𝑗𝑒
𝑠𝑒𝑚𝑖𝑒𝑗𝑒
= (
) − 𝑐 2 = √82 − 62 ⇒
≈ 5.3
𝑚𝑎𝑦𝑜𝑟
𝑚𝑒𝑛𝑜𝑟
𝑚𝑒𝑛𝑜𝑟
La ecuación de la elipse es
3
𝑥2 𝑦2
+
=1
28 64
Una vez obtenido este resultado, se puede determinar la excentricidad
𝑒=
2. La función −
𝑧2
5
−
𝑦2
5
6
= 0.75
8
= 𝑥 describe un paraboloide elíptico en el espacio tridimensional. Escriba la ecuación de la
traza para los siguientes valores de z y dibuje las curvas de nivel.
Plano de la
traza para
Función de la traza (0.3 puntos c/u)
Gráfica de la traza en y = -1 (0.5 puntos)
𝑧2 𝑦 2
𝑧2 𝑦 2
−
= −6 ⇒
+
=1
5
5
30 30
x = -6
−
y = -1
−
z=3
9 𝑦2
9
− −
= 𝑥 ⇒ 𝑦 2 = −5 (𝑥 + )
5 5
5
𝑧2 1
1
− = 𝑥 ⇒ 𝑧 2 = −5 (𝑥 + )
5 5
5
“Ni siquiera la propia naturaleza sabe que camino va a seguir el electrón.” – R. Feynman
UNIDADES TECNOLOGICAS DE SANTANDER
DEPARTAMENTO DE CIENCIAS BASICAS
PRIMER PARCIAL DE CÁLCULO MULTIVARIABLE
♣
3. Determine la posición del foco (0.3 puntos) y la ecuación de la directriz de la parábola (0.3 puntos) descrita por la
función (𝑥 − 4)2 = 12(𝑦 − 3). Realice el dibujo en el plano cartesiano (0.5 puntos).
Solución: A partir de la ecuación, se puede determinar
fácilmente que el vértice está en la posición (4,3) y el valor de p
= 3. Una vez obtenido este resultado, y con ayuda de la gráfica,
se puede determinar fácilmente, que el foco está en la posición
(4,6) y la directriz la ecuación 𝑦 = 0.
4
4. El cambio de precios en una empresa multinacional, depende de las variables 𝑥 y 𝑦, que están relacionadas con la
fluctuación de los mercados a nivel internacional de la forma 𝑧 = 𝐿𝑛(1 − 𝑥𝑦) + 𝑥 2 . Determine el dominio de la
función, de tal manera que exista la función (0.5 puntos) y grafique su resultado en el plano cartesiano (1 punto).
Solución: Debido a que el dominio de 𝑦 2 es el conjunto de los reales, se establece que el logaritmo natural es quien
restringe el conjunto de valores que pueden tomar las variables 𝑥 y 𝑦, por lo que se establece la condición para el
argumento del logaritmo
1 − 𝑥𝑦 > 0
1
De esta expresión se determina que los valores del dominio son aquellos que cumplen la condición son 𝑦 < 𝑥 , de
tal manera, que este puede ser escrito de la siguiente manera:
1
𝐷: {(𝑥, 𝑦)| 𝑦 < }
𝑥
Y su representación en el plano es la región señalada en color verde
“Ni siquiera la propia naturaleza sabe que camino va a seguir el electrón.” – R. Feynman
4