ALGEBRA DE MATRICES (1)

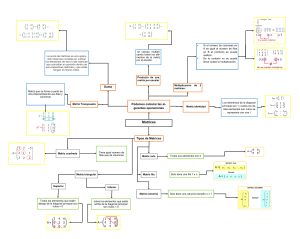
ALGEBRA DE MATRICES
MATRICES
Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester
El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853
En 1858, A. Cayley introduce la notación matricial como una forma abreviada de
escribir un sistema de m ecuaciones lineales con n incógnitas.
Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de
ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
Además de su utilidad para el estudio de sistemas de ecuaciones lineales, las matrices
aparecen de forma natural en geometría, estadística, economía, informática, física, etc.
La utilización de matrices (arrays) constituye actualmente una parte esencial dn los
lenguajes de programación, ya que la mayoría de los datos se introducen en los
ordenadores como tablas organizadas en filas y columnas: hojas de cálculo, bases de
datos,...
CONCEPTO DE MATRIZ
Una matriz es un conjunto de elementos de cualquier naturaleza aunque, en general,
suelen ser números ordenados en filas y columnas.
Se llama matriz de orden "m × n" a un conjunto rectangular de elementos aij
dispuestos en m filas y en n columnas. El orden de una matriz también se denomina
dimensión o tamaño, siendo m y n números naturales.
Las matrices se denotan con letras mayúsculas: A, B, C, ... y los elementos de las
mismas con letras minúsculas y subíndices que indican el lugar ocupado: a, b, c, ... Un
elemento genérico que ocupe la fila i y la columna j se escribe aij . Si el elemento
genérico aparece entre paréntesis también representa a toda la matriz : A = (aij)
Cuando nos referimos indistíntamente a filas o columnas hablamos de lineas.
El número total de elementos de una matriz Am×n es m·n
En matemáticas, tanto las Listas como las Tablas reciben el nombre genérico de
matrices.
Una lista numérica es un conjunto de números dispuestos uno a continuación del otro.

MATRICES IGUALES
Dos matrices A = (aij)m×n y B = (bij)p×q son iguales, sí y solo si, tienen en los
mismo lugares elementos iguales, es decir :

ALGUNOS TIPOS DE MATRICES
Hay algunas matrices que aparecen frecuentemente y que según su forma, sus
elementos, ... reciben nombres diferentes :
Tipo de matriz
FILA
Definición
Aquella matriz que tiene una
sola fila, siendo su
orden 1×n
COLUMNA
RECTANGULAR
Aquella matriz que tiene una
sola columna, siendo su
orden m×1
Aquella matriz que tiene
distinto número de filas que
de columnas, siendo su
orden m×n ,
TRASPUESTA
Dada una matriz A, se
llama traspuesta de A a la
matriz que se obtiene
cambiando ordenadamente
las filas por las columnas.
Se representa por At ó AT
OPUESTA
La matriz opuesta de una
dada es la que resulta de
sustituir cada elemento por
su opuesto. La opuesta de
A es -A.
NULA
Si todos sus elementos
son cero. También se
denomina matriz cero y
se denota por 0m×n
CUADRADA
Aquella matriz que
tiene igual número de
filas que de columnas,
m = n, diciendose que
Ejemplo
la matriz es de orden n.
Diagonal principal : son
los elementos a11 , a22 ,
...,
ann
Diagonal secundaria :
son los elementos aij
con
i+j = n+1
Traza de una matriz
cuadrada : es la suma
de los elementos de la
diagonal principal tr A.
SIMÉTRICA
Es una matriz cuadrada
que es igual a su
traspuesta.
A = At , aij = aji
ANTISIMÉTRICA
Es una matriz cuadrada
que es igual a la
opuesta
de
su
traspuesta.
A = -At , aij = -aji
Necesariamente aii =
0
DIAGONAL
Es una matriz cuadrada
que tiene todos sus
elementos nulos excepto
los de la diagonal
principal
ESCALAR
Es una matriz cuadrada
que tiene todos sus
elementos nulos excepto
los de la diagonal
principal
que
son
iguales
IDENTIDAD
Es una matriz cuadrada
que tiene todos sus
elementos nulos excepto
los de la diagonal
principal
que
son
iguales a 1. Tambien se
denomina
matriz
unidad.
Diagonal
principal
:
Diagonal
secundaria
:
TRIANGULAR
Es una matriz cuadrada
que tiene todos los
elementos por encima
(por debajo) de la
diagonal
principal
nulos.
Una matriz ortogonal
es
necesariamente
cuadrada e invertible :
A-1
=
AT
ORTOGONAL
La inversa de una matriz
ortogonal es una matriz
ortogonal.
El producto de dos matrices
ortogonales es una matriz
ortogonal.
El determinante de una
matriz ortogonal vale +1 ó 1.
NORMAL
Una matriz es normal si
conmuta
con
su
traspuesta.
Las
matrices
simétricas,
antisimétricas
u
ortogonales
son
necesariamente
normales.
INVERSA
Decimos que una matriz
cuadrada A
tiene
inversa, A-1, si se
verifica
que
:
-1
-1
A·A = A ·A = I
Para establecer las reglas que rigen el cálculo con matrices se desarrolla un álgebra
semejante al álgebra ordinaria, pero en lugar de operar con números lo hacemos con
matrices.
Explicaciones generales
matriz 3 x 4
fila
columna
El primer número nos indica el número de filas que tiene la matriz.
El segundo indica la cantidad de columnas que tiene la matriz.
Ejemplo:
3 filas
1 2 3 4 
5 6 7 8 


9 10 11 12




La matriz es 3 x 4
4 columnas
Si la matriz es A las posiciones de cada número son aij
i es la fila y j es la columna donde se encuentra posicionado el número en la matriz
A.
Si la matriz es B las posiciones de cada número son bij
i es la fila y j es la columna donde se encuentra posicionado el número en la matriz
B.
Ejemplos:
 a11 a12
A  a21 a22
a31 a32
a13 
a23 
a33 
b11 b12 b13 
B  b21 b22 b23 
b31 b32 b33 
En la siguiente matriz indica la posición del número circulado.
1 2 3 4
5 6 7 8

A
 9 10 11 12


13 14 15 16
2 __________
7 __________
9 __________
14 __________
Suma de matrices
Para poder sumar matrices deben de tener el mismo orden, ambas matrices deben
tener el mismo número de filas y columnas.
Definición de suma:
Si A = (aij) m x n y B = (bi j) m x n entonces su suma es A + B = (aij + bij) m x n.
Ejemplo:
1+5=6
Suma las matrices A + B
A
1 3
5 7
B
5 7
4 8
1 3 5 7 6


5 7 4 8
Suma a1 1
+
b1 1
3 + 7 = 10
1 3 5 7 6 10


5 7 4 8
1 3 5 7 6 10


5 7 4 8 9
Suma a1 2
+
b1 2
Suma a2 1
+
b2 1
Suma a2 2
+
b2 2
5+4=9
1 3 5 7 6 10


5 7 4 8 9 15
7 + 8 = 15
Propiedades:
Ley asociativa
Ley conmutativa
A  B  C    A  B   C
A B  B  A
Elemento neutro
0 0 1 2 1 2


0 0 3 4 3 4
Producto de un escalar
Definición:
Si kA = k(ai j) mxn
Debes multiplicar cada número de la matriz por el escalar.
Ejemplo:
Opera 2A
A
1 5
3 4
2A  2
1 5 2 10

3 4 6 8
Inverso aditivo (resta)
A
2 3
4 1
B
4 5
1 2
Opera A – B
A B 
2 3  4 5 6 8


4 1 1 2 5  3
El orden es igual que en la suma pero debes
fijarte muy bien en los signos.
Multiplicación de matrices:
Para poder multiplicar debemos revisar primero el numero de filas x columnas
Si tenemos que una matriz es 3 x 5
Matriz A
y la otra 5 x 2 se puede multiplicar si
Matriz B
El tamaño de la
respuesta es 3 x 2
3 x 5
5 x 2
Si los números centrales son
iguales entonces se puede
multiplicar y el tamaño de la
respuesta son los números de los
extremos 3 x 2
Debe ser igual entonces
si se puede multiplicar
Resuelve el siguiente ejercicio e indica si se puede multiplicar las matrices o no, y cual es el tamaño
de la matriz de la respuesta.
Matriz A
Matriz B
3x4
5x6
5x3
7x8
4x2
5x7
3x1
4x3
2x5
¿se puede multiplicar?
Tamaño de respuesta
4x5
6x2
4x6
8x2
3x4
7x2
1x4
4x3
5x4
Ejemplo:
0 1 2

3 4 5
6 7 8
33
9 10 11  
12 13 14 



1) Reviso el tamaño de la matriz
A= 2x3 B=3x3
Como son iguales se puede
multiplicar.
El tamaño de la matriz de la
respuesta es 2 x 3
Se opera así:
0  6  1 9  2 12 
0  9  24  33
2)
Siempre se toma la primera matriz
con la fila 1 (horizontal) con la 1
columna (vertical) marcada en la
matriz.
0 1 2

3 4 5
6 7 8
33 36
9 10 11  
12 13 14 



0  7  110  2 13 
0  10  26  36
0 1 2

3 4 5
6 7 8
33 36 39
9 10 11  


12 13 14 
0  8  111  2 14 
0  11  28  39
0 1 2

3 4 5
6 7 8
 33 36 39
9 10 11  

114


12 13 14
3  6  4  9  5  12 
18  36  60  114
0 1 2

3 4 5
6 7 8
 33 36 39
9 10 11  

114 126

12 13 14 
3  7  4  10  5  13 
21  40  65  126
0 1 2

3 4 5
6 7 8
 33 36 39 
9 10 11  
114 126 138

12 13 14
3  8  4  11  5  14 
24  44  70  138
Respuesta:
0 1 2

3 4 5
6 7 8
33 36 39
9 10 11 
114 126 138
12 13 14