pdf-problema-desarroladas compress

PROBLEMA 11.
En el área de SMT. Se busca reducir los defectos ocasionados por impresiones de
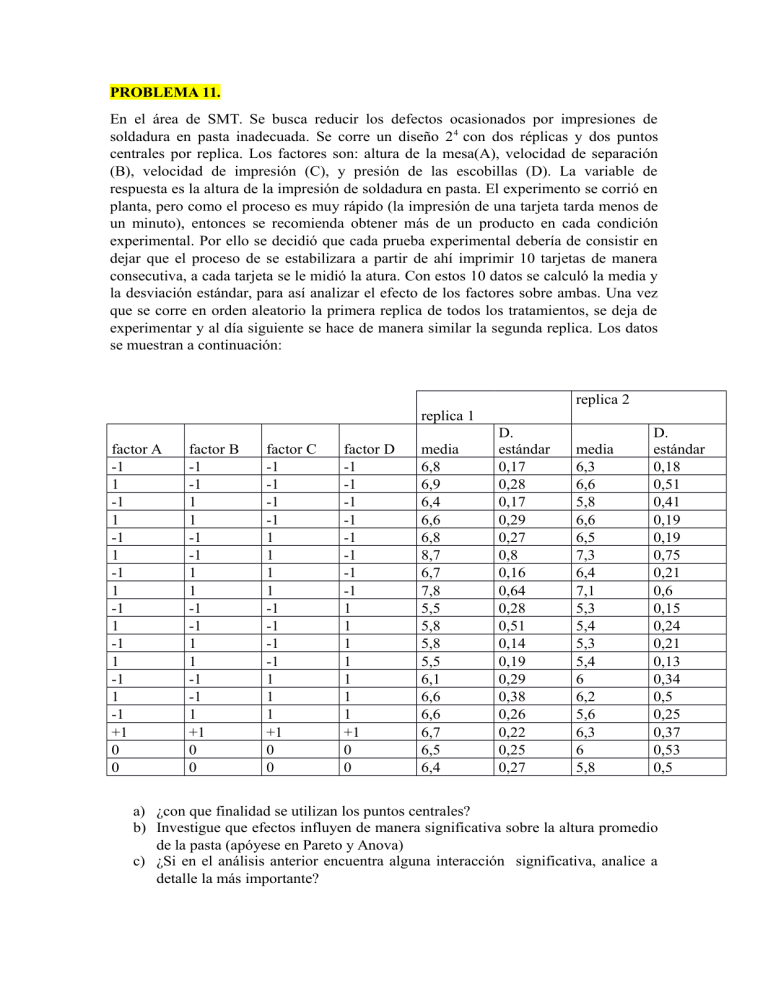
soldadura en pasta inadecuada. Se corre un diseño 2 4 con dos réplicas y dos puntos
centrales por replica. Los factores son: altura de la mesa(A), velocidad de separación
(B), velocidad de impresión (C), y presión de las escobillas (D). La variable de
respuesta es la altura de la impresión de soldadura en pasta. El experimento se corrió en
planta, pero como el proceso es muy rápido (la impresión de una tarjeta tarda menos de
un minuto), entonces se recomienda obtener más de un producto en cada condición
experimental. Por ello se decidió que cada prueba experimental debería de consistir en
dejar que el proceso de se estabilizara a partir de ahí imprimir 10 tarjetas de manera
consecutiva, a cada tarjeta se le midió la atura. Con estos 10 datos se calculó la media y
la desviación estándar, para así analizar el efecto de los factores sobre ambas. Una vez
que se corre en orden aleatorio la primera replica de todos los tratamientos, se deja de
experimentar y al día siguiente se hace de manera similar la segunda replica. Los datos
se muestran a continuación:
replica 2
replica 1
factor A
-1
1
-1
1
-1
1
-1
1
-1
1
-1
1
-1
1
-1
+1
0
0
factor B
-1
-1
1
1
-1
-1
1
1
-1
-1
1
1
-1
-1
1
+1
0
0
factor C
-1
-1
-1
-1
1
1
1
1
-1
-1
-1
-1
1
1
1
+1
0
0
factor D
-1
-1
-1
-1
-1
-1
-1
-1
1
1
1
1
1
1
1
+1
0
0
media
6,8
6,9
6,4
6,6
6,8
8,7
6,7
7,8
5,5
5,8
5,8
5,5
6,1
6,6
6,6
6,7
6,5
6,4
D.
estándar
0,17
0,28
0,17
0,29
0,27
0,8
0,16
0,64
0,28
0,51
0,14
0,19
0,29
0,38
0,26
0,22
0,25
0,27
media
6,3
6,6
5,8
6,6
6,5
7,3
6,4
7,1
5,3
5,4
5,3
5,4
6
6,2
5,6
6,3
6
5,8
D.
estándar
0,18
0,51
0,41
0,19
0,19
0,75
0,21
0,6
0,15
0,24
0,21
0,13
0,34
0,5
0,25
0,37
0,53
0,5
a) ¿con que finalidad se utilizan los puntos centrales?
b) Investigue que efectos influyen de manera significativa sobre la altura promedio
de la pasta (apóyese en Pareto y Anova)
c) ¿Si en el análisis anterior encuentra alguna interacción significativa, analice a
detalle la más importante?
d) Si se quiere un valor de 6.0 para la altura de la pasta, ¿Cuáles son las
condiciones para lograrlo?
e) Ahora investigue que efectos influyen de manera relevante sobre la variabilidad
de la altura de la pasta.
f) Encuentre una condición satisfactoria tanto para la altura como para minimizar
la variabilidad.
g) De los análisis de varianza para la media y desviación estándar vea el coeficiente
R2 ¿que concluye de ello?
h) ¿Hay evidencia de curvatura?
i) Verifique residuos.
Respuestas de las alternativas
a) La finalidad con la cual se utilizan los puntos centrales es para poder mejorar el
método de análisis para cada proceso nivel y/o tratamiento que se aplicara
durante todo el proceso de análisis, es la calidad e lo modelo que se pueda medir
para asegurar los variables estadísticos esperados.
b) Los efectos que influye de manera significativa sobre el promedio de la pasta
son los siguientes:
Las variables que afectan en la altura son el factor “C” y la interacción “AB”
según la gráfica de Pareto.
Según la Anova el P-Valor en el factor “C” es igual a: 0,0142, por lo tanto se
rechaza la hipótesis nula, por lo tanto afecta en la altura.
c) La interacción más significativa en la altura es “AB”, afecta en la altura con un
P-valor: 0.0372, donde se rechaza la hipótesis nula.
d) Si tenemos valor- p = 6 entonces rechazamos la hipótesis nula para alpha = 0,05.
e) La pendiente para el factor “C” es mayor en relación con los demás para que
estas puedan influir en la respuesta.
f) Si
exclúyenos
el
factor
“C”
se
rechaza la hipótesis
nula. es decir que los demás factores no influyen en la altura.
g) LA calidad del modelo está dentro del rango establecido 70%≤71.48≤100% lo
que indica que nuestro modelo de prueba tenemos que mejorar mas es decir
ajustar más, lo que indica que más dispersión de nuestro datos estadísticos.
h) No hay indicios de mucha dispersión porque poco influye los factores en la
respuesta.
i) Los datos residuales en nuestro experimento es Auto correlación residual
Lag 1 = -0,0923312, lo que indica que en la intersección AB hay más residual la
cual se aproxima a la pendiente inversa.
14.- Una de las variables críticas en el proceso de ensamble del brazo lector de un disco
duro es el ángulo que este forma con el cuerpo principal de la cabeza lectora. Se corre
un experimento con el objetivo de comparar dos equipos que miden dicho ángulo en
unidades de radianes. Se decide utilizar como factor de bloque a los operadores de los
equipos. Los resultados se muestran en la siguiente tabla:
a)
b)
c)
d)
Plantee el modelo y las hipótesis más adecuadas del problema.
¿Existen diferencias entre los equipos? Argumente estadísticamente.
¿Existen diferencias entre los operadores?
Dibuje os diagramas de cajas simultaneas y las gráficas de medias para ambos
factores, después interprételas.
e) Verifique los supuestos de normalidad e igualdad de varianza entre tratamientos
así como la posible presencia de puntos aberrantes.
SOLUCION:
1. Planteamiento.
Ensamble de
brazo lector de
disco duro
1
Operador
2
3
Equipo
1
2
total
1
1.267
7
1.041
0
2.308
7
Equipo
1
2
1.328, 0.985, 1.316, 1.553, 1.310, 1.273, 0.985, 1.134, 1.142, 0.917,
1.113, 1.057, 1.144, 1,485, 1,386. 0.789, 0.671, 0.554, 1.386, 1.289.
1.269, 1.268, 1.091, 1.195, 1,380, 1.036, 0.783, 1.108, 1.129, 1.132
1.093, 0.984, 1.087, 1.482, 1.442. 0.021, 0.900, 0.916, 1.434, 1.223.
1.440, 1.079, 1.389, 1611, 1.445,
1.454, 1.063,1.219, 1.602, 1.583,
1.150, 1.190, 1.247, 1.617, 1.574. 1.018, 1.050, 0.997, 1.538, 1.478.
Operador
2
3
1.229 1.374
1
2
0.986 1.300
2
2
2.215 2.674
3
4
Y1 = 3.871; Y2 = 3.3274; Y3 = 7.1984
SC = (1.26772 + 1.0412 + 1.22912 +
0.98622 + 1.37422 + 1.30022) = 8.75296722
2
SCT = 8.75296722 –
(7.1984 )
6
= 0.116807
SCTRAT =
SC E=
( 3.8712) +(3.3274 2) (7.19842 )
−
3
6
=0.04925
( 2.30872 ) + ( 2.2153 2) +(2.6744 2) (7.19842 )
−
2
6
=0.058872
SC E=0.116807−0.049205−0.058872=0.008684
Fuente de
variación
Equipo
Operador
Error
Total
Suma de
cuadrados
0.04925
0.058872
0.08684
0.116807
Grados de
libertad
1
2
2
5
Cuadrado
medio
0.04925
0.029436
0.004322
F0
Valor-p
11.34
6.78
0.078
0.129
a) Plantee el modelo y las hipótesis más adecuadas al problema.
Modelo estadístico:
Yij =
H 0 : μ 1=μ2=…=μk =μ
H A : μi ≠ μ j para alguni ≠ j
b) ¿existe diferencia entre los equipos’ argumente estadísticamente
No existe diferencia ya que el valor – p en tratamiento equipo es de 0.078 (mayor fue
α ) pr lo tanto se acepta la hipótesis nula, lop dos equipos son
0.05 de
estadísticamente iguales.
c) ¿existe diferencias entre los operadores?
No existe diferencias entre el factor de bloque operadores, valor – p 0.129 > 0.05, son
estadísticamente iguales.
d) Dibuje los diagramas de cajas simultáneos y las gráficas d medias para amos medias y
después interprételas.
e)
8. En una empresa lechera se han tenido problemas con viscosidad
de cierta bebida de chocolate. Se creé que los tres ingredientes que
se agregan en pequeñas cantidades se puede
resolver este
problema por lo que es necesario explorar la situación para ello se
corre un experimento 23 con dos replicas. A continuación se
aprecian los resultados obtenidos.
a) Estime todos los posibles efectos y
significativos: Gráfi co de Pareto estandarizado para viscosidad
diga
C :ingr ed iente C
cuales
+
-
B :ingr ed iente B
BC
AB
A :ingr ed iente A
AC
0
2
4
Efectos estandarizados
6
8
son
 se observa 6 efectos; pero los efectos significativos son solo
dos (ingrediente c y b); mientras que los efectos que están
debajo de la línea no son significativos y por ello se mandan al
error.
b) Realice un análisis de varianza de estos datos y obtenga
conclusiones generales:
Prueba de hipótesis:
Si:
donde: α=0.05
Valor-p<α
Análisis de la Varianza para viscosidad
-------------------------------------------------------------------------------Fuente
Suma de Cuadrados
Gl Cuadrado medio FRatio P-Valor
-------------------------------------------------------------------------------B: ingrediente B
5,64062
1
5,64062
6,99
0,0203
C: ingrediente C
33,3506
1
33,3506
41,32
0,0000
Error Total
10,4931
13
0,807163
-------------------------------------------------------------------------------Total (corr.)
49,4844
15
 de acuerdo a los valores de “p-valor” rechazamos la hipótesis nula; y
aceptamos la hipótesis alternativa; debido a que los valores son
menores que 0,05; entonces decimos de que los ingredientes b y c
son significativos en un 95% en la viscosidad.
c) Interprete a detalle los efectos significativos.
Gráfico de Pareto estandarizado para viscosidad
+
-
C:ingr ediente C
B :ingr ediente B
0
2
4
Efectos estandarizados
6
8
 De acuerdo este grafico se puede observar y decir de que el
ingrediente C y B se alejan de la línea de papel normal y que
es señal de que son efectos reales en el proceso.
Gráfico de Efectos principales para viscosidad
18
viscosidad
17
16
15
14
-1 ,0
1,0
-1 ,0
ingr ed iente B
1,0
ingr ediente C
 De esta grafica; se puede concluir que a mayor cantidad de
ingrediente B mayor viscosidad, a mayor proporción del
ingrediente C también será mayor la viscosidad.
d) ¿hay un tratamiento ganador para minimizar?
 Por lo tanto, el mejor tratamiento o el tratamiento ganador;
para minimizar la viscosidad es utilizando la combinación
“ingrediente B en su nivel bajo y el ingrediente C en su nivel
bajo”.
e) Verifique residuos. ¿Qué considera destacado?
r e s id u o s
Gráfico de residuos para viscosidad
1,5
1
0,5
0
-0,5
-1
-1,5
13
15
17
19
21
pronosticado
 De acuerdo a esta figura podemos afirmar de que los puntos
caen aleatoriamente en el sentido vertical dentro de la banda
horizontal, además cabe destacar que la dispersión más
compacta se encuentra en la segunda columna de puntos en
relación con otras tres. De aquí podemos concluir; de que la
menor dispersión obtenida ocurre justo en el punto donde la
viscosidad es menor.
13. se requiere aumentar el rendimiento de un proceso, y para ello
se estudian tres factores con dos niveles cada uno. Se hacen
repeticiones en cada tratamiento del diseño factorial 23 resultante.
La variable de respuesta que se mide es rendimiento. Los datos
son los siguientes:
Tratamiento
Repeticiones
1
22
32
35
55
44
40
60
39
(1)
A
B
Ab
C
Ac
Bc
Abc
2
31
43
34
47
45
37
50
41
3
25
29
50
46
38
36
54
47
a) ¿Cuáles efectos están activos?
Gráfico de Pareto estandarizado para rendimiento
B:dos
+
-
AC
C:tres
BC
AB
A:uno
0
1
2
3
4
Efectos estandarizados
5
 Los efectos que están activos son aquellos que están por
encima de la línea (B: dos, AC y C: tres); mientras las que se
encuentran debajo de la línea son efectos con diferente
importancia; es decir de que solo; 3 de los efectos tienen los pvalores inferiores a 0,05, indicando que son estadísticamente
significativas diferentes de cero al 95,0% de nivel de confianza.
b) Si obtuvo una interacción importante,
detalle. Gráfico de la interacción para rendimiento
re n d im ie n to
49
interprétela
con
tres=1,0
45
tres=-1,0
tres=1,0
41
37
33
tres=-1,0
-1,0
uno
1,0
 En este grafico se puede ver que hay una interacción de puntos; por
tanto existe los efectos principales.
 Entonces decimos que; cuando uno se incrementa o cambia de (-1) al
(1), cuando tres es igual a (1), el rendimiento decrece de manera
importante; pero si tres es igual a (-1), el rendimiento aumenta. Por
tanto concluyamos de que el mejor rendimiento se obtiene cuando
uno se encuentra en su nivel bajo (-1).
c) Determine las condiciones de operación que maximizan el
rendimiento.
Cabe mencionar; que a mayor factor “dos”
mayor será el
rendimiento; a mayor factor “tres” mayor rendimiento del proceso.
d) ¿Cuál es la respuesta esperada en el mejor tratamiento?
r e n d im i e n t o
Gráfico de Efectos principales para rendimiento
47
45
43
41
39
37
35
-1,0
dos
1,0
-1,0
tres
1,0
 El mejor tratamiento para alcanzar el rendimiento es: cuando
se aumenta el nivel alto de los factores “dos y tres”, de esta
forma se podrá obtener un rendimiento adecuado en el
proceso.
Gráfico de Probabilidad normal para rendimiento
p o r c e n ta je
99,9 los supuestos del modelo.
e) Verifique
99
95
80
50
20
5
1
0,1
-4,1
-2,1
-0,1
1,9
3,9
Efectos estandarizados
5,9
 En este grafico podemos ver de que los puntos o residuos
están casi alineados con la línea recta; por tato, decimos de
que no hay problemas con los supuestos de normalidad.
r e s id u o s
Gráfico de residuos para rendimiento
12
8
4
0
-4
-8
-12
22
32
42
52
62
pronosticado
o
En esta grafica se puede ver de que los puntos se distribuyen
de manera aleatoria sobre la banda horizontal (sin ningún
patrón claro y contundente); por lo tanto, cumple el supuesto
de que los tratamientos tienen igual varianza.
EXPERIMENTOS DE DISEÑOS FACTORIALES 3K:
8. se desea investigar el efecto del tipo y cantidad (%) de almidón
sobre la friabilidad (%) de tabletas. Se corre un diseño 3X3 con n=4
réplicas. Los datos obtenidos se muestran a continuación.
Tipo de Almidón
Pregelatinizado
Almidón
Dextrina
20%
0,7782
0,7654
0,7592
0,7758
0,7856
0,8093
0,8126
0,8172
0,8543
Almidón (%)
30%
0,4272
0,4336
0,4552
0,4771
0,6273
0,6592
0,6692
0,6523
0,8023
40%
0,7192
0,6742
0,6892
0,7023
0,9562
0,9656
0,9656
0,9231
1,1356
0,8792
0,8723
0,8993
0,7986
0,7992
0,7827
1,1923
1,1643
1,1732
a) Escriba el modelo estadístico más apropiado para el diseño.
 Es un modelo que considera k factores con tres niveles cada
uno y tiene 3k tratamientos.
b) Obtenga el ANOVA sin desglosar y obtenga conclusiones.
Análisis de la Varianza para friabilidad
------------------------------------------------------------------------------------------------------------Fuente
Suma de Cuadrados
Gl
Cuadrado medio
F-Ratio P-Valor
-------------------------------------------------------------------------------------------------------------A: tipo de almidón
0,5694
1
0,5694
984,10
0,0000
B: almidón
0, 0878944
1
0,0878944
151,91
0,0000
AA
0,00106184
1
0,00106184
1,84
0,1867
AB
0,132132
1
0,132132
228,36
0,0000
BB
0,483702
1
0,483702
835,98
0,0000
Bloques
0,000924212
3
0,000308071
0,53
0,6639
Error Total
0,0156222
27f
0,000578601
-------------------------------------------------------------------------------------------------------------Total (corr.)
1,29074
35
R-cuadrado = 98,7897 por ciento
R-cuadrado (ajustado para g.l.) = 98,5879
por ciento
Error Estándar de Est. = 0,0240541
Error absoluto de la media = 0,0176965
Estadístico Durbin-Watson = 2,14333
(P=0,1419)
Autocorrelación residual Lag 1 = -0,117777

En este caso, 4 de los efectos tienen los p-valores inferiores a 0,05,
indicando que son estadísticamente significativos; diferentes de cero
al 95,0% de nivel de confianza.
 El estadístico R-cuadrado indica que el modelo asi ajustado explica el
98,7897% de la variabilidad en friabilidad. El estadístico R-cuadrado
ajustado, el cual es más adecuado para la comparación de números
diferentes de variables independientes, es 98,5879%.
 El efecto más importe es el tipo de almidón con un valor F-Ratio de
984,10.
c) Realice la gráfica de efectos principales y de interacción, y
destaque los aspectos más relevantes.
Gráfico de Efectos principales para friabilidad
fria b ilid a d
0,97
0,87
0,77
0,67
0,57
0,47
-1,0
1,0
tipo de almidon
20,0
almidon
40,0
 En esta grafica se aprecia de que; cuando el tipo de almidón se
encuentra en su nivel alto la friabilidad aumenta.
 Que la cantidad de almidón influye significativamente.
Gráfico de la interacción para friabilidad
friabilidad
1,19
almidon=40,0
1,09
0,99
0,89
0,79
0,69
almidon=20,0
almidon=20,0
almidon=40,0
-1,0
1,0
tipo de almidon
 Según
este
grafico
podemos
decir que existe una interacción cuando el almidón (cantidad) es 20 y
40. Por tanto decimos que la interacción existe cuando el tipo de
almidón se encuentra en su nivel bajo.
d) De la gráfica de efectos principales para el factor % de
almidón, ¿hay algún tipo de evidencia de que el efecto no sea
lineal?, argumente su respuesta.
e) Verifique supuestos a través de graficas de residuales.
p o rce n ta je
Gráfico de Probabilidad normal para friabilidad
99,9
99
95
80
50
20
5
1
0,1
12
16
20
24
28
Efectos estandarizados
32
 Según esta grafica
podemos decir de
que los no están alineados en la línea; por tanto decimos de que se
concluye de que el supuesto de normalidad no es correcto.
Gráfico de residuos para friabilidad
re s id u o s
0,06
0,04
0,02
0
-0,02
-0,04
-0,06
0,42
0,62
0,82
1,02
1,22
 Se aprecia en la
figura de qué; no
existe un patrón claro y contundente; entonces es señal de que se
cumple el supuesto de que los tratamientos realizados tienen igual
varianza.
pronosticado
f) Obtenga el ANOVA desglosado, para ello, el efecto lineal y
cuadrático debe desglosarse solo para factor % de almidón,
ya que es el único cuantitativo. Comente lo obtenido y
contrástelo con lo observado en los incisos (c y d).
Análisis de la Varianza para friabilidad
-------------------------------------------------------------------------------Fuente
Suma de Cuadrados
Gl Cuadrado medio F-Ratio P-Valor
-------------------------------------------------------------------------------A: tipo de almidón
0,5694
1
0,5694 1002,45
0,0000
B: almidon
0,0878944
1
0,0878944
154,74
0,0000
AB
0,132132
1
0,132132
232,62
0,0000
BB
0,483702
1
0,483702
851,57
0,0000
Error Total
0,0176083
31 0,000568009
-------------------------------------------------------------------------------Total (corr.)
1,29074
35
R-cuadrado = 98,6358 por ciento
R-cuadrado (ajustado para g.l.) = 98,4598 por ciento
Error Estándar de Est. = 0,0238329
Error absoluto de la media = 0,0179442
Estadístico Durbin-Watson = 2,1522 (P=0,2711)
Autocorrelación residual Lag 1 = -0,0953396
14. Se realizan un procedimiento para comparar la proporción de
palomitas de maíz que se forman (% de granos que reventaron)
con tres marcas de palomitas para horno de
microondas. Se
utilizan hornos con dos potencias diferentes y tres tiempos de
permanencia en el horno, con 2 replicas. Se obtienen los siguientes
resultados:
Marca
potencia
1
1
2
2
3
3
500
625
500
625
500
625
Tiempo
4 min
73.8, 65.5
70.8, 75.3
45.3, 47.6
66.3, 45.7
51.4, 67.7
64.0, 77.0
4.5 min
72.7, 81.9
74.1, 72.1
73.7, 65.8
79.3, 86.5
62.5, 65.0
71.5, 80.0
5 min
70.3, 91.0
78.7, 88.7
93.4, 76.3
92.2, 84.7
50.1, 81.5
82.1, 74.5
a) ¿Qué diseño se utilizo? Escriba el modelo estadístico
correspondiente:
 Se utilizo un diseño factorial mixto debido a que los factores
estudiados no tienen el mismo numero de niveles. El total de
tratamientos realizados es 36. La necesidad de utilizar este
diseño fue por su naturaleza discreta o categórica, pues los
factores tienen un número finito y distinto de niveles, y el
interés es estudiar todos los niveles.
b) Analice estos datos y obtenga conclusiones:
Análisis de la Varianza para proporción
-------------------------------------------------------------------------------Fuente
Suma de Cuadrados
Gl Cuadrado medio
Valor
-------------------------------------------------------------------------------B: potencia
455,111
1
455,111
0,0403
C: tiempo
1892,15
1
1892,15
0,0001
Error Total
3296,34
33
99,889
-------------------------------------------------------------------------------Total (corr.)
5643,6
35
F-Ratio
P-
4,56
18,94
R-cuadrado = 41,5916 por ciento
R-cuadrado (ajustado para g.l.) = 38,0517 por ciento
o
En este caso, solo dos de los efectos (potencia y tiempo)
tienen los p-valores inferiores a 0,05, indicando que son
estadísticamente significativos; diferentes de cero al 95,0% de
nivel de confianza.
o
De acuerdo al coeficiente de determinación R aj2 (ajustado)
41,5916% de la variabilidad en la proporción de palomitas de
maíz, se puede afirmar de que este valor es tan bajo, lo cual no
permite tener una buena calidad en la predicción.
o
El estadístico R-cuadrado ajustado, el cual es más adecuado
para la comparación de números diferentes de variables
independientes, es 38,0517%.
o
El error estándar de la estimación muestra la desviación
normal de los residuos para ser 9,99445. El error absoluto de
la media (MAE) de 7,56667 es el promedio del valor de los
residuos.
c) Grafique los efectos significativos e interprételos.
p ro p o rc io n
Gráfico de Efectos principales para proporcion
83
79
75
71
67
63
500,0
625,0
potencia
4,0
tiempo
5,0
 Según este grafico se puede ver que; a mayor potencia del
horno mayor será la proporción de palomitas de maíz, a mayor
tiempo también se obtendrá
una elevada proporción de
palomitas.
d) ¿Cuáles es la potencia del horno y el tiempo recomendados
para cada marca de palomitas?
p ro p o rc io n
Gráfico de Efectos principales para proporcion
83
79
75
71
67
63
1,0
3,0
marca
500,0
625,0
potencia
4,0
5,0
tiempo
e) ¿cual es el mejor tratamiento considerando los tres factores,
y cual es el porcentaje de granos reventados que se
esperarían en el tratamiento?
Gráfico de Efectos principales para proporcion
p ro p o rc io n
83
 79
De acuerdo este grafico podemos decir; de que el mejor
tratamiento es: MARCA en su nivel bajo (1), POTENCIA en su
75
nivel alto (625), TIEMPO en su alto (5); cabe mencionar de que
71
los niveles de los factores restantes se eligen con el criterio
de economía o productividad de palomitas de maíz.
67
f) ¿Cuál63de las marcas de palomitas se afecta menos (mas
1,0
3,0 500,0
625,0 4,0
5,0
robusta) debido
a
la acción
del horno
y el
tiempo?
marca
potencia
tiempo
 Según el grafico anterior podemos decir o interpretar de que la
marca (3) de palomitas s e afecta menos que las otras dos,
debito a que esta marca es más robusta en cuanto a la
potencia del horno y el tiempo, por tanto seria menor el
porcentaje de granos reventados.
g) Compruebe los supuestos de normalidad y varianza constate.
p o r c e n ta je
Gráfico de Probabilidad normal para proporcion
99,9
99
95
80
50
20
5
1
0,1
2,1
2,5
2,9
3,3
3,7
4,1
4,5
Efectos estandarizados
 Según esta grafica podemos ver de que los puntos no están alineados
en la recta horizontal principal, por tanto se concluye de que el
supuesto de normalidad no es correcto.
r e s id u o s
Gráfico de residuos para proporcion
32
22
12
2
-8
-18
-28
45
55
65
75
85
95
pronosticado
 En esta grafica podemos ver de que los puntos no están distribuidos
de manera aleatoria en banda horizontal; por lo tanto decimos de que
no se esta cumpliendo el supuesto de varianza contante, es decir que
las varianzas no son iguales.
2. EXPERIEMETOS DE DISEÑOA FACTORIALES FRACCCIONADOS 2K-P
14. considere un experimento 2 5-1con I=ABCD que fue utilizado para
investigar los efectos de cinco factores sobre el color de un
producto químico. Los factores son A= solvente/reactante, B=
catalizador/reactante, C=temperatura, D=pureza de reactante y E=
acidez del reactante. Los resultados obtenidos son los siguientes:
e=-0.63
a=2.51
b=-2.68
Abe=1.66
C=2.06
Ace=1.22
Bce=-2.09
Abc=1.93
D=6.79
Ade=5.47
Bde=3.45
Abd=5.68
Cde=5.22
Acd=4.38
Bcd=4.30
Abcde=4.05
a) Calcule los efectos y grafíquelos en Pareto y en papel normal.
¿cuales parecen significativos?
Gráfico de Pareto estandarizado para color del producto
D:pureza
AD
B:catalizador
A:solvente
AB
E:acidez
AC
CD
+
-
0
4
8
12
16
20
 En este caso, 8 de losEfectos
efectos tienen
los p-valores inferiores a 0,05,
estandarizados
indicando que son significativamente diferentes de cero al 95,0% de
nivel de confianza.

En este diagrama se puede apreciar o detectar los efectos D, AD, B,
A, AB, E, AC y CD como los más importantes o estadísticamente
significativas.
b) Obtenga el mejor análisis de varianza. ¿con cuales efectos se
esta construyendo el error?
Análisis de la Varianza para color del producto
----------------------------------------------------------------------------------------------------------------------------Fuente
Suma de Cuadrados
Gl
Cuadrado
medio F-Ratio P-Valor
----------------------------------------------------------------------------------------------------------------------------A: solvente/reactante
6,8644
1
6,8644
34,40
0,0006
B: catalizador/reactante
7,1824
1
7,1824
35,99
0,0005
D: pureza de reactante
78,1456
1
78,1456
391,56
0,0000
E: acidez de reactante
2,73902
1
2,73902
13,72
0,0076
AB
6,5025
1
6,5025
32,58
0,0007
AC
2,48062
1
2,48062
12,43
0,0097
AD
7,3441
1
7,3441
36,80
0,0005
CD
2,03063
1
2,03063
10,17
0,0153
Error Total
1,39703
7
0,199575
----------------------------------------------------------------------------------------------------------------------------Total (corr.)
114,686
15
 Lo errores se están construyendo con aquellos efectos que no están
encima de la línea de valor (pareto), en ello se pueden identificar los
siguientes efectos: “AE, BE, BD, CD, BC, C (temperatura) y DE”;
los cuales hacen un error total de 1,39703.
c o lo r d e l p ro d u c to
c) Represente gráficamente cada efecto significativo e
interprételo con detalle.
Gráfico de Efectos principales para color del producto
5
4
3
2
1
0
solvente
catalizador
pureza
acidez
 En esta figura se muestran los efectos que están activos. De esta
forma se aprecia que a mayor pureza mayor será el color del
producto; a más catalizador menor color; a mayor cantidad de
solvente mas color y a acidez alta el color será menor.
d) Determine el mejor tratamiento y la respuesta predicha por el
modelo
 Según el grafico anterior de efectos principales para color de
producto el mejor tratamiento es: SOLVENTE en su nivel alto,
CATALIZADOR en su nivel bajo, PUREZA en su nivel alto y ACIDEZ en
su nivel bajo.
e) Haga el análisis de residuos y comente los resultados:
R-cuadrado = 98,7819 por ciento
R-cuadrado (ajustado para g.l.) = 97,3897
por ciento
Error Estándar de Est. = 0,446738
Error absoluto de la media = 0,266094
Estadístico
Durbin-Watson
=
1,31127
(P=0,1735)
 El estadístico R-cuadrado indica que el modelo a si ajustado explica el
98,7819% de la variabilidad en color del producto. El estadístico Rcuadrado ajustado, el cual es más adecuado para la comparación de
números diferentes de variables independientes, es 97,3897%.
 El error estándar de la estimación muestra la desviación normal de
los residuos para ser 0,446738. El error absoluto de la media (MAE)
de 0,266094 es el promedio del valor de los residuos.
f) Si hay algún factor que no tiene ningún efecto, colapse el
diseño. ¿que diseño resulto?
 el factor que no tiene efecto es la temperatura.
1. Problema Nº 9
A continuación se muestra los datos para un diseño en bloques
al azar.
a) Completes las sumas totales que se piden en la tabla
anterior.
Bloques
Tratamie
nto
Total
bloque=
A
B
C
por
Total
por
tratamiento
1
2
3
4
3
7
4
Y.
1=14
4
9
6
Y.
2=19
2
3
3
Y. 3=8
6
10
7
Y.
4=23
Y1.=15
Y2.=29
Y3.=20
Total
global=64
b) Calcule las sumas de cuadrados correspondientes SC TRAT,
SCa, SCT y SCE.
2
SC TRAT =
2
2
2
15 +29 +20 64
−
=25.16
4
12
2
2
2
2
2
14 +19 + 8 + 23 64
SC a=
−
=42
3
12
SC T =
3 2+7 2+ 4 2+ 42 + 92+ 62 +22+ 32+ 32+ 62 +102 +72 642
−
3
12
SC T =72.66
SC E=72.66−25.16−42=5.5
c) Obtenga la tabla de análisis de varianza y anote las
principales conclusiones.
Fuente
de
variación
Tratamiento
Bloques
Error
Total
GL
SC
MC
F
P
2
3
6
11
25.1667
42.0000
5.50
72.6667
12.5833
14
0.9167
13.73
15.27
0.006
0.003
De acuerdo al ANOVA anterior se observa que para los
tratamientos se obtuvo un valor-p = 0.006 < 0.05, por lo que se
rechaza la hipótesis nula de que las medias de los tratamientos
son iguales entre sí, en cuanto al factor de bloques se puede
concluir que su valor-p = o.oo3 < 0.05, lo que nos dice que
existen diferencias entre estos.
d) Obtenga la diferencia mínima significativa (LSD)para
comparar tratamientos en este diseño en bloques.
LSD=t ∝
2
( k−1 ) ( b−1)
√
√
√
2 CM E
b
LSD=t 0.0256
2 ( 0.9167 )
4
LSD=2.44
2 ( 0.9167 )
=1.65
4
Diferencia
poblacional
µA - µB
Diferencia muestral
Decisión
|-3.5| > 1.65
Significativa
µA - µC
µB - µC
|-1,25| > 1.65
|2,25| > 1.65
No Significativa
Significativa
Por lo que se concluye que el tratamiento A es diferente del B y el
B del C.
2. Problema Nº 11
En una empresa lechera se tienen varios silos para almacenar
leche (cisternas de 60000L). Un aspecto crítico para que se
conserve la leche es la temperatura de almacenamiento. Se
sospecha que en algunos silos hay problemas, por ello, durante
cinco días decide registrar la temperatura a cierta hora.
Obviamente la temperatura de un día a otro es una fuente de
variabilidad que podría impactar la variabilidad total.
Silo
A
B
C
D
E
Día
Lunes
4.0
5.0
4.5
2.5
4.0
Martes
4.0
6.0
4.0
4.0
4.0
Miércoles
5.0
2.0
3.5
6.5
3.5
Jueves
0.5
4.0
2.0
4.5
2.0
Viernes
3.0
4.0
3.0
4.0
4.0
a) En este problema, ¿Cuál es el factor de tratamiento y cual
el factor de bloque?
El factor de tratamiento son los silos y el factor de bloque los días.
b) Suponga un DBCA, formule las hipótesis adecuadas y el
modelo estadístico.
Modelo estadístico
{
Y ij =μ+τ i +Y i + ε ij i=1,2,. .. ,k
j=1,2, … , b
Donde
Y ij
en la medición que corresponde al tratamiento i y al
bloque de j, µ es la media global poblacional,
τi
es el efecto
debido al tratamiento i, y es el efecto debido al bloque j y
el error aleatorio.
Hipótesis
H 0 : μ 1=μ2=μ3=…=μ k =μ
H A : μi=μ j para algun i ≠ j
Que también se puede expresar como:
H 0 : τ 1=τ 2=τ 3=…=τ k =0
ε ij
en
H A : τ 1 ≠ 0 para alguni
En cualquiera de estas hipótesis la afirmación a probar es que la
respuesta media poblacional lograda con cada tratamiento es la
misma para los k tratamientos y que, por lo tanto, cada respuesta
media
μ1
es igual a la media global poblacional, µ.
c) ¿Hay diferencia entre los silos?
Fuente
de
variabilidad
Tratamiento
Bloques
Error
Total
SC
GL
CM
F
Valor-p
4,46
9.76
25.84
40.06
4
4
16
24
1.115
2.44
1.615
0.69
1.51
0.246
0.609
Aquí podemos observar que el valor-p de los silos es mayor que el
valor de significancia, es decir, que el valor-p de los silos es 0.246
y el nivel de significancia es 0.05 y por lo tanto es mayor, lo que
significa que estadísticamente son iguales.
d) ¿La temperatura de un día a otro es diferente?
Por medio del problema anterior podemos observar que la
temperatura es igual porque el valor-p de los bloques es 0.609 y
el nivel de significancia es 0.05 asi que se muestra que el valor-p
del bloque es mayor que la significancia y por lo tanto las
temperaturas son iguales.
EXPERIMENTOS DE DISEÑOS FACTORIALES 3K:
7. Se cree que la adhesividad de un pegamento depende de la
presión y de la temperatura al ser aplicado. Se realiza un
experimento factorial con ambos factores fijos.
Presión
(lb/pulg2)
120
130
140
150
250
Temperatura ºF
260
270
9.60
9.69
8.43
9.98
11.28
10.10
11.01
10.44
9.00
9.57
9.03
9.80
a) Formule las hipótesis y el modelo estadístico que se desea
probar.
 Prueba de hipótesis:
H0:
ℓi =0
HA:
ℓi ≠ 0
 Condición de rechazo:
Valor-p<α
Donde: α=0.05
 Los modelos estadísticos que se desea probar es factoriales mixtos;
es decir, cuando los factores estudiados no tienen el mismo número
de niveles. En este diseño en 9 tratamientos diferentes, que
corresponden a todas las posibles maneras en que se pueden
combinar los dos factores (temperatura y presión) en tres y cuatro
niveles respectivamente.
b) Analice los datos y obtenga las conclusiones apropiadas.
Análisis de la Varianza para adhesividad
-------------------------------------------------------------------------------Fuente
Suma de Cuadrados
Gl
Cuadrado medio
P-Valor
-------------------------------------------------------------------------------AA
4,6464
1
4,6464
16,92
0,0021
Error Total
2,74582
10
0,274582
-------------------------------------------------------------------------------Total (corr.)
7,39222
11
F-Ratio
R-cuadrado = 62,8552 por ciento
R-cuadrado (ajustado para g.l.) = 59,1408 por
ciento
Error Estándar de Est. = 0,524006
Error absoluto de la media = 0,429583
Estadístico Durbin-Watson = 3,06167
(P=0,0407)
 De acuerdo a los resultados obtenidos se puede concluir de que se
rechaza la hipótesis nula y se acepta la alternativa; entonces se
puede decir de que los efectos estáticamente diferentes.
 Además se aprecia de que F 0 de “AA”; es el único que tiene un efecto
importante. Por tanto se concluye de que si hay efecto significativo
de temperaturas sobre la adhesividad.
c) ¿Se puede analizar si hay interacción entre los dos factores
controlados?
 Según el análisis realizado no hay existe la línea ni el grafico de
interacción; ya que solo existe un solo efecto significativo.