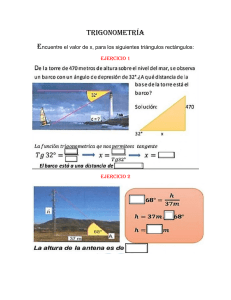
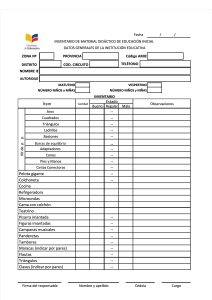
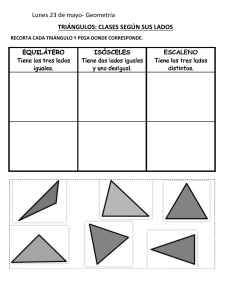
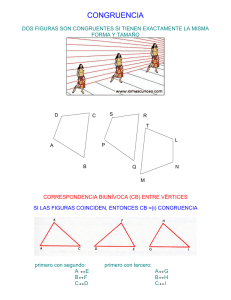
CONGRUENCIA DE TRIÁNGULOS INTRODUCCIÓN La siguiente guía de actividades busca activar los conocimientos adquiridos para el segundo periodo. Debe leer y comprender los conceptos básicos y los ejemplos de cada tema, realice un resumen o síntesis y resuelva las actividades en su cuaderno, recuerde que siempre deben aparecer los procedimientos que aplico para resolver los ejercicios. Apóyese con los videos y material que se envía por el whatsapp durante cada clase. La guía se trabajará durante 4 semanas y en cada semana se deberá enviar cada una de las actividades propuestas, según la fecha establecida. A diario se puede observar distintas formas de triángulos en techos, paredes, construcciones como puentes, edificios, casas, etc. Y muchas veces deseamos o necesitamos saber la relación que existe entre los triángulos formados en las figuras. La congruencia de triángulos es muy útil para verificar o demostrar relaciones entre diferentes figuras o entre elementos de figuras, ella se basa en el estudio de la igualdad entre triángulos, lo que permite saber si dos o más triángulos son iguales entre sí, esto es, si se comparan dos triángulos podemos saber si ellos son iguales. En esta guía veremos cómo comparar los tamaños y las formas de dos triángulos dados. Para esta comparación, se trabajará con congruencias de triángulos. Se tendrá en cuenta los requerimientos que se necesitan para verificar si dos triángulos son congruentes. 1 ¿QUÉ SABES? 2 ¡OBSERVO, LEO Y APRENDO! Dos o más figuras son congruentes si se cumple que son exactamente iguales tanto en forma como en tamaño, es decir si sus lados y sus ángulos respectivos tienen igual medida, aunque su posición y orientación sean distintas. El símbolo de congruencia es ( ≅ ). Sin embargo, para determinar que dos triángulos son congruentes, no se necesita establecer la congruencia de todos sus elementos correspondientes. Basta verificar sólo la congruencia de algunos de ellos. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes. ¡Los criterios de congruencia de triángulos proveen un atajo! Con solo 3 mediciones, a menudo podemos mostrar que dos triángulos son congruentes. Podemos dividir cualquier polígono en triángulos. Así que demostrar que los triángulos son congruentes, es también una herramienta poderosa para trabajar con figuras más complejas. Los criterios de congruencia corresponden a los postulados y teoremas que enuncian cuáles son las condiciones mínimas que deben reunir dos o más triángulos para que sean congruentes. Estas son: 3 1.- Congruencia de sus lados 2.- Congruencia de sus ángulos Para que dos triángulos sean congruentes, es suficiente que sólo algunos lados y/o ángulos sean iguales. 4 5 6 ACTIVIDADES DE APLICACIÓN Y DEMOSTRACIÓN ACTIVIDAD 1 1. Coloree del mismo color los triángulos que sean congruentes entre sí según el criterio LLL. 2. Cada par de triángulos es congruente entre sí, según el criterio LLL, entonces escriba cada proposición correctamente. Lea detenidamente el ejemplo del punto 1. 7 ACTIVIDAD 2 Utilice el criterio de congruencia de triángulos LAL para construir un triángulo congruente a cada uno de los siguientes triángulos. No olvide usar regla, compás y transportador si es necesario. 8 ACTIVIDAD 3 Escriba los segmentos o los ángulos de tal modo que se pueda concluir la congruencia entre ambos triángulos aplicando el criterio indicado. 9 ACTIVIDAD 4 Determine el criterio de congruencia para cada par de triángulos congruentes y escriba los lados y ángulos correspondientes congruentes entre sí. 10