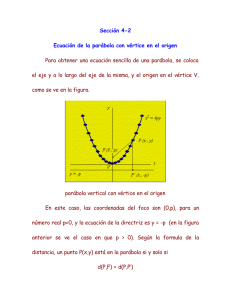
ECUACIÓN DE LA PARÁBOLA CON VÉRTICE EN V(h,k) Y CUYO EJE ES PARALELO AL EJE X. Ecuación de la parábola de este tipo es: (y – k)2 = 4𝑎 (x – h) Ecuación de la parábola en forma ordinaria Donde 𝑎 = VF (Distancia dirigida del vértice al foco) Si el foco está a la derecha del vértice entonces 𝑎 es mayor que cero y la gráfica de la ecuación es una parábola horizontal que se abre hacia la derecha. Si el foco está a la izquierda del vértice la distancia no dirigida VF en negativa, es decir 𝑎 es menor que cero, abre hacia la izquierda y su ecuación es de la forma: (y – k)2 = 4𝑎 (x – h) Ecuación de la parábola en forma ordinaria 66 Las características de la parábola son : Las coordenadas del vértice V(h,k) Las coordenadas del foco F(h + a, k) La longitud del lado recto |4𝑎| El parámetro es |2𝑎| La ecuación de la directriz es x= h - a Las coordenadas de los puntos extremos del lado recto son: (h + a, 2a) y (h + a, -2a) Ejemplo 10 Halla la ecuación de la parábola en forma ordinaria y general con vértice V(2,6) y F(2.5,6). Solución: Ejemplo 10 Como las coordenadas de y son iguales en el vértice y en el foco, significa que es una recta horizontal por lo tanto se trata de la ecuación: (y – k)2 = 4𝑎 (x – h) Ejemplo 10 Ejemplo 10 Dada las coordenadas del vértice h=2 y k=6, el valor de 𝑎 es: 𝑎 = 𝑎𝑏𝑠𝑐𝑖𝑠𝑎 𝑑𝑒𝑙 𝑓𝑜𝑐𝑜 − 𝑎𝑏𝑠𝑐𝑖𝑠𝑎 𝑑𝑒𝑙 𝑣𝑒𝑟𝑡𝑖𝑐𝑒 𝑎 = 2.5 − 2 = 0.5 (y – 6)2 = 4(0.5) (x – 2) (y – 6)2 = 2 (x – 2) Forma ordinaria de la parábola La ecuación en forma general desarrollamos el binomio al cuadrado y efectuamos la multiplicación nos queda: y2 -12y + 36 = 2x - 4 y2 -12y - 2x + 36 +4 = 0 y2 -12y- 2x + 40 = 0 Forma general de la parábola 67 Ejemplo 11 Ejemplo 11 Halla la ecuación de la parábola en forma ordinaria y general con vértice V(-4,-3) y F(-7,-3). Solución: Como las coordenadas de y son iguales en el vértice y en el foco, significa que es una recta horizontal por lo tanto se trata de la ecuación: Ejemplo 11 (y – k)2 = 4𝑎 (x – h) Dada las coordenadas del vértice h=-4 y k=-3, el valor de 𝑎 Ejemplo 11 es: 𝑎 = 𝑎𝑏𝑠𝑐𝑖𝑠𝑎 𝑑𝑒𝑙 𝑓𝑜𝑐𝑜 − 𝑎𝑏𝑠𝑐𝑖𝑠𝑎 𝑑𝑒𝑙 𝑣𝑒𝑟𝑡𝑖𝑐𝑒 𝑎 = −7 − (−4) = −7 + 4 = −3 (y + 3)2 = 4(−3) (x + 4) (y + 3 )2 = -12 (x + 4) Forma ordinaria de la parábola La ecuación en forma general desarrollamos el binomio al cuadrado y efectuamos la multiplicación nos queda: y2 + 6y + 9 = -12x - 48 y2 + 6y +12x + 9 +48 = 0 y2 + 6y+12x + 57 = 0 Forma general de la parábola Halla la ecuación de la parábola en forma ordinaria y general con vértice V(-4,-3) y 68 F(-7,-3). Solución: Como las coordenadas de y son iguales en el vértice y en el foco, significa que es una ECUACIÓN DE LA PARÁBOLA CON VÉRTICE EN V(h,k) Y CUYO EJE ES PARALELO AL EJE Y. Ecuación de la parábola de este tipo es: (x – h)2 = 4𝑎 (y – k) Ecuación de la parábola en forma ordinaria Donde 𝑎 = VF (Distancia dirigida del vértice al foco) Si el foco está hacia arriba del vértice entonces 𝑎 es mayor que cero y la gráfica de la ecuación es una parábola horizontal que se abre hacia arriba. Si el foco está hacia abajo del vértice la distancia no dirigida VF en negativa, es decir 𝑎 es menor que cero, abre hacia abajo. Las características de la parábola son: Las coordenadas del vértice V(h,k) Las coordenadas del foco F(h, k + 𝑎) La longitud del lado recto |4𝑎| El parámetro es |2𝑎| La ecuación de la directriz es y= k - 𝑎 Las coordenadas de los puntos extremos del lado recto son: (h + 2a, k) y (h - 2a, k) 69 Ejemplo 12 Ejemplo 12 Determina la ecuación en la forma ordinaria y en la forma general de la parábola con vértice en el punto V(4,3) y foco F(4,4). Solución: En este caso podemos ver que las coordenadas de x son iguales en ambos casos para el vértice y para el foco, por lo tanto es una parábola vertical. Ejemplo 12 (x – h)2 = 4𝑎 (y – k) 𝑎 = 𝑜𝑟𝑑𝑒𝑛𝑎𝑑𝑎 𝑑𝑒𝑙 𝑓𝑜𝑐𝑜 − 𝑜𝑟𝑑𝑒𝑛𝑎𝑑𝑎 𝑑𝑒𝑙 𝑣𝑒𝑟𝑡𝑖𝑐𝑒 Ejemplo 12 𝑎 =4−3=1 Con el vértice V(4,3) podemos sacar que h=4 y k=3 (x – 3)2 = 4(1) (y – 3) (x – 3)2 = 4 (y – 3) Forma ordinaria de la parábola Si desarrollamos el binomio y la respectiva multiplicación nos queda: x2 - 8x +16 = 4y -12 x2 - 8x- 4y +16+12 =0 x2 - 8x- 4y +28 =0 Ecuación general de la parábola Determina la ecuación en la forma ordinaria y en la forma general de la parábola con vértice en el punto V(4,3) y foco F(4,4). Solución: 70 En este caso podemos ver que las coordenadas de x son iguales en ambos casos para el vértice y para el foco, por lo tanto es una parábola vertical.