clase-02

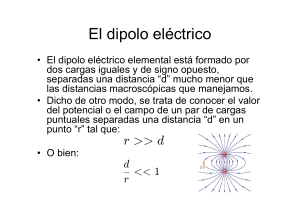
Clase 02 - Distribuciones de Carga. Campo
Eléctrico.
Prof. Juan Mauricio Matera
13 de marzo de 2019
Repaso de la clase anterior
I Cuando algunos cuerpos son frotados entre sí, adquieren la
propiedad de atraer objetos livianos, a la que llamamos
“electrización”
I Dos cuerpos del mismo material, electrizados de la misma
manera, sienten una fuerza de repulsión. Si los materiales son
distintos, pueden atraerse o repelerse dependiendo el caso.
I Dos “tipos” de electrización: “vitreos”(+) y “resinosos” (−).
Materiales con el mismo “tipo” de electrización se repelen;
materiales con distinto tipo se atraen.
I Noción de Carga Electrica (B. Franklin):
I la materia está formada por partículas “cargadas”.
I La carga puede tener dos signos, “+” y “-”.
I Un cuerpo que tiene la misma cantidad de carga “+” y carga “-”
es
I Los cuerpos se electrizan cuando ganan o pierden carga
eléctrica.
I En todo proceso, la carga neta se conserva.
I Milikan: La carga está “cuantizada”. La carga de cualquier
objeto es un múltiplo entero de 1.6 × 10−19 C.
I Thomsom, Rutherford
I La materia está formada por átomos, que se componen de un
núcleo cargado positivamente, rodeado por electrones cargados
negativamente.
I La carga de los electrones es de qe = −1.6 × 10−19 C y su masa
de me = 9.1 × 10−31 kg.
I El núcleo, está formado por protones, de carga positiva
qp = −qe , y masa mP = 1.6 × 10−27 kg y neutrones, sin carga
eléctrica, y de masa mN ≈ mP .
I En la materia no electrizada, los átomos tienen la misma
cantidad de electrones que de Protones en el núcleo, por lo que
su carga neta es nula.
I La materia adquiere carga al perder o ganar electrones.
I Los materiales pueden ser
I Conductores. Algunos de sus electrones de los átomos son
libres de moverse a través del material.
I Aislantes. Los electrones están “atados” a sus átomos.
Formas en que un material adquiere carga
I Frotamiento. Entre materiales aislantes, los electrones pasan de
un material al otro por contacto.
I Contacto. Un material conductor adquiere carga al ponerse en
contacto con un cuerpo cargado.
I Inducción. En presencia de un cuerpo cargado, un conductor
adquiere carga sin mediar contacto. Las cargas “escapan” a
tierra.
Ley de Coulomb
F~21 =
kq1 q2 ~r2 − ~r1
|~r2 − ~r1 |2 |~r2 − ~r1 |
I La fuerza entre dos cuerpos cargados distantes es proporcional
a sus cargas.
I La intensidad de la fuerza es inversamente proporcional al
cuadrado de la distancia entre los cuerpos.
I La dirección de la fuerza yace sobre la linea que une las cargas.
I Cargas del mismo signo se repelen.
I La fuerza que la carga (1) le hace a la carga (2) es igual en
magnitud y dirección, y de sentido opuesto a la que (2) le hace
a (1): Principio de acción y reacción.
Principio de superposición
La fuerza neta que un conjunto de cargas qi ejerce sobre una carga
~ i que cada carga ejerce
Q es igual a la resultante de las fuerzas F
sobre Q.
~
F
=
X
=
X
~fi
i
i
kQqi ~rQ − ~ri
|~rQ − ~ri |2 |~rQ − ~ri |
Distribuciones de cargas
Distribuciones de cargas continuas.
Si el tamaño de los objetos cargados
es comparable con la distancia de
observación, es posible
“descomponer” el objeto extendido en
objetos arbitrariamente más
pequeños. Asumimos entonces que la
carga δq de un elemento de volumen
δR en torno a un punto ~ri es
proporcional al “tamaño” del
elemento: dq = ρ|δR|.
La fuerza que sentirá una carga Q
ubicada en ~r será entonces
~Q =
F
X kQdq
i
|~r − ~ri
|2
~r − ~ri
|~r − ~ri |
En el límite |δR| → 0
~Q = Q
F
0
0
Z
R
~r − ~r kρ(~r )|dR|
|~r − ~r 0 | |~r − ~r 0 |2
Si la región es tridimensional,
|dR| = d 3 r 0 = dxdydz, por lo que la
fuerza resultante resulta ser una integral
triple de un vector:
~Q = Q
F
ZZZ
= kQ
0
0
0
0
~r − ~r kρ(~r )dx dy dz
|~r − ~r 0 |2
|~r − ~r 0 |2
X
µ=x ,y ,z
ZZZ
ûµ
0
0
0
0
0
(~r − ~r ) · ûµ kρ(~r )dx dy dz
|~r − ~r 0 |
|~r − ~r 0 |2
0
Distribuciones de carga lineales, superficiales y
volumétricas
Lineales
Superficiales
λ: Densidad lineal
de carga (C/m)
σ: Densidad
superficial de carga
(C/m2 )
Volumétricas
ρ: Densidad
volumétrica de
carga (C/m3 )
Valores típicos de la densidad de carga en diferentes
sistemas
Algunos valores típicos para la densidad superficial de carga
Medio
σ (µC/m2 )
Superficie cable
Vidrio Frotado
Van der Graff
Fotocopiadora
Nube de Tormenta
1 × 10−4
0, 01
0, 1
1
1
Relámpago λ = 0, 1C/m “. . . 1,21
Gigawatts!”
Nube de tormenta ρ = 0, 1µC/m3
Interior de un átomo ρ ≈ −1010 C/m3
Distribuciones de cargas continuas vs discretas
Si el sistema de cargas fuente está compuesto
por un gran número de cargas pequeñas,
distribuidas sobre una cierta región R, es
conveniente expresar la resultante de fuerzas en
términos de una integral:
~
F
=
X
i
~fi ≈
Z
R
~ =
dF
Z
R
kQρ(~r ) ~rQ − ~r 3
d ~r
|~rQ − ~r |2 |~rQ − ~r |
donde ρ(~r ) es la carga por unidad de
volumen en torno al punto ~r .
Distribuciones de carga 1D
En algunos casos, podemos asumir que
la carga se encuentra distribuída sobre
una curva, esto es, una región de sección
despreciable en el problema. En tal caso,
~Q = Q
F
Z
C
~r − ~s λ(~s )
|d~s |
|~r − ~s | |~r − ~s |2
donde ~s es una parametrización de la
curva C, esto es, una función que recorre
la curva C para diferentes valores de su
argumento.
λ(~s ) es la densidad lineal de carga y
tiene unidades de carga por unidad de
distancia (C/m).
Ejemplo 1: alambre cargado
Si C es un segmento de recta que va
desde ~r1 a ~r2 ,
I ~s (u) = ~r1 + u(~r2 − ~r1 ),
I 0<u<1
d~s
I |d~s | = | du
du| = |~r2 − ~r1 |du
|du| = du si los límites de
integración van de menor a
mayor)
Ejemplo 1: alambre cargado
Si C es un segmento de recta que va
desde ~r1 a ~r2 ,
I ~s (u) = ~r1 + u(~r2 − ~r1 ),
I 0<u<1
d~s
I |d~s | = | du
du| = |~r2 − ~r1 |du
|du| = du si los límites de
integración van de menor a
mayor)
Z 1
~r0 − (~r1 + (~r2 − ~r1 )u)
|~r2 − ~r1 |du
|~r0 − (~r1 + (~r2 − ~r1 )u)|3
0
Z 1
~r01 − ~r21 u
du con ~r01 = ~r0 − ~r1 , ~r21 = ~r2 − ~r1 ,
= kQ|~r21 |
λ(u)
|~r01 − ~r21 u|3
0
~ Q = kQ
F
λ(u)
Una elección más inteligente
para calcular estas integrales
viene de elegir el origen en la
carga Q, y el eje x paralelo a
~r2 − ~r1 :
I ~s (θ) =
a(−ûy + tan(θ)ûx ) + ~r0
I −θ1 < θ < θ2 / θ~i = ~ri .
I d~s = cosa2 (θ) ûx dθ
Una elección más inteligente
para calcular estas integrales
viene de elegir el origen en la
carga Q, y el eje x paralelo a
~r2 − ~r1 :
I ~s (θ) =
a(−ûy + tan(θ)ûx ) + ~r0
I −θ1 < θ < θ2 / θ~i = ~ri .
I d~s = cosa2 (θ) ûx dθ
=
Z θ2
a tan(θ)ûx + aûy adθ
(a/ cos(θ))3 cos2 (θ)
−θ1
Z θ2
Z θ2
kQ
kQ
ûx
λ(θ) sin(θ)dθ +
ûy
λ(θ) cos(θ)dθ
a
a
−θ1
−θ1
~ Q = kQ
F
λ(θ)
Ejemplo 2: Anillo cargado
Si C es una circunferencia de radio a
en el plano xy centrado en el origen,
I ~s (θ) = a(cos(θ), sin(θ), 0)
I −π < θ < π
I
d~s
dθ
dθ
= |a (− sin(θ), cos(θ), 0)| dθ = adθ
|d~s | =
Ejemplo 2: Anillo cargado
Si C es una circunferencia de radio a
en el plano xy centrado en el origen,
I ~s (θ) = a(cos(θ), sin(θ), 0)
I −π < θ < π
I
d~s
dθ
dθ
= |a (− sin(θ), cos(θ), 0)| dθ = adθ
|d~s | =
Si la carga Q está sobre el eje z, a una
distancia z0 del centro de la circunferencia, y λ
es uniforme,
=
Z π
(−a cos(θ), −a sin(θ), z0 )
adθ
(z02 + a2 )3/2
−π
2πkQλaz0
ûz
(a2 + z02 )3/2
~ Q = kQ
F
λ
Densidades superficiales
Si el material que soporta la carga es muy delgado, o la carga se
encuentra sobre la superficie del material (como ocurre en los
conductores). La distribución queda caracterizada por la superficie
y la densidad superficial de carga.
Las superficies se parametrizan como
funciones a valores vectoriales ~s (u, v ) de
dos parámetros. El elemento diferencial
de área d ~S es en general un vector, cuya
dirección es perpendicular al elemento que
describe, y su magnitud da la medida del
área que cubre.
d ~S =
∂~s
∂~s
×
∂u ∂v
donde ~a × ~b representa el producto
vectorial de los vectores ~a y ~b.
Superficies como colecciones de curvas
Si fijamos uno de los parámetros de ~r (u, v ), lo que obtenemos es
una curva, parametrizada por el parámetro restante. Podemos
pensar entonces a la fuerza generada por una superficie cargada
sobre una carga como una superposición de los campos que
general curvas que cubren a la superficie
Naturalmente, la densidad lineal de carga no será necesariamente
constante en estos casos.
Ejemplo 3: Disco cargado
Con esa idea, podemos evaluar la fuerza que un disco cargado, de
densidad superficial σ y radio a ejerce sobre una carga Q, como la
superposición de las fuerzas que ejercen anillos de densidad lineal de
carga dλ = σdr . Por ejemplo, en la posición z0 sobre el eje de
simetría,
~
F
=
Z a
2πkQz0 σrdr
0
|r 2 + z02 |3/2
Z a
= πkQz0 σ
0
|r 2
ûz
2rdr
ûz
+ z02 |3/2

= 2πkQσ 1 − q
|z0 |
z02 + a2


z0
ûz
|z0 |
Ejemplo 4: Superficie esférica
Consideremos una distribución superficial esférica de carga, con
densidad uniforme σ y radio a, frente a una carga Q a una distancia
z del centro del la esfera.
I ~s (θ, φ) = a(sin(θ) cos(φ), sin(θ) sin(φ), cos(θ)) = ar̂
I d ~S = a2 sin(θ)dθdφr̂
Ejemplo 4: Superficie esférica
Consideremos una distribución superficial esférica de carga, con
densidad uniforme σ y radio a, frente a una carga Q a una distancia
z del centro del la esfera.
I ~s (θ, φ) = a(sin(θ) cos(φ), sin(θ) sin(φ), cos(θ)) = ar̂
I d ~S = a2 sin(θ)dθdφr̂
~ = kQσ
F
Z πZ 2π
0 0
(z − a cos(θ))a2 sin(θ)dθdφ
ûz
((a sin(θ))2 + (z − a cos(θ))2 ))3/2
( k4πa2 σ
~ =
F
|z|2
0
ûz
zr
z<r
I Fuera de la esfera, la fuerza es como sí toda la carga del
cascarón q = 4πa2 σ estuviese en el centro de la esfera.
I Dentro de la esfera, la fuerza neta es nula, independientemente
de la posición de Q.
Distribuciones volumétricas de carga
I Las cargas se encuentran distribuídas sobre en volumen, de
manera uniforme sobre distancias que la distancia a la carga
I Sólo es posible en modelos de medios aislantes
I La fuerza resultante puede pensarse como la superposición de
contribuciones muchas distribuciones superficiales de carga.
Ejemplo 5: Fuerza debida a una distribución esférica de carga
(ejercicio).
Campo Eléctrico.
Definiciones
I Carga de prueba: una carga idealmente “puntual” (pequeña
frente a cualquier otra escala del sistema), de un valor lo
bastante pequeño como para no perturbar el equilibrio de la
distribución de cargas.
~ (~r ) que podemos asignar a
I Campo eléctrico: Es un vector E
cada punto del espacio, tal que la fuerza que siente una carga
~ δq = δq E
~ (~r )
de prueba δq, ubicada en la posición ~r satisface F
Dada una distribución de cargas, el campo eléctrico en un
punto existe independientemente de la presencia o no de una
carga de prueba
I El campo eléctrico de una carga puntual q ubicada en un punto
~r será
~ (~r ) = q(~r − ~r0 )
E
4πε0 |~r − ~r0 |3
En este punto, introducimos la constante ε0 = 8, 85pFm−1 =
llamada permitividad del vacío
1
4πk
I Por su definición, el campo eléctrico satisface el principio de
superposición lineal: El campo en presencia de dos
distribuciones de carga es la suma de los campos que
generarían las distribuciones por separado.
I El concepto de Campo es de suma
importancia en física.
I Permite describir la influencia que
uno o más cuerpos ejercen sobre el
espacio que los rodea.
I Matemáticamente, consiste en
asignar una magnitud a cada punto
del espacio: φ(~r ).
I Ejemplos
I Campo de deformación (ondas
mecánicas, escalar/vectorial )
I Campo de temperatura (escalar).
I Campo de presiones (escalar).
I Campo de velocidades (vectorial).
I Campo gravitatorio (vectorial).
¿Por qué introducir el concepto de Campo eléctrico?
El campo eléctrico nos permite separar -formalmente- el problema
de evaluar las interacciones en un sistema de cargas en dos pasos:
I Calcular el campo generado por la distribución de cargas
(excepto potencialmente aquella sobre la que queremos calcular
la fuerza.
I Calcular la fuerza que ejerce el campo sobre cada partícula.
Veremos más adelante que más allá de proveer una herramienta
matemática, conviene pensar al campo eléctrico como un ente
físico independiente, que es afectado por la presencia de cargas
eléctricas, y que a su vez afecta el movimiento de estas.
Valores típicos del campo eléctrico
El campo eléctrico se mide en Newton/Coulomb. Algunos valores
típicos típicos son
Medio
~ | (N/C)
|E
Atmósfera limpia
Vidrio Frotado
Fotocopiadora
Nube de Tormenta
Chispa en el aire
100
1 × 103
1 × 105
1 × 105
5 × 106
Valores típicos del campo eléctrico
El campo eléctrico se mide en Newton/Coulomb. Algunos valores
típicos típicos son
Medio
~ | (N/C)
|E
Atmósfera limpia
Vidrio Frotado
Fotocopiadora
Nube de Tormenta
Chispa en el aire
100
1 × 103
1 × 105
1 × 105
5 × 106
I Carga del electrón 1.6 × 10−19 C
I Carga total sobre la superficie del Van der Graff: q ≈ 10nC
Campo Eléctrico de una Carga Puntual
A partir de la Ley de Coulomb, el campo eléctrico de una carga
puntual de magnitud q, ubicada en ~r0 viene dado por
~ (~r ) =
E
~r − ~r0
q
2
4πε0 |~r − ~r0 | |~r − ~r0 |
~ (~r ) apunta en la dirección de la carga puntual que le da
I E
origen.
~ (~r ) apunta en el sentido que se aleja
I Si la carga es positiva, E
de la carga, y si es negativa, en el sentido que apunta hacia la
carga.
I La magnitud del campo cae como la inversa al cuadrado de la
distancia a la carga.
Campo Eléctrico de dos cargas puntuales: el dipolo
eléctrico
I Dipolo eléctrico (ideal): dos cargas puntuales de igual
magnitud y diferente signo separadas por una distancia
pequeña respecto a la distancia de observación.
I El campo de un dipolo eléctrico queda determinado por su
momento dipolar eléctrico definido por ~p = q(~r+ − ~r− ). El
momento dipolar eléctrico es una magnitud vectorial.
I En una distribución de carga continua, podemos definir el
momento dipolar como
Z
~p =
ρ(~r )~r dR .
R
Campo Eléctrico de dos cargas puntuales: el dipolo
eléctrico
I Dipolo eléctrico (ideal): dos cargas puntuales de igual
magnitud y diferente signo separadas por una distancia
pequeña respecto a la distancia de observación.
I El campo de un dipolo eléctrico queda determinado por su
momento dipolar eléctrico definido por ~p = q(~r+ − ~r− ). El
momento dipolar eléctrico es una magnitud vectorial.
I En una distribución de carga continua, podemos definir el
momento dipolar como
Z
~p =
ρ(~r )~r dR .
R
Veremos más adelante que el
campo eléctrico de un dipolo
puede expresarse como
~ (~r ) = 3(~p · r̂ )r̂ − ~p
E
4πε0 |~r |3
~ (~r ) = 3(~p · r̂ )r̂ − ~p
E
4πε0 |~r |3
I Simétrico respecto al eje de
simetría.
I Sobre el eje del dipolo, el
campo apunta siempre en la
dirección de ~p
I En el plano perpendicular, el
campo apunta en la
dirección opuesta a ~p
I La magnitud del campo
decae como 1/r 3 .
Aplicaciones
I El dipolo eléctrico es el modelo
más sencillo de un sistema cuya
carga neta es cero, con una
distribución de carga no trivial.
I En presencia de campos externos,
los materiales sufren
redistribuciones de cargas, que dan
lugar a momentos dipolares,
proporcionales a la intensidad del
campo externo: se polarizan.
I El torque sobre un dipolo dá
información sobre la intensidad y la
dirección del campo en el que está
inmerso. Este viene dado por
~
T~ = ~p × E